Методы оптимизации / Методы оптимизации. Методы оптимизации
Методы оптимизации
Л.А. Гладков Н.В. Гладкова
Методы оптимизации
Конспект лекций Часть 1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южный федеральный университет»
Л.А. Гладков, Н.В. Гладкова
Методы оптимизации
КОНСПЕКТ ЛЕКЦИЙ ЧАСТЬ 1
Таганрог 2012
УДК: 519.8(075)
Рецензенты:
Зав. кафедрой компьютерных образовательных технологий Санкт Петербургского государственного университета информационных технологий, механики и оптики, доктор технических наук, профессор Лисицина Л.С.;
кандидат технических наук, доцент кафедры САиТ ЮФУ Лебедев В.Б.
Гладков Л.А., Гладкова Н.В. Методы оптимизации: Конспект лекций. Ч. 1. – Таганрог: Изд во ЮФУ, 2012. – 117 с.
Рассмотрены основные определения теории оптимизации, перечислены основные типы задач оптимизации. Рассмотрены методы и алгоритмы решения обширного класса задач оптимизации задач линейного программирования. Приведена постановка задачи линейного программирования, стандартная форма и основные методы решения (графический и симплекс метод). Описана двойственная задача линейного программирования и взаимосвязь между прямой и двойственной задачами. Приведено описание отдельного класса задач линейного программирования (транспортных задач), приведена постановка транспортной задачи, методы построения начального базисного решения, а также алгоритм нахождения оптимального решения на основе метода «потенциалов». Отдельное внимание уделено методам решения задач целочисленного линейного программирования, таким как метод ветвей и границ, метод отсечений. Также приведены постановка задачи и описание основных подходов к решению задач многокритериальной оптимизации. Дано большое количество примеров решения различных задач оптимизации. Конспект лекций предназначен для студентов вузов, обучающихся по направлениям «Информатика и вычислительная техника» и «Информационные системы». Также может быть полезным для специалистов, занятых решением различных задач оптимизации и проектирования, поддержки и принятия решений, внедрения новых информационных технологий в науке, технике, образовании и экономике.
Ил. 15. Библиогр.: 8 назв.
Л.А. Гладков, 2012Н.В. Гладкова, 2012
ЮФУ, 2012
3
1.Задачи оптимизации
Всвоей жизни человек часто сталкивается с ситуацией, когда ему из некоторой совокупности возможных вариантов своего поведения или
принятия решения в какой либо области деятельности необходимо выбрать один вариант. Наилучший вариант поведения (принятие наилучшего решения) можно выбирать по разному. Если такой выбор предусматривает проведение количественного анализа ситуации путем сравнения различных вариантов с помощью какой либо количественной оценки этих вариантов, то говорят о необходимости решения задачи оптимизации (по латыни optimus наилучший). Ясно, что задача оптимизации имеет смысл, если есть несколько возможных вариантов ее решения. Эти варианты обычно называютальтернативами.
По содержанию задачи оптимизации весьма разнообразны. Они могут быть связаны с проектированием технических устройств и технологических процессов, с распределением ограниченных ресурсов и планированием работы предприятий, наконец, с решением проблем, возникающих в повседневной жизни человека. Всевозможные устройства, процессы и ситуации, применительно к которым предстоит решать задачу оптимизации, объединим общим названием объект оптимизации.
В этом разделе сформулированы некоторые основные определения и понятия, играющие важную роль в дальнейшем изложении материала, даны постановки известных и достаточно простых задач поиска экстремума из геометрии, алгебры и других разделов математики, приведены примеры прикладных задач оптимального проектирования и планирования, а также перечислены классы задач оптимизации.
1.1. Основные понятия
Обычно человек хочет сделать ―как лучше‖, но, чтобы не получить плохой результат при самых хороших намерениях, для решения задачи оптимизации нужно прежде всего найти ответы на следующие вопросы:
Что значит лучше?
Что конкретно нужно улучшить?
За счет чего можно добиться улучшения, что можно изменить?
В каких пределах можно производить изменения?
Отвечая на первый вопрос, необходимо сформулировать критерий
4
оптимальности, т.е. определить те признаки и предпочтения, по которым следует провести сравнительную оценку альтернатив и выбрать среди них наилучшую с точки зрения поставленной цели оптимизации. Именно с этой точки зрения можно ответить на второй вопрос: что конкретно нужно улучшить? Это может быть повышение производительности станка или срока службы технического устройства, снижение массы конструкции летательного аппарата или затрат на его производство и т.п.
Для ответа на два последних вопроса необходимо располагать математической моделью объекта оптимизации. Эта модель описывает объект при помощи соотношений между величинами, характеризующими его свойства. Обычно хотя бы часть этих величин можно изменять в некоторых пределах, что и порождает множество альтернатив, среди которых и предстоит выбрать наилучшую. Изменяемые при оптимизации величины, входящие в математическую модель объекта оптимизации, называютпараметрами оптимизации, а соотношения, устанавливающие пределы возможного изменения этих параметров,ограничениями. Эти ограничения могут быть заданы в форме равенств или неравенств. Их называют соответственноограничениями типа равенства илиограничениями типа неравенства.
Если множество параметров оптимизации является подмножеством конечномерного линейного пространства, то говорят о конечномерной задаче оптимизации в отличие от бесконечномерных задач, которые рассматривают в вариационном исчислении и оптимальном управлении. При этом критерием оптимальности может быть требование достижения наибольшего или наименьшего значения одной или несколькими действительными (скалярными) функциями параметров оптимизации, выражающими количественно меру достижения цели оптимизации рассматриваемого объекта. Каждую из таких функций принято называтьцелевой. Если целевая функция единственная, то задачу конечномерной оптимизации называютзадачей математического программирования, а в противном случае задачей многокритериальной (векторной) оптимизации. В дальнейшем ограничимся рассмотрением задач математического программирования и методов их решения.
Если целевая функция и ограничения являются линейными относительно параметров оптимизации, то говорят о задаче линейного программирования. Одну из первых таких задач сформулировал и решил
5
Л.В. Канторович. Задача Канторовича была связана с выбором оптимальной производственной программы, что и объясняет появление в названии этого класса задач слова ―программирование‖. При нелинейной зависимости целевой функции или ограничений от параметров оптимизации говорят о
задаче нелинейного программирования.
1.2. Примеры задач оптимизации
Начнем с рассмотрения достаточно простых задач оптимизации из геометрии, алгебры и некоторых других разделов математики. Эти задачи обычно можно решить геометрическим или алгебраическим путем, а также при помощи необходимых и достаточных условий экстремума действительной (скалярной) функции одного переменного. Включение таких примеров в эту книгу важно по нескольким причинам. Во первых, эти задачи тесно связаны с историей развития методов оптимизации и позволяют наглядно продемонстрировать многообразиеобъектов оптимизации. Во вторых, на простой задаче можно более четко выявить особенности построенияматематических моделей таких объектов с точки зрения выбранногокритерия оптимальности и проследить этапы процесса формулировкизадачи математического программирования.
В третьих, знание способов и результатов решения многих из этих задач помогает при решении более сложных задач оптимизации, например задач оптимального проектирования.
Пример 1.1
Найдем стороны прямоугольника, вписанного в окружность радиусом R и имеющего наибольшую площадьS (рис. 1.1).
Рис. 1.1
Эта задача известна с глубокой древности, и ее нетрудно решить геометрическим путем. Диагональ вписанного в окружность прямоугольника является диаметром окружности и имеет фиксированную длину. Площадь S прямоугольника равна половине произведения его диагоналей на синус углаφ между диагоналями, т.е.S = 2R2sinφ. Ясно, что эта площадь будет наибольшей приsinφ = 1, или приφ = π/2. В этом случае

6
диагонали прямоугольника перпендикулярны, а сам прямоугольник представляет собой квадрат. Таким образом, прямоугольником наибольшей площади, вписанным в окружность, является квадрат со стороной 2 и площадью 2R2.
Если в качестве параметров оптимизации выбрать длиныа ≥ 0 иb ≥ 0 сторон прямоугольника, то получимцелевую функцию S =аb иограничение a2 b2 2R типа равенства, нелинейные по отношению к этим параметрам. Поэтому рассматриваемую задачу оптимизации следует отнести к задачамнелинейного программирования. Ее математическую
формулировку можно представить в виде
S ab max;
a2 b2 4R2 ,a 0,b 0.
Эту задачу можно решить одним из известных стандартных путей: либо использовать формальную процедуру поиска условного экстремума функции S =ab двух переменных с одним уравнением связи, построив функцию Лагранжа, либо выразить при помощи ограничения одно переменное через другое и перейти к поиску экстремума функции одного переменного. Отметим, что в данном случае возможен и нестандартный способ решения, связанный с построением вспомогательного соотношения
4R2 2S =а2 +b2 2аb = (a b)2, или S = 2R2 (a b)2 . Отсюда следует, чтоS
2
достигает наибольшего значения S* = 2R2 при условииа =b, т.е. когда прямоугольник является квадратом, причема =b =R 2 .
Пример 1.2 (задача Евклида)
В заданный треугольник ABC с высотойН и основаниемb вписать параллелограмм наибольшей площади, стороны которого параллельны двум сторонам треугольника (рис. 1.2).
Рис. 1.2
Критерием оптимальности в этой задаче является достижение площадью параллелограмма наибольшего значения, а ограничения связаны с условиями параллельности сторон и размещения параллелограмма в
7
пределах заданного треугольника.
Выберем прямоугольную систему координат, совместив ее начало с общей вершиной параллелограмма и треугольника (вершина А на рис. 1.2), а ось абсцисс с одной из сторон треугольника. В качестве параметров оптимизации выберем основаниех параллелограмма и его высотуh. Тогда площадьS параллелограмма можно записать в видеS =hx, а условие, что параллелограмм вписан в треугольник, как ограничение типа равенства (Hh)/H =x/b, которое вытекает из подобия треугольниковDBE иABC. Итак, имеем задачу оптимизации
S hx max;
H h x ,h 0,x 0.
H b
Эту задачу также можно решить стандартными способами (см. пример 1.1). Ее решением является параллелограмм с основанием x* =b/2 и высотойh* = (1x/b)H = H/2. Отметим, что выбор вершины треугольника, с которой совпадает вершина параллелограмма, не является существенным, так как в любом из трех вариантов выбора вершины треугольника площадь параллелограмма максимальной площади равна половине площади треугольникаABC.
1.3. Задачи оптимального проектирования
При создании технического устройства различного назначения обычно часть его параметров можно изменять в определенных пределах. Это приводит к тому, что при проектировании появляется некоторое множество вариантов создаваемого устройства. В результате возникает проблема выбора из этого множества альтернатив наилучшей альтернативы с точки зрениякритерия оптимальности. Соответствующие такому выборузадачи оптимизации часто называют задачами оптимального проектирования.
Пример 1.3
Одной из наиболее простых задач оптимального проектирования является выбор размеров емкости определенной формы, имеющей наибольший объем при заданной площади поверхности или же наименьшую площадь при заданном объеме.
Пусть требуется спроектировать бак горючего в виде прямого кругового цилиндра заданного объема V, на изготовление которого будет затрачено

8
наименьшее количество листовой стали. В качестве параметров оптимизации выберем радиусR и высотуН цилиндра. Тогда затраты материала на изготовление бака будет определять суммарная площадьS его боковой поверхности и двух плоских днищ. Таким образом, необходимо минимизироватьцелевую функцию S = 2πR(H +R) приограничении типа равенства πR2H =V, т.е. решитьзадачу нелинейного программирования.
Если из целевой функции при помощи ограничения исключить Н и записать ее в виде
S(R)VR VR 2R2 ,
то произведение слагаемых не будет зависеть от R, и для нахождения ее минимального значения удобно использовать то же неравенство между геометрическим и арифметическим средними значениями:
|
|
|
|
|
|
| V | V |
|
|
| V V |
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
| S(R) = |
|
|
|
|
| 2 R2 | 33 |
|
|
|
|
| 2 R2 = 33 2V 2 | = S*. | |||||||||
|
|
|
|
| R | R | R R | |||||||||||||||||||
|
| Равенство | имеет |
|
| место | только | при | равенстве | слагаемых, т.е. при | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
| V | 2 R2 , тогда | R 3 | V |
| . Учитывая ограничение, получаем | ||||||||||||||||||||
|
|
| ||||||||||||||||||||||||
| R |
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
| H* | = | V | 3 | 4V |
|
|
| = 2R*, |
| ||||||
|
|
|
|
|
|
|
|
|
|
| R2 |
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. высота оптимального бака равна его диаметру.
При изготовлении одного бака нужно учитывать, что для заготовки круглого днища площадью πR2 придется взять квадратный лист площадью 4R2, причем после раскроя оставшуюся часть листа использовать будет практически невозможно. Поэтому более обоснованно в качестве целевой
минимизировать функцию ~ = 2RH + 8R2 при прежнем ограничении
S
πR2H= V.
Тогда в результате процедуры, аналогичной рассмотренной, получим
~ |
|
|
| ~ |
|
|
| ~ |
|
| 8 ~ |
| |
|
|
| 63V 2, |
|
|
| |||||||
3 V , |
| . Если предстоит изготовить крупную партию | |||||||||||
R | S | H |
|
| R | ||||||||
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
баков, то раскрой листовой стали при заготовке днищ можно провести более рационально, располагая соседние центры днищ в вершинах правильных треугольников со стороной 2R. Тогда расход листа на каждое днище будет соответствовать площади23R2 правильного шестиугольника, описанного около окружности радиусомR. При этом следует минимизировать целевую
функцию ~ = 2RH +2 при том же ограничении. В итоге получим
S 4 3R
studfiles.net
4.7. Оптимизация. Методы оптимизации
4.7.1. Общие сведения. Терминология
Некоторые сведения об оптимизации, которые необходимо учитывать при изучении данного раздела, даны в § 1.13.
Проблема оптимальности является одной из важнейших в области конструирования и производства ЭА, так как решение этой проблемы позволяет повышать эффективность изделий и технологических процессов. Принятие тех или иных решений также не обходится без применения методов оптимизации.
Оптимизация (от лат. Optinum – наилучшее) – это процесс нахождения экстремума функции или выбор наилучшего (оптимального) варианта из множества возможных вариантов (альтернатив).
Какую бы техническую задачу ни решал конструктор или технолог, он всегда стремится получить наилучший или оптимальный ответ. Любая практически реализованная конструкция или любой технологический процесс могут рассматриваться с определенной точки зрения как оптимальные, так как имелись определенные основания для предпочтения их остальным. Однако в принципе выбор оптимального варианта является сложной и трудоемкой задачей, не решенной полностью до сих пор.
Если рассматривать задачи оптимизации в конструировании и технологии, то их можно сформулировать следующим образом.
Задача оптимизации в конструировании состоит в выборе наилучшего в некотором определенном смысле варианта технического решения из большого числа возможных вариантов.
Задача оптимизации в технологии состоит в том, чтобы наилучшим образом построить технологический процесс и определить оптимальные режимы его проведения.
При разработке конструкций ЭА и технологических процессов ее производства решается большое количество задач, из которых вытекает многообразие задач оптимизации.
Так при конструировании ЭА решаются задачи:
оптимизация параметров;
оптимизация структур по критериям минимальных массы, затрат, габаритам, числу внутренних и внешних связей, суммарной длине соединительных проводников, числу пересечений соединительных проводников, магнитным и электрическим взаимодействиям;
оптимизация конструкции модулей различных уровней по надежности, тепловому режиму, по размещению, по технологичности, по стоимости;
оптимальное резервирование с учетом ограничений по массе, габаритам, стоимости;
оптимизация требований к надежности элементов;
оптимизация количества запасных элементов;
оптимизация последовательности проверок ЭА при ограниченном времени восстановления и другие.
При разработке производственных процессов изготовления ЭА решаются задачи:
оптимизация структуры производственного процесса и его отдельных звеньев;
оптимизация использования при производстве данного изделия технологических процессов и производств;
оптимизация затрат труда, средств и времени на изготовление изделия;
оптимизация номенклатуры технологических документов, применяемых в качестве директивных;
оптимизация типовых, групповых и пр. технологических процессов;
оптимизация раскроя материалов и другие.
Прежде чем приступить к изучению математических методов оптимизации, необходимо ознакомиться с рядом понятий.
Объект оптимизации – система или изделие, подвергаемые оптимизации.
Факторное пространство – это пространство (область) Х с координатами 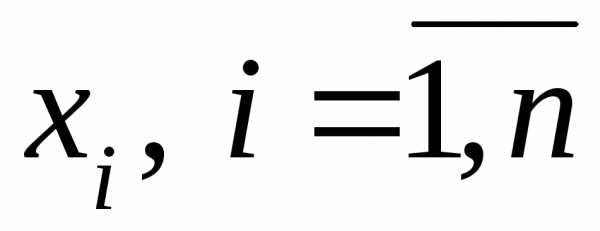 , которые соответствуют независимым переменным системы, варьируемым при исследовании.
, которые соответствуют независимым переменным системы, варьируемым при исследовании.
Функция отклика F (целевая функция) – функция, связывающая параметр оптимизации y с переменными, варьируемыми при исследовании
y = F(x1, x2, …, xn).
Поверхность отклика – геометрическое изображение функции отклика в факторном пространстве.
При изложении вопросов, связанных с поиском экстремума, полезно использовать графическое изображение поверхности отклика и траектории движения от исходной точки к экстремальной в пространстве управляемых параметров, получающейся в результате ряда последовательных шагов поиска.
Поверхность отклика функции изображают в виде совокупности линий равного уровня. Линия равного уровня – множество точек пространства, в которых рассматриваемая функция имеет одинаковые значения, равные заданной величине (при двух переменных x1 и x2). При трех переменных линии равного уровня становятся поверхностными, а при п > 3 – гиперповерхностными равного уровня (рис. 4.14)
Изображающая точка – точка в факторном пространстве, характеризующая состояние системы (в рассматриваемый момент времени).
Глобальный экстремум – это наибольшее (наименьшее) значение функции отклика F(x1,…, xn) в пределах всей области Х переменных xi (точка 01 на рис. 4.14).
Локальный экстремум – это наибольшее (наименьшее) значение функции отклика F(x1, …, xn) в некоторой точке 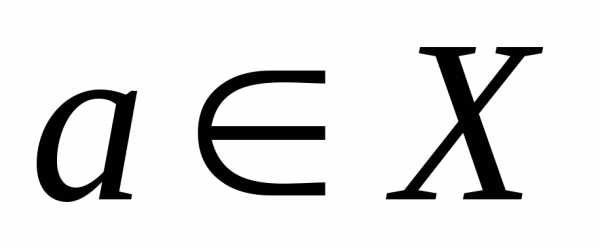 по сравнению с ее значениями в точках, принадлежащих малой окрестности точки
по сравнению с ее значениями в точках, принадлежащих малой окрестности точки (точка 02 на рис. 4.14).
(точка 02 на рис. 4.14).
Если в пределах области Х имеется всего один экстремум, то он обязательно будет глобальным.
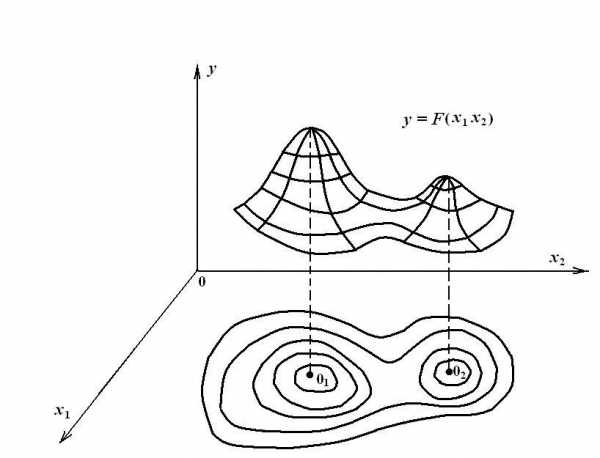
Рисунок 4.14.
Экстремум называется граничным, если он имеет место в граничных точках области Х, и внутренним, если он соответствует внутренней точке области Х.
Экстремум называется безусловным, если на переменные xi не накладывается никаких ограничений, и условным, если переменные xi связаны ограничениями типа равенств.
При оптимизации могут решаться задачи:
– задача классической оптимизации;
– задача неклассической оптимизации.
Классическая задача оптимизации заключается в оптимизации целевой функции
y = F(x1, x2, …, xn) = extr,
т.е. определяются такие значения независимых переменных (проектных параметров) xi, при которых целевая функция приобретает экстремальное значение с учетом всякого рода ограничений.
Неклассическая задача оптимизации имеет место, когда неизвестна функциональная зависимость между показателем качества (параметром оптимизации) y и параметрами xi. Поэтому в такой задаче оптимизируется не только целевая функция, но и сам способ оптимизации. Другими словами при неклассической задаче оптимизации выбирают также оптимальную стратегию поиска экстремума, а не только оптимальное значение параметра оптимизации y.
В общей структуре проектирования и изготовления электронной аппаратуры можно выделить три этапа оптимизации:
– структурная оптимизация – выбор наилучшей конструкторской реализации ЭА, обеспечивающей выполнение заданных функциональных требований;
– параметрическая оптимизация – выбор наилучшего соотношения номинальных параметров, обеспечивающих заданные электрические характеристики, и определение допусков на параметры элементов по допустимому отклонению выходных параметров;
– технологическая оптимизация – выбор номинальных значений конструкционных параметров и технологической точности на них, исходя из производственных и экономических требований.
На каждом из этапов встает проблема формулировки критерия оптимальности и оптимального решения задачи. Однако системный подход подразумевает общую оптимизацию проектирования и изготовления ЭА, так что в отдельности каждое из них может и не быть оптимальным.
Общая форма показателя оптимальности (эффективности функционирования) должна вытекать из основного постулата исследования операций: оптимальным решением является то решение, которое обеспечивает выполнение поставленной задачи при минимуме материальных затрат, либо то, которое обеспечивает выполнение поставленной задачи с максимальной эффективностью при фиксированных материальных затратах [44*].
studfiles.net
Методы оптимизации - это... Что такое Методы оптимизации?
Математическое программирование — математическая дисциплина, изучающая теорию и методы решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).
Формально, задача математического программирования формулируется так:
НайтиВ зависимости от природы множества X задачи математического программирования классифицируются как:
Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.
Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:
- Определение границ системы оптимизации
- Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
- Выбор управляемых переменных
- «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
- Определение ограничений на управляемые переменные
- … (равенства и\или неравенства)
- Выбор числового критерия оптимизации
- Создаём целевую функцию
История
Задачи линейного программирования были первыми, подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 г. Ж. Фурье и затем в 1947 г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.
Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Дж. Данцигом в 1949 г. для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях. Поэтому наименование «Математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.
Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 30-м годам ХХ столетия. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман, знаменитый математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя; советский академик, лауреат Нобелевской премии (1975 г.) Л. В. Канторович, сформулировавший ряд задач линейного программирования и предложивший (1939 г.) метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.
В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».
Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 г разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л. В. Канторовича, В. С. Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, А. Г. Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем. Методам линейного программирования посвящено много работ зарубежных ученых. В 1941 г. Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 г Дж. Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Г. Куна (англ.), А. Таккера (англ.), Гасса (Gass S. I.), Чарнеса (Charnes A.), Била (Beale E. M.) и др.
Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 г была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.
Начиная с 1955 г опубликовано много работ, посвященных квадратическому программированию (работы Била, Э. Баранкина (Barankin E.) и Дорфмана (Dorfman R.), Франка (Frank M.) и Вольфа (Wolfe P.), Г. Марковица и др.). В работах Денниса (Dennis J. B.), Розена (Rosen J. B.) и Зонтендейка (Zontendijk G.) разработаны градиентные методы решения задач нелинейного программирования.
В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.
Литература
- Хемди А. Таха Введение в исследование операций = Operations Research: An Introduction. — 8 изд.. — М.: «Вильямс», 2007. — С. 912. — ISBN 0-13-032374-8
- А.Д. Плотников Математическое программирование = экспресс-курс. — 2006. — С. 171. — ISBN 985-475-186-4
Wikimedia Foundation. 2010.
dic.academic.ru
«Методы оптимизации»
МетодЫ решения оптимизационной задачи.. 2
Методы одномерной минимизации. 2
Метод Свенна. 2
Метод золотого сечения. 2
Метод Фибоначчи. 4
Метод линейной интерполяции (метод секущих) 5
Метод средней точки (метод Больцано) 6
Метод квадратичной интерполяции – экстраполяции. 6
Метод Пауэлла. 7
Метод Давидона. 8
Методы многомерной минимизации. 9
Метод Коши. 9
Метод Циклического покоординатного спуска. 9
Метод параллельных касательных. 10
Метод Гаусса-Зейделя. 11
Метод комплексов Бокса. 11
Метод Хука-Дживса (конфигураций) 13
Метод Хука-Дживса с одномерной минимизацией. 15
Метод Ньютона. 16
Метод Зангвилла. 16
Метод Флетчера-Ривса. 17
Метод Пауэлла. 18
Курсовая работа включает в себя подавляющее большинство методов оптимизации, прочитанных в курсах «Методы оптимизации» и «Теория принятия решений». Каждый метод представлен в виде отдельной функции-члена класса. Все однотипные методы (в плане необходимых сведений для поиска) имеют одинаковое число аргументов. В большинстве своём - это начальная точка, погрешность максимальное количество шагов.
В этом разделе представлены краткие описание методов оптимизации и применяемых математических формул. Сначала идут описания одномерных методов поиска, а затем многомерных.
Методы одномерной минимизации
Метод Свенна
Метод Свенна организует начальную локализацию минимума унимодальной функции, т.е. простой одномерный поиск с удвоением шага, критерием окончания которого является появление признака возрастания функции.
Начальный этап .
(1) задать произвольную начальную точку x0 ÎRn
(2) выбрать начальный шаг h=Dx=0,01
Основной этап
Шаг 1. Установить направление убывания функции. Для этого взять x2 =x1 +h. Если f(x1 ) <f(x2 ), то поменять направление движения: h2 =-h2 и взять x2 =x1 +h2 .
Шаг 2. Вычислить fk в точках xk+1 =xk +hk , где k=2,3,4,…,m-1; hk =2hk-1 – движение с удвоением шага, до тех пор, пока не придём в точку xm такую, что f(xm )<f(xm-1 ).
Шаг 3. Установить начальный интервал локализации минимума
a1 =xm-2
b1 =xm
Метод золотого сечения
Метод золотого сечения – это процедура одномерного поиска минимума на интервале [a1 ,b1 ] или [0,1]. На каждом шаге пробная точка lk или mk внутри текущего интервала локализации [ak ,bk ] делит его в отношении, постоянном для всех интервалов
- золотое сечение. Можно показать, что , откуда , следовательно , значит . Одним из корней этого уравнения является t1 =0,618 – первое золотое число. Отметим, что t12 =0,6182 =0,382 – второе золотое число. Следует отметить, что в методе золотого сечения имеет место правило симметрии (эквидистантности) точек относительно концов интервала, а также правило одного вычисления, т.е. на каждой итерации требуется одно и только одно новое вычисление (кроме первой итерации), т.к. точки на соседних итерациях совпадают.Алгоритм ЗС-1
Начальный этап
(1) Выбрать погрешность расчёта e=10-3 ¸10-7 . Получить начальный интервал методом Свенна.
(2) Вычислить стартовые точки l1 =a1 +0,382L1 , m1 =a1 +0,618L1 (следует отметить, что золотые числа следует вычислять точно)
(3) Принять k=1 – счётчик числа итераций
Основной этап
Шаг 1.Сократить ТИЛ рассмотрением 2-х ситуаций:
(1) Если f(l)<f(m),то
ak+1 =ak
bk+1 =mk
mk+1 =lk
lk =ak+1 +0,382Lk+1
иначе
ak+1 =lk
bk+1 =bk
lk+1 =mk
mk =ak+1 +0,618Lk+1
(2) Положить k=k+1, Lk+1 =|bk+1 -ak+1 |
Шаг 2. Проверить критерий окончания поиска: если |ak+1 -bk+1 |£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как
. Иначе вернуться на шаг 1.Алгоритм ЗС-2
Начальный этап
(4) Выбрать погрешность расчёта e=10-3 ¸10-7 . Получить начальный интервал методом Свенна.
(5) Вычислить стартовые точки l1 =a1 +0,382L1 , m1 =a1 +0,618L1 (следует отметить, что золотые числа следует вычислять точно)
(6) Принять k=1 – счётчик числа итераций
Основной этап
Шаг 1. Взять очередную пробную точку x2 =ak +bk -x1 , симметричную исходной и сократить ТИЛ рассмотрением 4-х возможных ситуаций:
(1) Если (x1 <x2 ) и (f(x1 )<f(x2 )) то b=x2 ;
(2) Если (x1 <x2 ) и (f(x1 )>=f(x2 )) то a=x1 ;
(3) Если (x1 >x2 ) и (f(x1 )<f(x2 )) a=x2 ;
(4) Если (x1 >x2 ) и (f(x1 )>=f(x2 )) b=x1 ;
Увеличить счётчик числа итераций k=k+1
Шаг 2. Проверить критерий окончания поиска: если |ak+1 -bk+1 |£e - остановиться – минимум найден. Точнее фиксируем аппроксимирующий минимум как
. Иначе вернуться на шаг 1.Метод Фибоначчи
Метод Фибоначчи является процедурой линейного поиска минимума унимодальной функции f(x) на замкнутом интервале [a, b], отличающейся от процедуры золотого сечения тем, что очередная пробная точка делит интервал локализации в отношении двух последовательных чисел Фибоначчи. Последовательность чисел Фибоначчи задаётся условиями F0 = F1 = 1, Fk+1 = Fk + Fk-1 , k = 1,2,... Начальными членами последовательности будут 1, 1, 2, 3, 5, 8, 13,... Стратегия поиска Фибоначчи требует заранее указать n - число вычислений минимизируемой функции и e - константу различимости двух значений f(x). Рассмотрим один из возможных вариантов метода.
Алгоритм Фибоначчи-1
Начальный этап
(1) Задать константу e, начальный интервал [a1 , b1 ], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1 )/Ln .
(2) Взять две пробные точки l1 = a1 + (Fn-2 /Fn )(b1 - a1 ) и m1 = a1 + (Fn-1 /Fn )(b1 -a1 ). Положить k = 1.
Основной этап
Шаг 1. Сократить текущий интервал локализации:
(1) Если f(lk ) < f(mk ), то положить ak+1 = ak , bk+1 = mk ,mk+1 =lk и вычислить новую точку lk+1 = ak+1 + (Fn-k-2 /Fn-k )Lk+1 , где Lk+1 = bk+1 - ak+1 ; перейти на шаг 2.
(2) Если f(lk )>> f(mk ),то положить ak+1 =lk , bk+1 = bk , lk+1 = mk и вычислить mk+1 = ak+1 + (Fn-k-1 /Fn-k ) Lk+1 .
Шаг 2. Проверить критерий окончания поиска:
(1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1.
Шаг 3. Найти аппроксимирующий минимум х(*) :
(1) Положить mk = lk + e.
(2) Если f(lk ) > f(mk ), то x(*) = (lk + bk )/2. В противном случае - x(*) = (ak + mk )/2.
Алгоритм Фибоначчи-2
Начальный этап
(1) Задать константу e, начальный интервал [a1 , b1 ], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1 )/Ln .
(2) Выбрать одну пробную точку
. Положитьk = 1.
Основной этап
Шаг 1. Проверить критерий окончания поиска: если k=n, то остановиться и положить x*=x2 .
Шаг 2. Сократить текущий интервал локализации рассмотрением 4-х ситуаций, аналогично методу золотого сечения-2.
Метод линейной интерполяции (метод секущих)
Метод секущих предлагает заменить вторую производную f ''(xk ) в ньютоновской формуле её линейной аппроксимацией (f '(xk )-f '(xk-1 ))/(xk -xk-1 ) .
Тем самым очередное приближение хk+1 к стационарной точке х* задаётся формулой вида
xk+1 = xk - f '(xk ) * (xk - xk-1 ) / ( f '(xk ) - f '(xk-1 )).
Легко видеть, что хk+1 - точка пересечения с осью абсцисс секущей прямой, проходящей через точки хk и хk-1 .
В отличие от метода Ньютона метод секущих гарантирует сходимость точек {xk } к стационарной точке х* , однако, сходимость метода достигается ценой потери быстродейсвия. Как правило, метод дихотомии оказывается эффективнее метода секущих, хотя последний и получен из более быстродействующей схемы.
Начальный этап . Пусть методом Свенна получен интервал неопределённости [a1 ,b1 ] , границы которого удовлетворяют неравенству f'(a1 )f '(b1 ) < 0 . Задать e - погрешность вычисления минимума и принять k= 1.
mirznanii.com
Методы оптимизации - Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Оптимизация.Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Теорию и методы решения задачи оптимизации изучает математическое программирование.
Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.[1]
Постановка задачи оптимизации[ | ]
В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.
Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ*, который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:
- Допустимое множество — множество X={x→|gi(x→)≤0,i=1,…,m}⊂Rn{\displaystyle \mathbb {X} =\{{\vec {x}}|\;g_{i}({\vec {x}})\leq 0,\;i=1,\ldots ,m\}\subset \mathbb {R} ^{n}};
- Целевую функцию — отображение f:X→R{\displaystyle f:\;\mathbb {X} \to \mathbb {R} };
- Критерий поиска (max или min).
Тогда решить задачу f(x)→minx→∈X{\displaystyle f(x)\to \min _{{\vec {x}}\in \mathrm {X} }} означает одно из:
- Показать, что X=∅{\displaystyle \mathbb {X} =\varnothing }.
- Показать, что целевая функция f(x→){\displaystyle f({\vec {x}})} не ограничена снизу.
- Найти x→∗∈X:f(x→∗)=minx→∈Xf(x→){\displaystyle {\vec {x}}^{*}\in \mathbb {X} :\;f({\vec {x}}^{*})=\min _{{\vec {x}}\in \mathbb {X} }f({\vec {x}})}.
- Если ∄x→∗{\displaystyle \nexists {\vec {x}}^{*}}, то найти
encyclopaedia.bid
МЕТОДЫ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
В зависимости от природы процесса, от характера математической модели, от наличия информации о процессе, от постановки задачи применяются различные методы оптимизации процессов (табл. 22.1).
При решении конкретной задачи исследователь должен выбрать тот метод оптимизации, который при наименьших затратах на вычисления давал бы наибольший объем информации об искомом процессе.
Таблица 22.1
| Методы оптимизации | Характер процесса |
| I. Аналитические методы: аналитический поиск экстремума метод множителей Лагранжа вариационные методы принцип максимума Понтрягина | Детерминированные процессы, описываемые дифференцируе- мыми функциями с ограничени- ем и без ограничений |
| II. Методы математического программирования: геометрический линейный динамический | Детерминированные процессы с оптимизацией алгебраических функций |
| III.Градиентные методы | Детерминированные процессы с оптимизацией линейных и нели- нейных функций с ограничени- ем и без ограничения |
| IV. Автоматические методы с са- монастраивающимися моделями | Сложные объекты |
| V. Статистические методы: методы пассивного наблюдения (регрессионный и корреляционный методы анализа) методы активной оптимизации Метод Бокса - Уилсона и др. | Стохастические процессы |
Дадим краткую характеристику наиболее часто применяющимся методам оптимизации для детерминированных процессов. Методы исследования функций с помощью классического анализа являются наиболее известными способами решения несложных задач оптимизации.
Эти методы применяются для решения задач с известным аналитическим выражением критерия оптимальности, Приравнивая нулю производные и решая конечную систему уравнений, определяют экстремальные значения параметра оптимизации.
Метод множителей Лагранжа используется для решения таких же задач, как и задач, решаемых методом исследования функций, но при наличии ограничений на независимые переменные. Порядок системы уравнений, которые решаются при нахождении экстремумов параметра оптимизации, повышается на число ограничений. В остальном процедура поиска решений аналогична.
Методы вариационного исчисления обычно применяют для решения задач с критерием оптимальности в виде функционалов. Вариационными методами решение задачи сводится к интегрированию системы дифференциальных уравнений Эйлера второго порядка с граничными условиями. Число уравнений системы равно числу неизвестных функций.
Динамическое программирование является эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых общий критерий оптимизации является функцией критериев оптимальности, отдельных стадий.
Принцип максимума Понтрягина применяется для оптимизации процессов, описываемых системами дифференциальных уравнений. Оптимальное решение находится путем интегрирования системы дифференциальных уравнений процесса и системы вспомогательных функций с ограничением на обоих концах интервала интегрирования.
Линейное программирование используется для решения задач оптимизации с линейным выражением для критерия оптимальности и линейными ограничениями на область изменения переменных факторов. Это задача оптимального планирования производства с ограниченным количеством ресурсов, транспортные задачи и др. Универсальный алгоритм решения задач линейного программирования содержится в симплексном методе, позволяющем за конечное число операций найти оптимальное решение большинства задач.
Методы нелинейного (динамического) программирования применяют для решения задач оптимизации с нелинейными функциями параметра оптимизации с ограничениями и без ограничений на независимые переменные.
Для оптимизации стохастических процессов используются экспериментально-статистические методы. Различают пассивный и активный эксперимент. Пассивный эксперимент, или, как его часто назьюают, пассивное наблюдение, использует методы математической статистики для обработки информации с целью изучения закономерностей технологического процесса. При этом сбор исходных данных проводится на действующем объекте без введения в процесс искусственных изменений. Обработка данных с целью получения математической модели процесса проводится в основном методами классического регрессионного и корреляционного методов анализа.
Активный эксперимент основан на применении планирования эксперимента. Планирование эксперимента — это проведение эксперимента по заранее составленному плану (матрице), обладающему оптимальными свойствами. При планировании учитываются одновременно все факторы, влияющие на процесс, что позволяет выявить сразу и силу взаимодействия факторов, и резко сократить общее число опытов для определения оптимальных параметров. Как в пассивном, так и в активном эксперименте математической моделью является функция отклика, связывающая параметр оптимизации с факторами, влияющими на процесс:
При использовании статистических методов математическая модель представляется в виде отрезка ряда Тейлора. Уравнение регрессии имеет вид
где b0— свободный член уравнения регрессии; bi — линейные коэффициенты; bji— коэффициенты взаимодействия; bii— квадратичные коэффициенты.
Коэффициенты уравнения определяются методом наименьших квадратов (МНК) из условия
где N— объем выборки; уi— соответственно экспериментальное и теоретическое значения параметра оптимизации.
Похожие статьи:
poznayka.org
Методы оптимизации Определения
Методы оптимизацииОпределения
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчётов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т.п.
В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. В инженерных задачах их называют проектными параметрами, в экономических задачах параметрами плана. В качестве проектных параметров могут быть: значения линейных размеров объекта, массы объекта, температуры и т.п.
Число проектных параметров
характеризует размерность и степень сложности задачи оптимизации.
Выбор правильного решения или сравнивание двух альтернативных решений проводиться с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества).
В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет экстремум: минимум или максимум.
Целевую функцию можно записать в виде
(8.1)
Примеры целевых функций, встречающихся в экономических и инженерных расчетах: прочность или масса конструкции, мощность установки, объём выпуска продукции, стоимость перевозок грузов, прибыль и т.п.
При =1 целевая функция-функция одной переменной, её график - кривая на плоскости.
При =2 целевая функция-функция двух переменных, её график - поверхности в трёхмерном пространстве.
Целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать некоторые дискретные значения, задаваться в виде таблицы и т.п. В любом случае, она должна быть однозначной функцией проектных параметров.
Целевых функций может быть несколько.
Например, при проектировании изделий машиностроения одновременно требуется обеспечить надёжность,материалоёмкость, полезный объём или грузоподъёмность. Некоторые целевые функции могут оказаться несовместимыми. В таких случаях, необходимо вводить приоритет той или иной функции.
Задачи оптимизации можно классифицировать различными способами.
Пирумов: на 3 группы (см. стр. 57)
Турчак: на 2 типа: условие и без условия. Безусловная задача оптимизации
Состоит в отыскании и действительной функции (8.1) от действительных переменных определении соответствующих значений аргументов на некотором подмножестве - мерного пространства.
Обычно рассматриваются задачи минимизации; задачи на поиск к ним легко сводится путём замены знака целевой функции на противоположный. Условные задачи оптимизации или задачи с ограничениями - это задачи, при формулировке которых задаются некоторые условия (ограничения) на множестве . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения- равенства выражают зависимость между проектными параметрами, отражают законы природы, наличие ресурсов, финансовые требования и т.п.
В результате ограничений область проектирования , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число ограничений – равенство может быть произвольным.
(8.2) В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие, что, в свою очередь, может уменьшить размерность задачи и облегчить её решение.
Аналогично можно вводить ограничения-неравенства:
(8.3) Особенность отыскания решения при наличии ограничений: оптимальное решение может соответствовать либо локальному экстремуму функции внутри области проектирования, либо значению целевой функции на границе области.
Если же ограничений нет, то ищется оптимальное решение на всей области проектирования, т.е. глобальный экстремум. Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследования одного из разделов прикладной математики, математического - программирования.
Пример постановки задачи:
Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объёмом ; желательно израсходовать как можно меньше материала. При постоянной толщине стенок условие уменьшения расходов материала означает, что площадь полной поверхности контейнера должна быть .
Обозначим - рёбер контейнера. Следовательно, задача сводится к минимизации функции
(8.4) Эта функция в данном случае является целевой. Условие - ограничение – равенство. Оно позволяет исключить один параметр
(8.5)
Свели задачу к минимизации функции двух переменных. В результате решения будут найдены значения проектных параметров а потом .
Фактически получилась задача безусловной оптимизации для целевой функции (8.5), так как ограниченное равенство было использовано для исключения параметра .
Можно усложнить задачу, добавив дополнительные условия. Например, потребуем, чтобы данный контейнер имел длину не менее 2 метров.
Получим ограничение-нераенство на один из параметров
(8.5)
Таким образом, получаем условную задачу оптимизации: необходимо минимизировать функцию (8.4), учитывая ограничение-неравенство (8.5), найти оптимизацию значения параметров .
Одномерная оптимизация
Одномерная задача оптимизации формулируется следующим образом: Найти экстремум целевой функции , заданной на множестве , и определить значение проектного параметра , при котором целевая функция принимает экстремальное значение.
Существование решения поставленной задачи вытекает из теоремы Вейерштрасса: Всякая функция , непрерывная на [a,b], принимает на этом отрезке наименьшее и наибольшее значения, то есть на [a,b]
и :
.
Эта теорема не доказывает единственности решения. Не исключена возможность достижения равных экстремумов сразу в нескольких точках данного отрезка. Такая ситуация например имеет место для периодической функции (например ), рассматриваемой на отрезке, содержащем несколько периодов.
Простейший класс целевых функций случай дифференцируемой функции на [a,b],причём функция задана в виде аналитической зависимости ,и может быть найдено явное выражение для . Нахождение экстремумов таких функций проводят методами дифференциального исчисления, известными из высшей математики: функция может достигать своего наименьшего и наибольшего значения либо в граничных точках [a,b]; либо в точках и , которые обязательно должны быть критическими, то есть =0 в этих точках – это необходимое условие экстремума, для определения наименьшего и наибольшего значений функции на [a,b] нужно вычислить её значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; наименьшее или наибольшее из них и будет искомым значением.
Пример: Найти наименьшее и наибольшее значения функции на [1,3].
Решение: Найдём производную этой функции
Найдём критические точки:
=0
=0 =0, =2
=0[1,3]
Для анализа оставляем три точки:
=1
=2
=3
Сравнивая полученные величины, находим
Здесь уравнение =0 удалось решить непосредственно. Для более сложных видов необходимо использовать численные методы решения нелинейных уравнений.
Рассмотренный метод, основанный на вычислении производной целевой функции, требует её аналитического представления.
В других случаях, когда целевая функция задана в табличном виде или может быть вычислена при некоторых дискретных значениях аргумента, используют различные методы поиска. Они основаны на вычислениях целевой функции в отдельных точках и выбора среди них наибольшего или наименьшего значений.
Рассмотрим нахождение минимума функции на [a,b]. Предположим, что целевая функция унимодальна, то есть на данном отрезке она имеет только один минимум.
В инженерной практике встречаются именно такие целевые функции.
Погрешность приближённого решения задачи определяется разностью между оптимальным значением проектного параметра и приближением к нему .
Потребуем
(8.6)
заданное допустимое значение
Процесс решения задачи оптимизации методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределённости. В начале процесса оптимизации его длина равна , к концу она должна стать меньше , то есть оптимальное значение проектного параметра должно находиться в интервале неопределённости , причём тогда для выполнения условия (8.6) в качестве приближения к оптимальному значению можно принять любое , например: или или
В последнем ……для выполнения (8.6) достаточно выполнения неравенства
Наиболее простым способом сужения интервала неопределённости является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения.
Пусть число элементарных отрезков
- шаг разбиения
Вычислим значения целевой функции в узлах
Сравнивая полученные значения , найдём среди них наименьшее
Число можно приближённо принять за наименьшее значение целевой функции на [a,b].
Очевидно, для непрерывной , то есть близость к минимуму зависит от числа точек: с увеличением числа точек разбиения погрешность в определении стремиться к нулю.
Этот метод называется методом перебора.
Основная трудность: выбор и оценка погрешности.
Пример: Пусть начальная длина интервала неопределённости равна . Нужно добиться его уменьшения в сто раз. Этого легко достичь разбиением интервала на 200 частей.
Вычислив значения целевой функции , найдём её минимальное значение . Тогда искомым интервалом неопределённости будет .
Но можно сократить число разбиений. Сначала разобьём [a,b] на 20 частей и найдём интервал неопределённости длиной 0,1; при этом мы вычислим значения целевой функции в точках .
Теперь снова разобьём на 20 частей, получим искомый интервал длиной 0,01; причём значения целевой функции вычисляем в точках , так как в точках и значения уже найдены. Таким образом, во втором случае в процессе оптимизации произведено 40 вычислений значений целевой функции против 201 в первом случае.
То есть способ разбиения позволяет существенно уменьшить количество вычислений.
Существует ряд специальных методов поиска оптимизации решений: метод деления отрезка пополам, метод золотого сечения, метод Ньютона и так далее, позволяющие сократить объём вычислений и время поиска.
Метод золотого сечения
На первом шаге процесса оптимизации внутри [] выбираем некоторые точки , и вычисляем значения целевой функции ,.
В данном случае расположен на одном из прилегающих к отрезков: [] или [,].
[,] можно отбросить, сузив первоначальный интервал неопределённости.
Второй шаг проводим на [], где .
Нужно снова выбрать две внутренние точки, но одна из них -- осталась от предыдущего шага, поэтому достаточно выбрать точку , вычислить значение целевой функции и провести сравнение. В данном случае , находиться на отрезке []. Обозначим =, =, снова выбираем одну внутреннюю точку и повторим процедуру сужения интервала неопределённости. Процесс оптимизации продолжаем, пока .
Как мы выбираем внутренние точки на каждом ?
Пусть длина интервала неопределённости равна , а точка деления разбивает его на части и : >, = + .
Золотое сечение интервала неопределённости выбирают так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего интервала к длине большего интервала:
(8.7)
Отсюда можно найти точку деления, вычислив отношения: ;
Преобразуем (8.7) и найдём и :
или
так как нас интересует
__________________
Евклид (3в. до н. э.) выполнил задачу деления отрезка в данном отношении с помощью циркуля и линейки.
__________________
Очевидно, что интервал неопределённости можно разделить в соотношении золотого сечения двояко:
и . В данном случае имеем
; ;
;
(8.8)
аналогично,
(8.9)
Начальная длина интервала неопределённости
После первого шага оптимизации получаем новый интервал неопределённости []. Его длина с учётом (8.9)
на втором шаге оптимизации [] также делиться в соотношении золотого сечения. При этом одной из точек деления будет точка .
следует из соотношения
Вторая точка деления выбирается так же, как выбирается точка при делении [], аналогично (8.8) : .
Снова интервал неопределённости уменьшается до размера
по аналогии с (8.8) и (8.9) можно записать координаты точек деления и на -ом шаге оптимизации ()
;вычислению подлежит только одна из координат и ; другая берётся с предыдущего шага. При этом длина интервала неопределённости
(8.10)
Процесс оптимизации заканчивается при выполнении условия
В качестве приближения к оптимальному значению можно принять
= или = или
в последнем случае для достижения требуемой точности и выполнения неравенства (8.6) достаточно
klevoz.ru