§6. Классификация детерминированных задач оптимизации. Классификация задач оптимизации
Оптимизационные задачи, их классификация
Классификация задач оптимизации
Оптимизационная задача задаётся тройкой , гдеF – функция, определённая на множестве , аD – некоторое подмножество множества .
Функция F называется целевой функцией;
D – множеством допустимых решений (допустимой областью)
оптимизационной задачи;
U- пространством оптимизации.
Оптимизационная задача максимизации (минимизации) состоит в отыскании наибольшего (наименьшего) значения целевой функции F на допустимом множестве D.
Любая задача максимизации сводится к задаче минимизации.
Решить оптимизационную задачу – значит найти её оптимальное решение, либо установить неразрешимость этой задачи. Например, задача максимизации (минимизации) будет неразрешимой, если щелевая функцияF неограниченна сверху (снизу) на множестве D.
Методы решения оптимизационных задач зависят как от вида целевой функции F, так и от вида множества допустимых решения D. - оптимизируемая целевая функция, или целевой функционал , критерий качества - численно выражает степень достижения целей функционирования оптимизируемого объекта. Целевая функция представляет собой набор критериев качества, которые должны быть оптимизированы одновременно. Соответственно, приk=1 имеем задачу однокритериальной или скалярной оптимизации, а при k>1 – задачу многокритериальной или векторной оптимизации.
Вектор неизвестных может содержать одну компоненту (n=1) и тогда мы имеем задачу одномерной оптимизации, а может иметь и много составляющих (n>1) и тогда это задача многомерной оптимизации или задача оптимизации со многими переменными.
Допустимая область Dможет совпадать с пространством оптимизации (D =U), что означает отсутствие каких-либо ограничений на неизвестные. В этом случае имеем задачу безусловной оптимизации или задачу оптимизации без ограничений. Если же , то в задаче не все значения переменных допустимы, т.е. имеются некоторые ограничения на них. Соответствующая задача оптимизации называетсяусловной или задачей с ограничениями.
Пространство оптимизации Uможет совпадать с евклидовым пространством и мы получаем задачу оптимизации с непрерывными переменными.
Если переменные являются целочисленными, то соответствующая задача носит название целочисленной оптимизации. Частным случаем целочисленной оптимизации является булевая оптимизация, при которой переменные могут принимать только два значения – ноль и единица. Если при этом целевая функция принимает значения из множества вещественных чисел, то такая задача называется задачей псевдобулевой оптимизации, чтобы подчеркнуть ее отличие от случая, когда и значения функции тоже являются нулем или единицей.
Если же значение целевой функции зависит от некоторых комбинаций объектов из конечного набора, их размещения или способа упорядочения, то такие задачи называются задачами комбинаторной оптимизации.
Задачи целочисленной и комбинаторной оптимизации объединяются понятием задач дискретной оптимизации. Наконец, существуют задачи смешанной оптимизации, в которых могут одновременно присутствовать переменные всех типов. Наиболее известным случаем таких задач являются дачи смешанного целочисленного программирования с целочисленными и непрерывными переменными.
Приведем классификацию задач оптимизации с учетом конкретной формы задачи и свойств функции, входящих в ее постановку, как это сделано в работе [15]
Прежде всего целевая функция и функции, описывающие ограничения, могут быть заданы не аналитически, а в виде компьютерных программ, имитационных моделей, человеко-машинных процедур или даже как выход реальной системы. Такие задачи оптимизации называют задачами оптимизации с неявными функциями или поисковыми задачами оптимизации. Процесс оптимизации в таком случае больше похож на экспериментирование, чем на вычисление.
Если же все функции, входящие в постановку задачи, записываются в явном аналитическом виде , то соответствующая задача оптимизации называется задачей математического программирования. Чаще всего математическим программированием называют задачи оптимизации с ограничениями, подчеркивая их отличие от задач безусловной оптимизации.
В математическом программировании основными разделами являются: линейное программирование, целочисленное, выпуклое программирование.
Оптимизационная задача , в которой целевая функцияF является линейной функцией на , аD является множеством решений некоторой системы линейных уравнений и линейных неравенств от неизвестных, называетсязадачей линейного программирования. Систему линейных уравнений и неравенств, определяющую множество D , называют системой ограничений задачи линейного программирования.
Существуют более узкие постановки задачи линейного программирования – транспортная задача, задача о назначениях, задача целочисленного линейного программирования и другие.
Если целевая функция сепарабельна, т.е. изменяется независимо по каждой переменной в отдельности, а ограничения – линейны, то задача называется задачей сепарабельного программирования.
Если целевая функция квадратична, а ограничения – линейны, то задача называется задачей квадратичного программирования.
Если целевая функция выпукла, а функции-ограничения образуют выпуклую допустимую область, то соответствующая задача носит название задачи выпуклой оптимизации.
В случае функций общего вида говорят об общей задаче нелинейного программирования.
Предполагалось также, что все функции и коэффициенты, входящие в постановку задачи являются постоянными величинами, а они могут на самом деле зависеть от некоторого параметра или параметров. В таком случае нужно изучать поведение оптимального решения при изменении исходных данных задачи, разрабатывать методы, позволяющие находить оптимальный план сразу для совокупности значений параметров. Соответствующие задачи получили название параметрических задач оптимизации, а этот раздел методов оптимизации называется параметрическим программированием.
Наконец, до сих пор, опять таки неявно, предполагалось, что вся исходная информация определена однозначно. Такие задачи называются детерминированными. Такие модели могут оказаться неадекватными реальным процессам, которые могут характеризоваться неполнотой, неточностью данных, на основе которых формируется модель.
В ситуациях, когда все или некоторые параметры модели носят вероятностный характер, говорят опринятии решения в условиях риска и соответствующие оптимизационные задачи называют стохастическими, а соответствующий раздел теории – стохастическим программированием или стохастической аппроксимацией.
Однако неопределенность данных задачи может иметь и не вероятностный характер. В таких ситуациях говорят об оптимизации в условиях неопределенности. Методы решения в таких случаях основываются на теории нечетких множеств и так называемой нечеткой логике и объединяются под названием нечеткого математического программирования или нечеткой оптимизации.
studfiles.net
Классификация задач оптимизации (зо)
Одним из главных признаков классификации ЗО является детерминированность (определенность) задачи.
Определенная задача характеризуется тем, что все необходимые условия и параметры заданы с необходимой точностью. Чаще встречаются задачи неопределенные, причем неопределенность может иметь различный характер.
В частности, неопределенность может быть стохастической. Стохастическая неопределенность связана со случайными величинами, процессами, событиями. Здесь нужно применять аппарат теории вероятностей.
Важный класс – класс игровых ЗПР, которые связаны с наличием конфликта между ЛПР, которых может быть несколько или между ЛПР и «природой».
Кроме этого ЗПР могут быть статическими и динамическими.
Задачи линейного программирования
Исторически это первый класс, включенный в дисциплину «Исследование операций» (старое название ТПР). Это частный случай задач математического программирования.
Первый пример. Задача об использовании сырья.
Предположим, что на некотором предприятии можно изготовлять продукцию 2-х видов: П1 и П2 для чего необходимо использовать сырье 4-х видов S1, S2, S3, S4. запасы сырья каждого вида ограничены.
Имеем следующую таблицу.
| Вид сырья | Запас | Продукция П1 | Продукция П2 |
| S1 | b1 | a11 | a12 |
| S2 | b2 | a21 | a22 |
| S3 | b3 | a31 | a32 |
| S4 | b4 | a41 | a42 |
| Цена | с1 | c2 |
Программа – это искомый план производства. Она характеризуется вектором
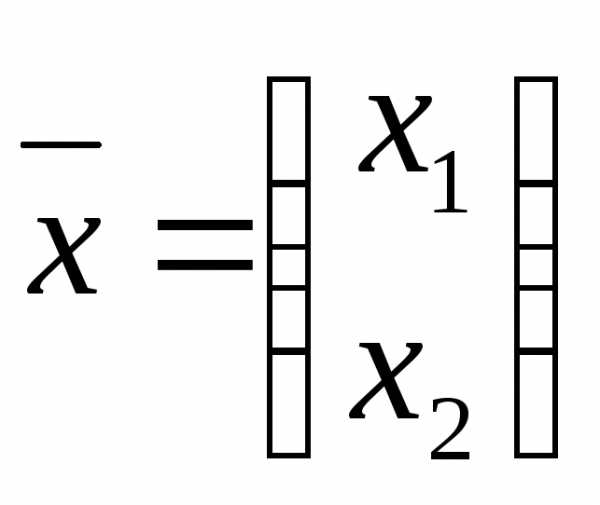 .
.
Здесь х1 – число изделий вида П1, х2 – число изделий П2, которые следует произвести по данному плану.
Если с1 и с2 цены единицы изделий вида П1 и П2 соответственно, то продав произведенную продукцию предприятие выручит сумму
Ясно, что предприятие стремиться максимизировать эту функцию.
Что ему мешает это сделать, т.е. каковы дисциплинирующие ограничения?
В таблице величина aijпредставляет собой количество сырья вида Si, которое расходуется на производство одного изделия вида Пj.
Величина biпредставляет собой запас сырья вида Si, имеющийся на складах предприятия.
Отсюда следуют дисциплинирующие ограничения
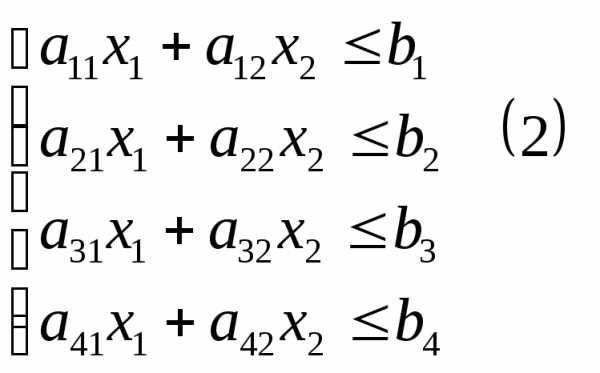
Кроме того должны выполняться естественные ограничения
Получаем следующую задачу.
Необходимо найти такой план 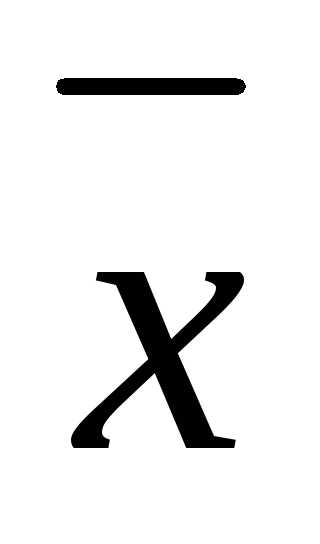 , удовлетворяющий ограничениям (2) и (3), чтобы функция (1) принимала наибольшее значение.
, удовлетворяющий ограничениям (2) и (3), чтобы функция (1) принимала наибольшее значение.
Функция (1) называется целевой функцией.
В числовом виде можно поставить такую задачу.
| Вид сырья | | П1 | П2 |
| S1 | 19 | 2 | 3 |
| S2 | 13 | 2 | 1 |
| S3 | 15 | 0 | 3 |
| S4 | 18 | 3 | 0 |
| Доход | 7 | 5 |
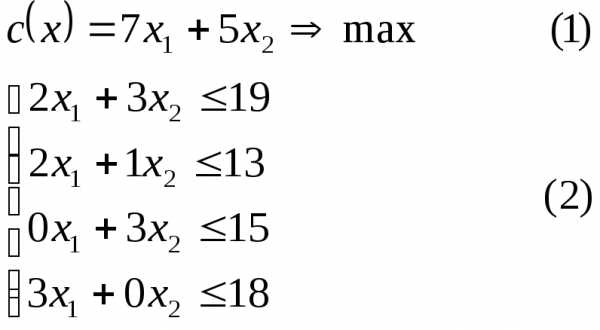
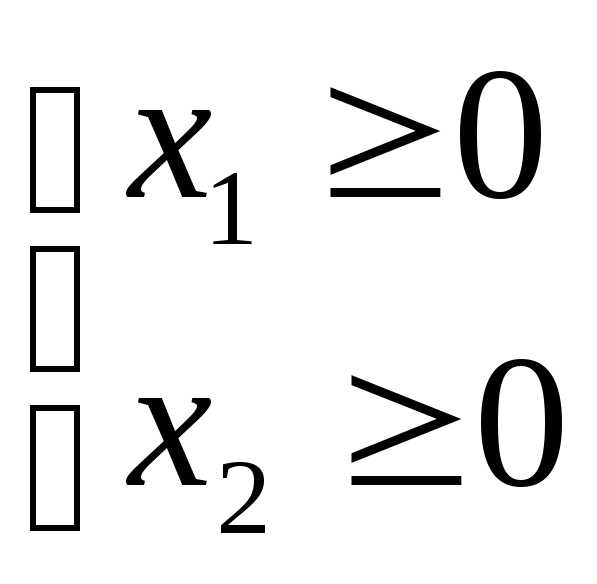

Математический смысл: необходимо найти такое неотрицательное решение системы неравенств (2), чтобы функция (1) достигала максимального значения.
Подобные задачи, в которых необходимо найти экстремум некоторой (целевой) функции при некоторых ограничениях, называются задачами математического программирования.
Если и ограничения, и целевая функция выражается с помощью линейных функций, задача называется задачей линейного программирования.
Наша задача в данном примере проста, так как неизвестных всего два (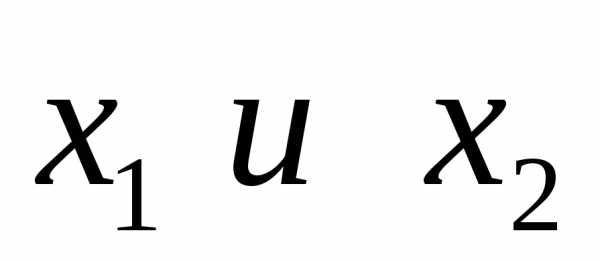 ). Поэтому решение можно провести наглядно геометрическим методом.
). Поэтому решение можно провести наглядно геометрическим методом.
Для этого в плоскости 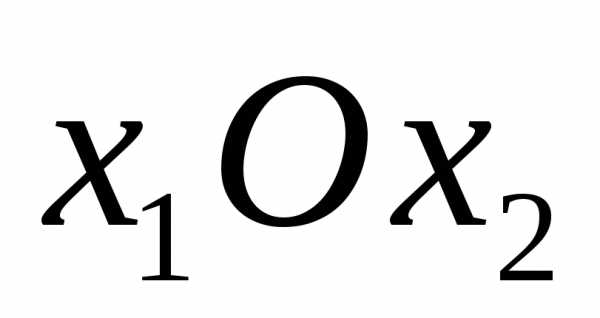 следует построить решение каждого из шести неравенств. Эти решения геометрически представляют собой полуплоскости, пересечение которых и есть решение системы ограничений (2), (3).
следует построить решение каждого из шести неравенств. Эти решения геометрически представляют собой полуплоскости, пересечение которых и есть решение системы ограничений (2), (3).
Эта область обычно бесконечна имеет вид и о всегда ограничена ломанной линией. В силу линейности функции (1). Отрезки границы являются кусками прямых, уравнения которых получаются из неравенств (2), (3) заменой символов 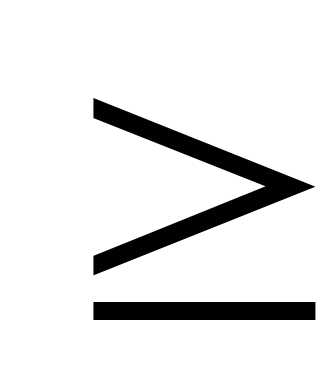 и
и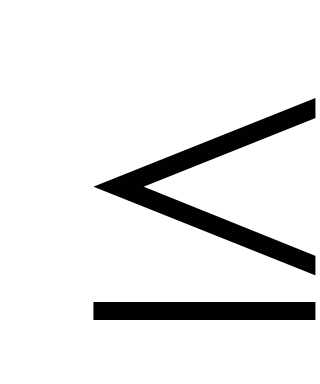 на =.
на =.
В силу линейности целевой функции (1), она вырастает в направлении градиента, который имеет координаты
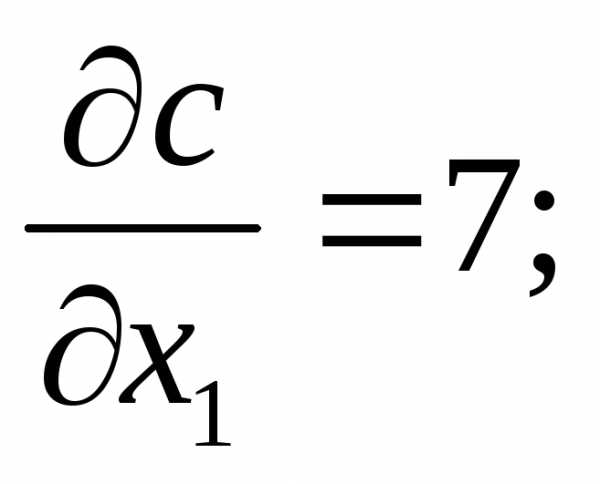
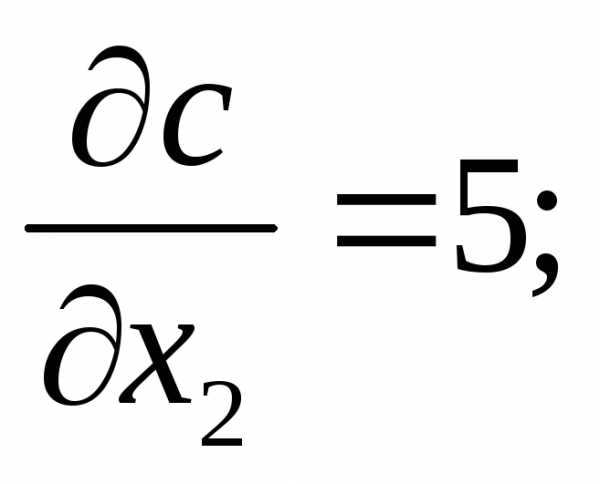
Построив какую – либо линию уровня целевой функции, например, прямую
,
следует передвигать ее в направлении градиента до крайней точки построенной области, если такая точка существует. Координаты этой точки и являются составляющими искомого оптимального плана.
Возможно, что такая точка не единственная, что свидетельствует о неоднозначности решения задачи.
Наконец, если такой точки нет, это означает , что задача не имеет решения.
ОСНОВНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ОЗЛП)
В этой ЗЛП ограничения (2) имеют вид уравнений.
Считаем, что план имеет n компонент.
Общий вид системы ограничений
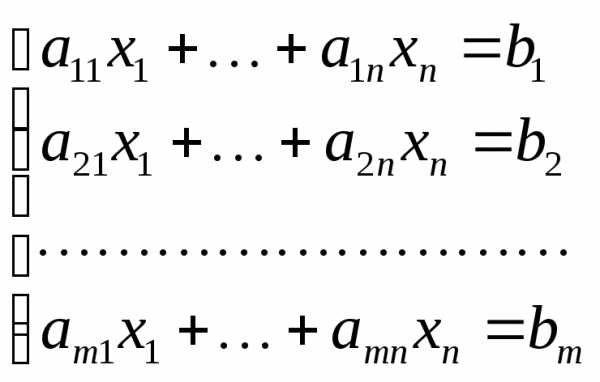
Здесь m – число уравнений – ограничений.
Целевая функция
Требуется среди всех неотрицательных решений системы (2) выбрать такое, при котором целевая функция (1) принимает минимальное значение.
Переход от максимизации к минимизации непринципиален.
Покажем, что всякая ЗЛП с ограничениями-неравенствами может быть сведена к виду ОЗЛП (правда, ценой увеличения размерности задачи)
Вернемся к системе ограничений (2) в виде неравенств. В общем случае i-е неравенство такой системы имеет вид:
Обозначим разницу между правой и левой частями этого неравенства через 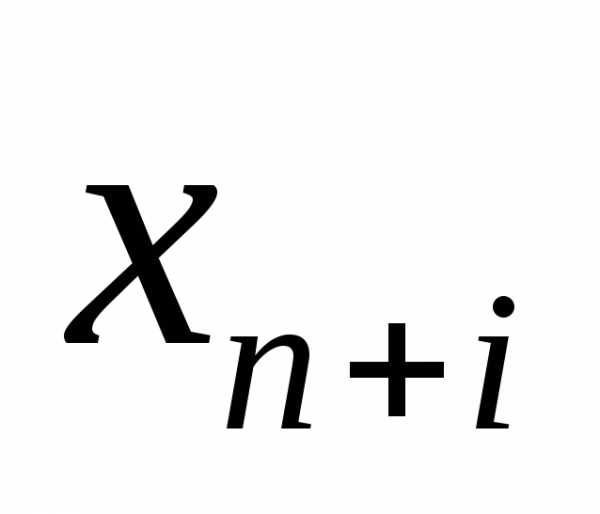 .
.
Заметим, что все новые переменные неотрицательны.
Теперь систему неравенств можно записать в виде такой системы уравнений:
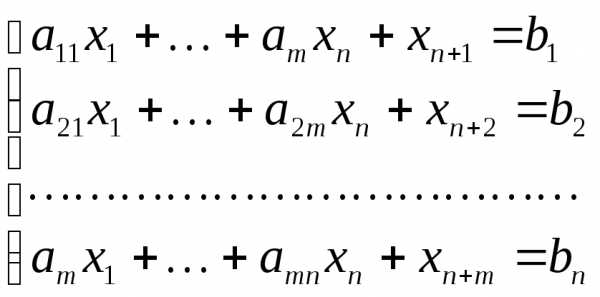
 (2/)
(2/)
Переменные 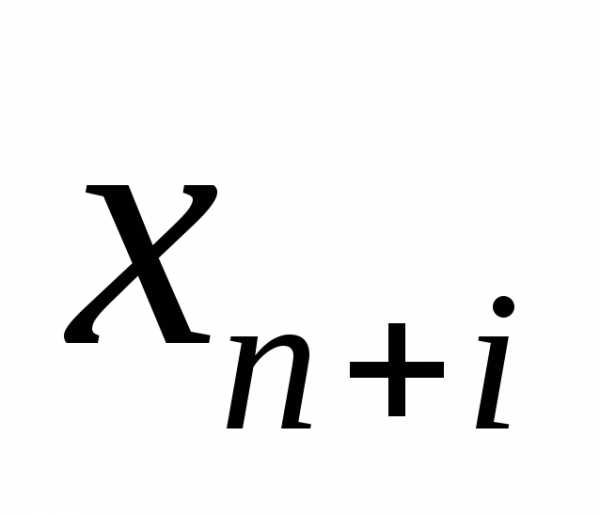 можно интерпретировать как количество сырья, оставшееся на складе после выполнения плана. При этом мы не будем менять вид целевой функции, так как вновь введенные переменные не увеличивают доход. Каждая из вновь введенных переменных неотрицательна, поэтому для них выполняются неравенства (3).
можно интерпретировать как количество сырья, оставшееся на складе после выполнения плана. При этом мы не будем менять вид целевой функции, так как вновь введенные переменные не увеличивают доход. Каждая из вновь введенных переменных неотрицательна, поэтому для них выполняются неравенства (3).
Итак, мы видим, что исходная ЗЛП с неравенствами эквивалентна некоторой ОЗЛП.
Впредь с самого начала будем считать, что задача имеет вид ОЗЛП.
Будем ее решать.
Определения.
Неотрицательное решение системы уравнений (2) называется допустимым планом.
Оптимальным планом (решением) назовем такое допустимое решение, для которого функция (1) достигает минимума.
Рангом матрицы назовем число r, которое обладает 2-мя свойствами:
существует минор матрицы порядка r, не равный 0;
всякий минор порядка r+1 равен 0.
Базисным минором назовем любой минор порядка r , не равный 0;
Рассмотрим базисный минор системы уравнений (2). Путем перестановки уравнений и перенумерации переменных добьемся того, чтобы он стоял в левом верхнем углу матрицы. Выбросим все уравнения, начиная с r+1 до m, т.е.оставим в системе ограничений (2) только первые r уравнений, так как остальные уравнения являются их следствиями в силу определения ранга матрицы.
Теперь систему ограничений можно переписать следующим образом:
(2а)
Здесь мы все переменные, начиная с 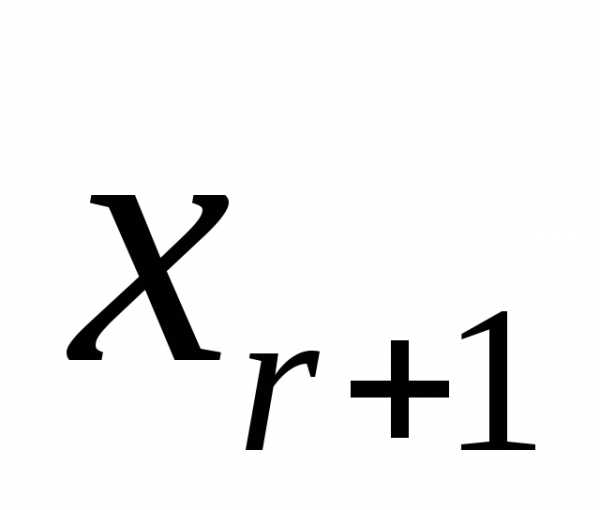 и кончая
и кончая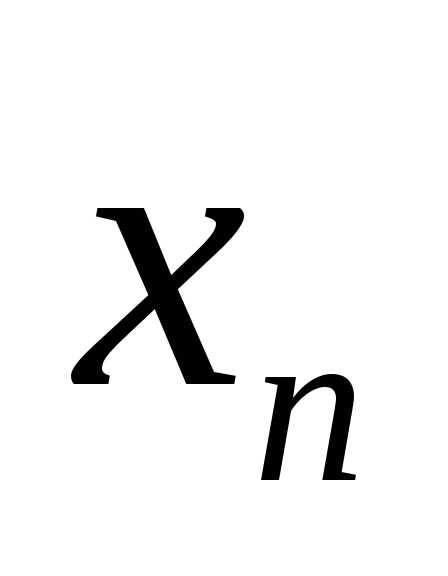 мы перенесли в левую часть уравнений системы. Рассматриваем систему (2а), как систему уравнений относительно первыхr переменных
мы перенесли в левую часть уравнений системы. Рассматриваем систему (2а), как систему уравнений относительно первыхr переменных 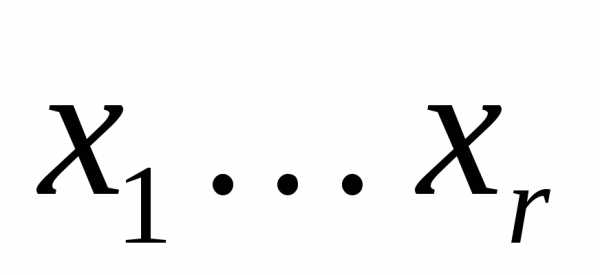
Поскольку определитель матрица этой системы есть базисный минор, то ее можно при любых 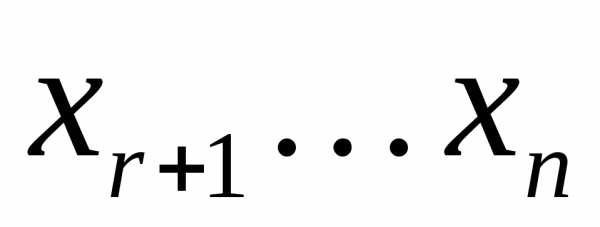 разрешить относительно
разрешить относительно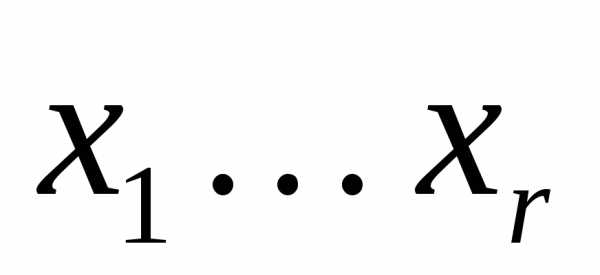 .
.
Получим систему
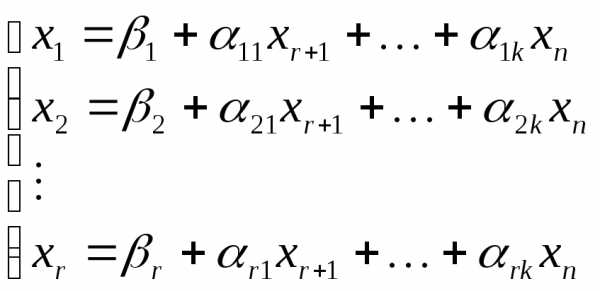 (2б)
(2б)
Здесь
Система (2б) эквивалентна системам ограничений (2) и (2а), причем записана так, что показывает структуру решений системы ограничений (2). Действительно, задав к чисел 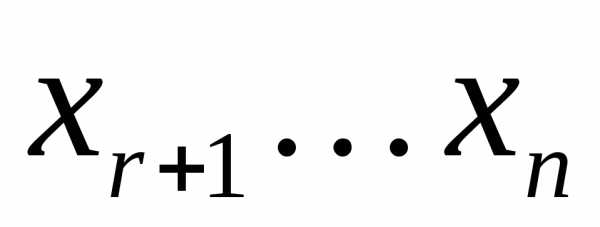 , мы получим значения и первыхr компонент соответствующего решения. Это значит, что множество решений системы (2) бесконечно, причем оно образует линейное многообразие размерности к.
, мы получим значения и первыхr компонент соответствующего решения. Это значит, что множество решений системы (2) бесконечно, причем оно образует линейное многообразие размерности к.
Назовем все переменные 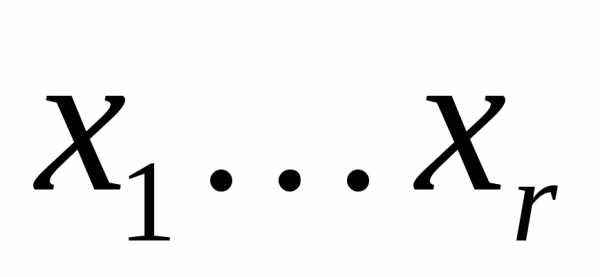 базисными, а остальные
базисными, а остальные 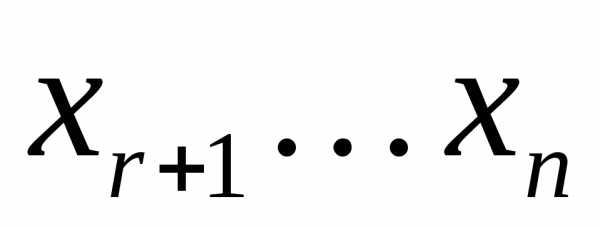 –свободными переменными. Заметим, что каждому набору значений свободных переменных
–свободными переменными. Заметим, что каждому набору значений свободных переменных 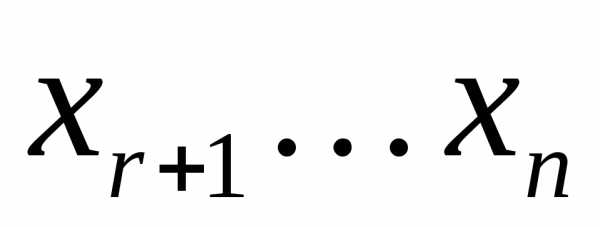 соответствует единственный набор значенийбазисных переменных
соответствует единственный набор значенийбазисных переменных 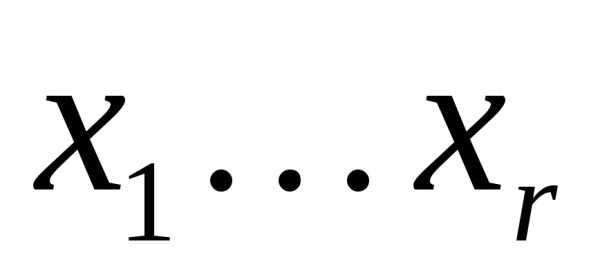 по формуле (2б) и вместе эти наборы и образуют некоторое решение из указанного многообразия.
по формуле (2б) и вместе эти наборы и образуют некоторое решение из указанного многообразия.
Мы же из всех решений, которые даются формулой (2б), возьмем одно единственное, в котором все свободные переменные равны 0.

Это решение называется базисным.
Формулы (2б) соответствуют только одному выбору базисного минора, тогда как таких миноров может быть много. Поэтому каждому базисному минору соответствует своя система вида (2б), свои наборы свободных и базисных переменных и свое базисное решение. Значит можно говорить о множестве базисных решений системы ограничений (2).
На этих понятиях строится метод решения ОЗЛП -симплекс-метод (СМ)
studfiles.net
48. Постановка и классификация детерминированных задач оптимизации.
Под решением задачи понимают процесс выбора управляемых переменных  , принадлежащих допустимой области
, принадлежащих допустимой области  и обеспечивающих оптимальное значение некоторой характеристики объекта
и обеспечивающих оптимальное значение некоторой характеристики объекта 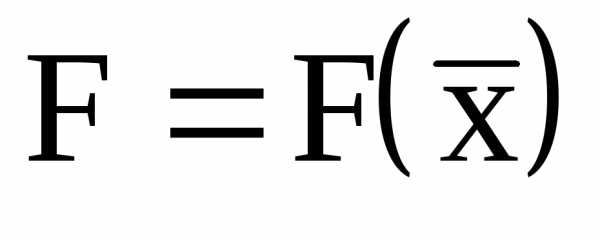 .
.
Задача называется задачей оптимизации с ограничениями или задачей условной оптимизации. Задача, в которой нет ограничений, т.е.
; называется задачей безусловной оптимизации.
Задачи, в которых  представляет собой одномерный вектор
представляет собой одномерный вектор 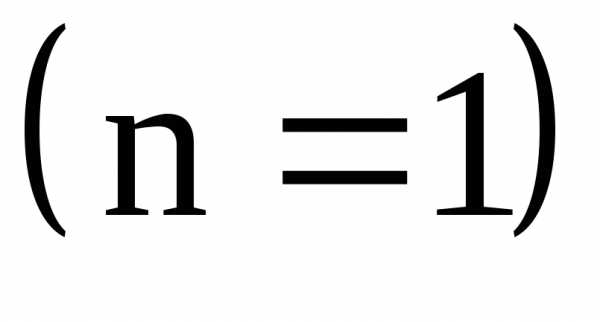 , называются задачами одномерной оптимизации. Если число варьируемых переменных больше единицы
, называются задачами одномерной оптимизации. Если число варьируемых переменных больше единицы 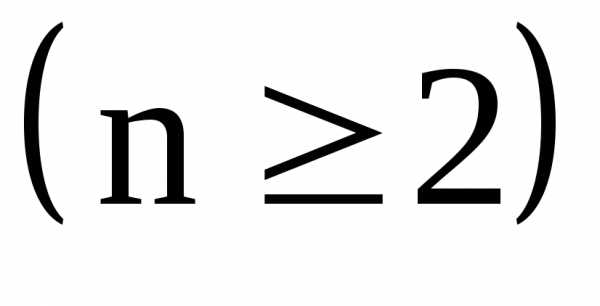 , то такие задачи являются задачами многомерной оптимизации, связанными с оптимизацией некоторой n-мерной гиперповерхности
, то такие задачи являются задачами многомерной оптимизации, связанными с оптимизацией некоторой n-мерной гиперповерхности 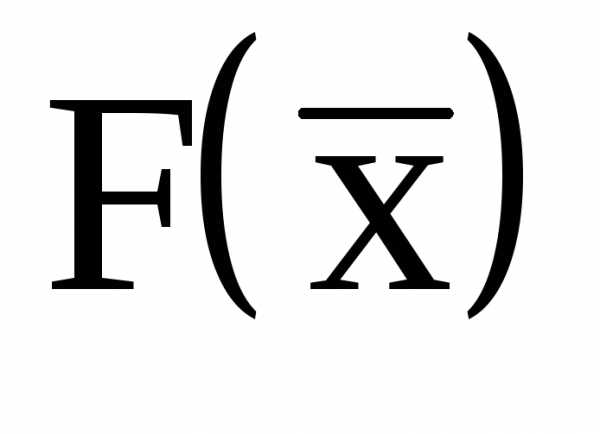
Задачи условной оптимизации, в которых функции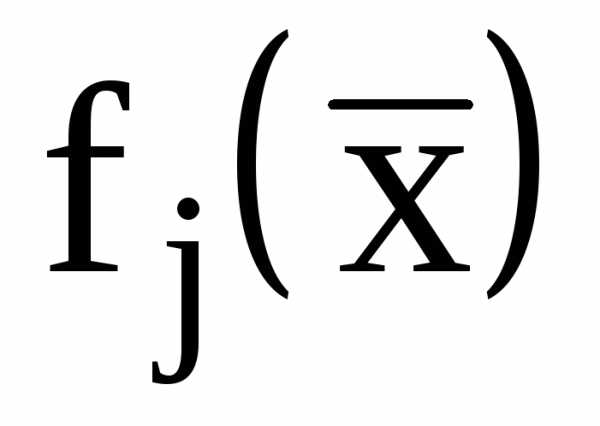 и
и 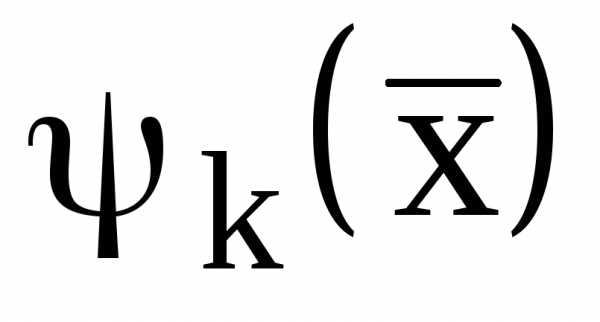 являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи с линейной целевой функцией
являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи с линейной целевой функцией 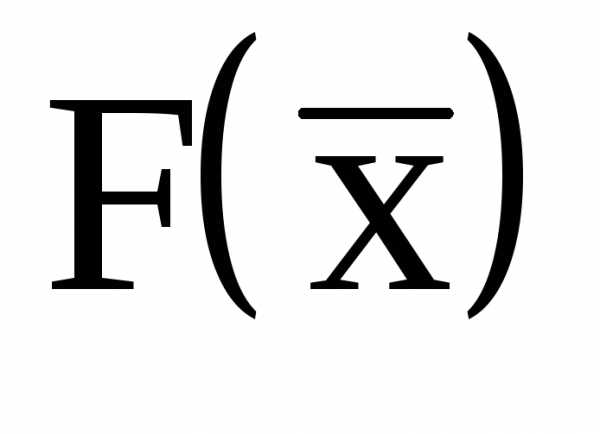 и линейными ограничениями
и линейными ограничениями 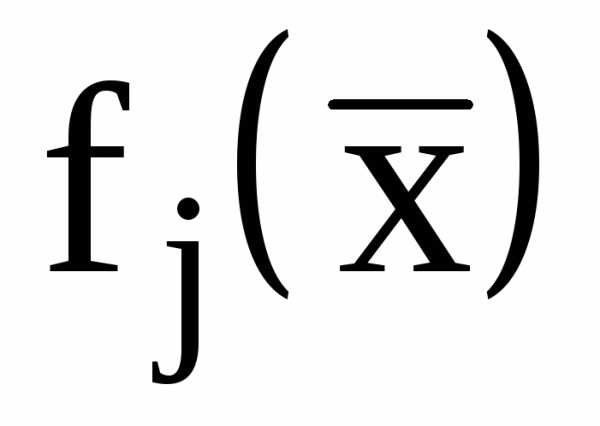 и
и 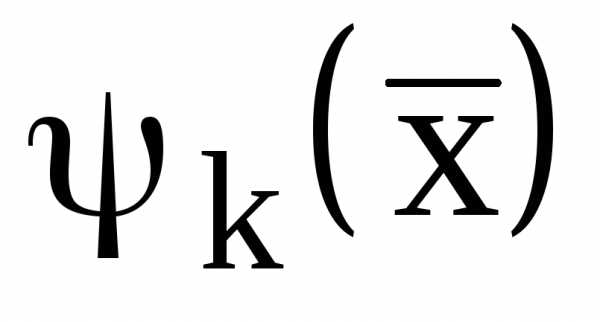 являются задачами линейного программирования (ЗЛП).
являются задачами линейного программирования (ЗЛП).
Если целевая функция 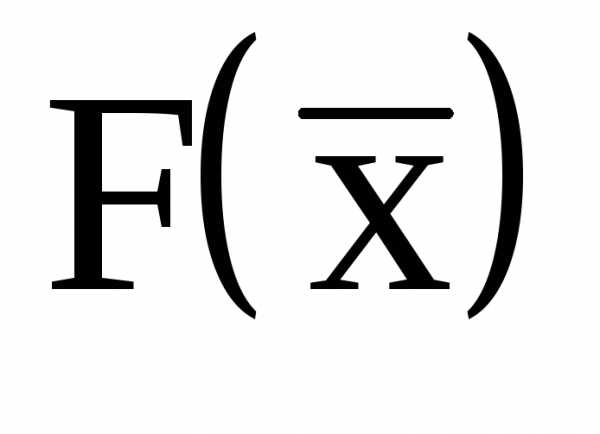 - квадратичная функция, а ограничения
- квадратичная функция, а ограничения 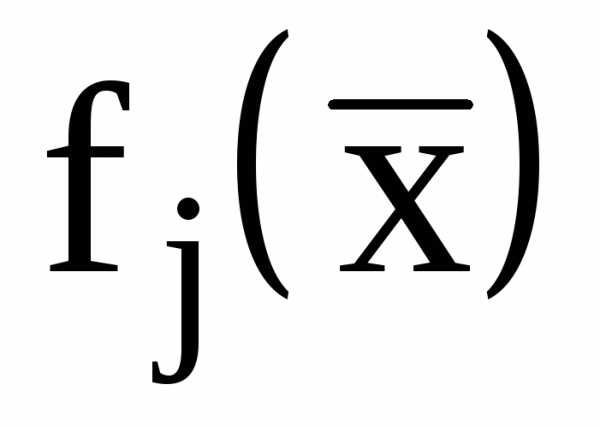 и
и 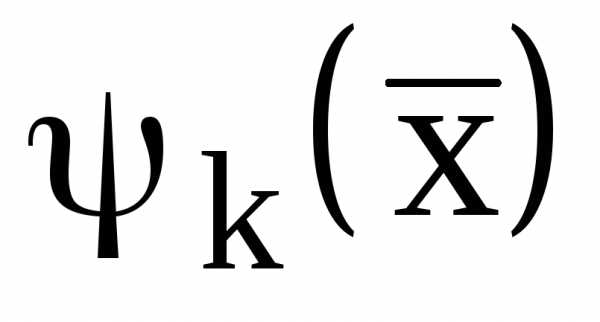 - линейные функции, то задача (1)-(4) является задачей квадратичного программирования. В тех случаях, когда критерий оптимальности
- линейные функции, то задача (1)-(4) является задачей квадратичного программирования. В тех случаях, когда критерий оптимальности 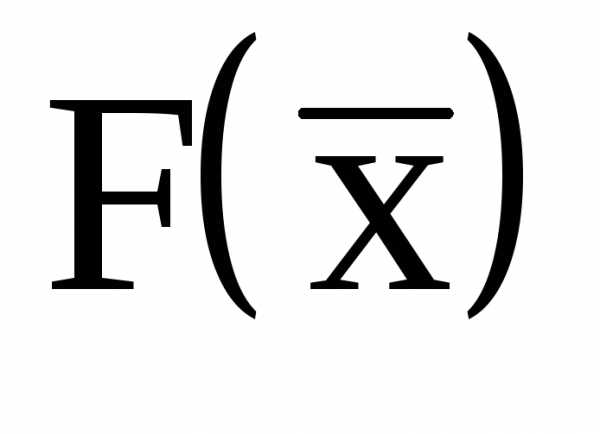 или ограничения
или ограничения 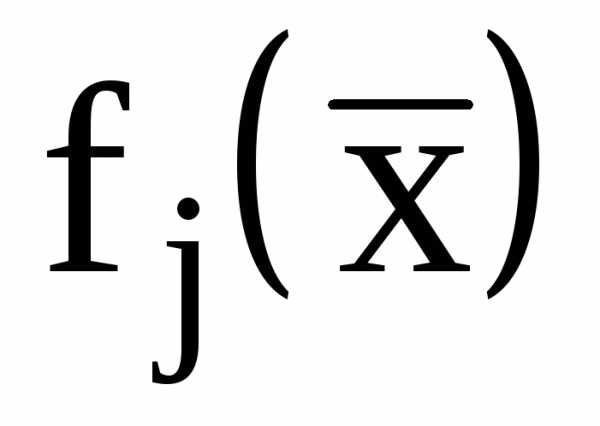 и
и 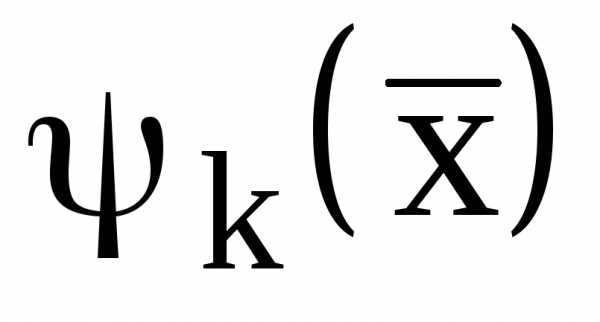 представляют собой нелинейные функции переменных
представляют собой нелинейные функции переменных  , задача (1)-(4) является задачей нелинейного программирования.
, задача (1)-(4) является задачей нелинейного программирования.
49. Многокритериальные задачи оптимизации.
В практике часто возникает необходимость найти решение, которое бы являлось наилучшим с позиций нескольких различных критериев .
Решение задачи многокритериальной оптимизации (компромиссное решение) (
 ) является эффективным решением, если для него справедливо неравенство
) является эффективным решением, если для него справедливо неравенство
,
Первый подход — выбор основного критерия. Один из путей учёта совокупности противоречивых критериев состоит в том, что какой либо из критериев выбирается в качестве основного, а остальные критерии считаются вспомогательными. Оптимизацию осуществляют по основному (одному) критерию, а на все остальные критерии накладывают ограничения.
Второй подход — ранжирование критериев. Пусть критерии ранжированы и номер критерия обозначает номер ранга. Очевидно, что оптимизацию следует начинать с критерия первого ранга
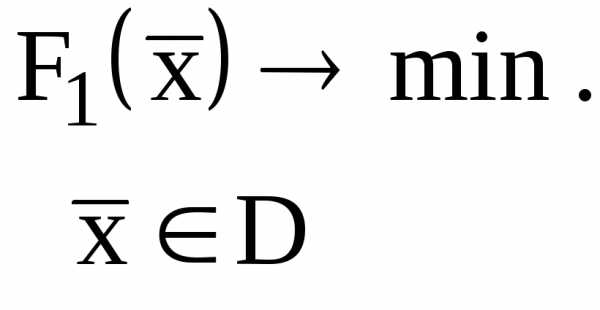 (18)
(18)
Третий подход — формирование обобщённого критерия. Идея этого метода проста: построить обобщённый скалярный критерий
(24)
как функцию исходных критериев. Пусть минимизируются все частные критерии, чего легко добиться, умножив максимизируемые критерии на -1. При этом минимум обобщённого критерия (24) должен соответствовать решению многокритериальной задачи. Тогда решение поставленной задачи сведётся к обычной оптимизации
. (25)


50. Одномерная оптимизация.
4.1. Метод равномерного поиска
Пусть априорная информация об унимодальности функции крайне недостаточна, чтобы строить разумный процесс поиска экстремума. Наиболее приемлемым способом поведения в такой обстановке является последовательное вычисление целевой функции I(y) при всех допустимых значениях варьируемого параметра y
a y b ,
где a, b - границы интервалов поиска.
Пусть заданная величина погрешность определения оптимального параметра y*. Тогда для реализации алгоритма поиска следует определить значение I(y) в
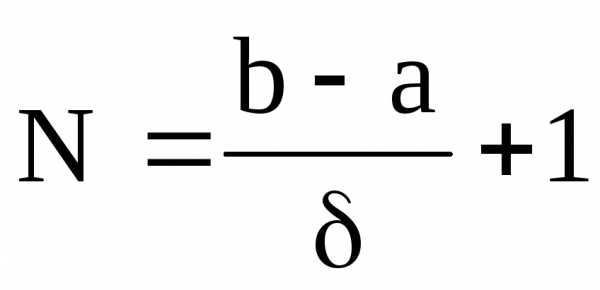
точках, равномерно отстоящих друг от друга на расстоянии h=, т. е. в точках
Из полученных значений показателя качества I(yj) выбирается наибольшее значение (глобальный максимум). Такой способ поиска называется сканированием. При малой заданной погрешности этот метод требует слишком большое число вычислений функции I(y) и больших затрат машинного времени.
4.2. Метод поразрядного приближения
Этот метод применим для поиска оптимума унимодальной функции и обладает более высоким быстродействием. Это достигается тем, что используется алгоритм с переменным шагом поиска. Вначале величина шага выбирается достаточно большой, значительно превышающей требуемую погрешность определения положения оптимума, и выполняется грубый поиск. В районе оптимума поиск производится с меньшим шагом.
Задается начальное значение параметра y0 = a и вычисляется I0=I(y0). Задаются начальный шаг поиска h и кратность k уменьшения шага в районе оптимума. Производится поиск максимума I(y) из начальной точки y = y0 по алгоритму
y(j+1)=y(j)+h(j+1);
(25)
где j - номер шага.
По этому алгоритму поиск из начальной точки y = y0 осуществляется с постоянным шагом h. После каждого шага вычисляется значение критерия I(y), оно сравнивается с предыдущим значением и в случае улучшения критерия шаги продолжаются до тех пор, пока очередной шаг не окажется неудачным. После этого поиск максимума продолжается из последней точки в обратном направлении с шагом в k раз меньше прежнего. Эта процедура поиска продолжается до тех пор, пока не будет выполнено условие
h ,
где - заданная погрешность определения оптимума.
4.3. Метод дихотомии
Этот метод отыскания экстремума применим для класса унимодальных функций. Идея метода проста - делить интервал [a, b], где расположен оптимум I(y), пополам
y0 = (a + b)/2
и отбрасывать часть, где оптимума заведомо быть не может. С этой целью достаточно вычислить показатель качества I(y) в точках y0 d, отстоящих друг от друга на расстояние 2d < , где - заданная погрешность определения оптимума. По двум вычисленным значениям I(y0 - d) и I(y0 + d), в силу унимодальности функции I(y), легко установить новый интервал неопределенности по следующим условиям (при поиске максимума):
(26)
Таким образом, в результате двух вычислений I(y) промежуток, где содержится оптимум, сокращается почти вдвое. Следующая пара измерений проводится в районе середины нового интервала неопределенности [a, y0 + d] или [y0 - d, b] в зависимости от того, какое из условий (26) выполняется.
Аналогично производятся последующие шаги поиска до тех пор, пока на k-ом шаге после 2k измерений I(y) длина интервала неопределенности lk = (b-a)/2k, где находится оптимум, не станет меньше или равен , т. е. lk.
4.4. Метод золотого сечения
В геометрии золотым сечением называется такое деление отрезка на две неравные части, при котором отношение всего отрезка к большей части равнялось отношению большей части к меньшей.
studfiles.net
Классификация задач оптимизации экономических систем — МегаЛекции
Концепция оптимального управления логически приводит к понятию оптимума. Этому понятию соответствует комплекс представлений о таком состоянии экономики (или о таком режиме функционирования), которое является в определенном смысле наилучшим среди всех возможных и в наибольшей степени обеспечивает реализацию целей социально-экономической системы. Исходными предпосылками для формирования этих представлений являются следующие очевидные факты: плановая экономика должна функционировать сбалансировано; потери ресурсов недопустимы, и они должны использоваться наиболее эффективным образом; производство должно удовлетворять конечные потребности общества и др. Развитие экономической теории позволило получить более сильные формулировки этих основополагающих положений, связав их с принципами оптимального управления.
Соответствие экономической деятельности целям общественного развития должно быть подкреплено эффективным хозяйственным механизмом. Это означает, что понятие оптимума связано с построением механизма, обеспечивающего его реализацию.
В процессе функционирования экономики должен быть реализован оптимальный план, обеспечивающий максимизацию общественного благосостояния при выполнении ограничений всех видов. Вытекающие из оптимального плана управляющие воздействия определяют условия хозяйственной деятельности в системе, в рамках которых реализуются экономические интересы коллективов и отдельных работников. Экономические интересы выражают наиболее эффективные для хозяйственных субъектов варианты производственной деятельности в границах, задаваемых планом и стимулирующими воздействиями, включающими поощрения за выполнение плановых заданий и санкции за их невыполнение. Таким образом, экономические интересы могут способствовать или препятствовать выполнению оптимального плана.
В условиях определенной хозяйственной самостоятельности хозяйственных ячеек оптимальный план может быть выполнен только при согласованной системе экономических интересов, включая общественный интерес.
Согласование интересов должно обеспечиваться как за счет выбора оптимального плана, определения необходимых стимулирующих воздействий, так и за счет создания условий для такого согласования непосредственно на нижних уровнях. Трудности согласования при вертикальных воздействиях в рамках оптимального плана связаны, прежде всего, с тем, что на верхних уровнях в процессе разработки плана невозможно полностью учесть возможности локальных хозяйственных звеньев, внутренние мотивы деятельности производственных коллективов и отдельных работников и другие социальные факторы и ограничения.
Формализация в этой области наталкивается на значительные трудности, что связано как с недостаточностью теоретических и прикладных исследований процессов коллективного поведения (в том числе в сфере экономики), так и с относительно слабой формализуемостью самих изучаемых явлений и процессов, носящих стохастический характер и не поддающихся точному предвидению. Поэтому «лобовое» использование здесь нормативного подхода к моделированию с декретированием желательных результатов этих процессов без достаточных предварительных знаний об объекте, обладающем способностью к самоорганизации, не может оказаться плодотворным. Такие знания могут быть получены только посредством дескриптивных поведенческих моделей, позволяющих выявить основные зависимости реакции объекта на изменение внешних условий.
Тем самым с позиций системного подхода уже на уровне отдельно взятой хозяйственной ячейки обнаруживается необходимость синтеза нормативных и дескриптивных методов исследования и, соответственно, моделей. Основной функцией первых в данном случае является директивное определение плановых показателей деятельности ячеек с учетом условий ее осуществления и интересов хозяйственных субъектов. Задача вторых – прогностическое описание возможного поведения ячеек в рамках, определяемых их хозяйственной самостоятельностью и выбором решений в соответствии с собственными интересами. Только таким путем может быть достигнуто наиболее адекватное (с точностью до границ формализуемости, степени предсказуемости и возможностей имеющегося аппарата моделирования) отражение реальных процессов функционирования отдельных звеньев экономики, получена новая информация об их производственном «потенциале» в плановом периоде. Учет последней при разработке плана позволяет обществу выявить дополнительные резервы повышения эффективности общественного производства. А именно в этом и заключается одна из главных причин, определяющих целесообразность перехода к системному моделированию экономики.
Выход за рамки обычного рассмотрения отдельной хозяйственной ячейки связан с ее представлением как элемента экономической системы, обладающего разветвленными внешними взаимосвязями и взаимодействующего в процессе своего функционирования с другими элементами. Иерархическая организационная структура хозяйствования вносит в множество взаимосвязей системы вертикальное и горизонтальное упорядочение, обеспечивая на практике условия для централизованной координации деятельности различных подсистем, направленной на достижение целей развития общества. На этапе планирования она заключается в выработке и согласовании принимаемых решений на разных уровнях иерархии (вертикальная взаимоувязка плановых расчетов) и между отдельными ячейками одного уровня (горизонтальная взаимоувязка расчетов). Необходимость такой взаимоувязки объясняется рядом причин. Изолированно получаемые планы локальных ячеек при ограниченной информации о положении системы в целом могут оказаться несовместимыми при их объединении из-за нарушения ограничивающих условий для системы в целом. Эта ситуация приводит к тому, что, даже если множество локальных решений образует допустимый план, весьма маловероятно, что он будет оптимальным с точки зрения экономики в целом.
Взаимообусловленность развития хозяйственных ячеек, требующая для принятия решений в одной из них информации о намечаемой в плановом периоде деятельности других, технические требования к организации эффективного управления сложной экономической системой (одним из которых является обратимое «сжатие» информации по мере перехода от низших уровней иерархии к высшим) и, наконец, необходимость последовательного выявления интересов локальных хозрасчетных ячеек и их взаимоувязки с общественными интересами на практике привели к итерационному планированию процессов экономического развития. В ходе данного процесса происходит поэтапное уточнение исходных представлений об объекте управления, позволяющее добиваться более тесной сбалансированности плана в смысле производственно-технологической и институциональной структуры. С этой точки зрения переход к системе моделей, механизм согласования решений в которой отражает важнейшие черты реального процесса разработки плана[2], имеет большое практическое значение.
Формальный аспект проблемы согласования планово-хозяйственных решений в системе моделей оптимального планирования заключается в том, чтобы путем изменения «входных» и «выходных» параметров взаимосвязанных моделей получить локально-оптимальные решения, дающие глобальный оптимальный план. Естественно, что говорить о его соответствии реальному оптимуму экономической системы можно лишь с точностью до принятых при построении моделей и механизма их взаимодействия предпосылок. Поэтому основным здесь является содержательный аспект проблемы: по каким параметрам, характеризующим моделируемые объекты, происходит взаимоувязка; насколько полученное решение определяет реальную согласованность их деятельности.
Если бы структурная организация экономической системы сводилась к производственно-технологической структуре хозяйства, то задача планирования заключалась бы в выборе на множестве допустимых возможностей ячеек вариантов производства, отвечающих глобальному критерию оптимальности, и их согласовании между собой. Для этого достаточно было бы на уровне экономики в целом разработать межотраслевые (натурально-вещественные и финансово-стоимостные) балансы производства и распределения различных благ, услуг и ресурсов с построением на их основе системы балансово-оптимизационных моделей, охватывающей основные уровни организационной иерархии.
Институциональная структура предъявляет свои требования как к найденному решению, так и к самой процедуре согласования, в ходе которой должна происходить взаимоувязка интересов хозяйственных ячеек с интересами системы в целом так, чтобы получаемый в результате расчетов производственно-технологический план был эффективным и с общеэкономических позиций, и с позиций отдельных локальных звеньев экономики.
Можно выделить два основных подхода к решению этой задачи. Первый подход основан на предположении, что подобное согласование может быть достигнуто путем редукции (декомпозиции) экзогенно заданного глобального критерия на множество локальных критериев оптимальности при соответствующем выборе основных регулирующих параметров функционирования (цен, рентных платежей и т. д.). Второй подход исходит из принципа композиционного представления глобального критерия (хотя и в неявном виде) как комбинации критериев оптимальности хозяйственных ячеек, включая центр, представляющий интересы экономической системы, и его последующего уточнения в процессе расчетов.
Сообразно с этим все многообразие предложенных в литературе многошаговых итерационных процедур согласования решений в системе моделей оптимального планирования можно разделить на два больших класса: процедуры декомпозиционного типа, среди которых выделяются алгоритмы блочного линейного и нелинейного программирования [14, 26], аппроксимационные методы [46], методы итеративного агрегирования [20], и процедуры композиционного планирования, основанные на механизмах локально-оптимальных экономических взаимодействий [13].
Сложность производственных взаимосвязей и необходимость обеспечения гибкости всей производственной системы вызывает необходимость определенной хозяйственной самостоятельности локальных звеньев, их участия в разработке плана, то есть в установлении горизонтальных взаимосвязей. Это необходимо для того, чтобы хозяйственные ячейки были заинтересованы в повышении эффективности своей производственной деятельности, в мобилизации внутренних резервов. Вместе с тем хозяйственная самостоятельность в условиях агрегированности плановых заданий, известной свободы в определении некоторых аспектов производственной программы может привести к локальным решениям, которые, даже будучи согласованными между собой, не будут отвечать требованиям оптимального плана и, таким образом, оптимума.
Если социальные факторы, проявляющиеся в реальном функционировании экономики, не обеспечивают при заданном оптимальном плане согласования интересов и, таким образом, оптимальный план, выработанный системой управления, не реализуется, то это означает, что постановка задачи управления была в существенной степени неточной, что действительные возможности экономики и экономического управления были определены неверно.
Механизм деятельности за счет установления горизонтальных хозяйственных взаимосвязей на нижних уровнях не смог компенсировать неточности в определении оптимального плана и оказался нереализуемым. Это означает, что в существующих условиях он не обеспечивает оптимума и должен быть изменен.
Разработка нового оптимального плана предполагает изменение параметров задачи, стоящей перед экономическим управлением, то есть параметров критерия оптимальности и, возможно, уровней целевых ограничений.
Следовательно, решение задачи отыскания плана, обеспечивающего оптимум, может проходить в несколько этапов, в которых взаимно корректируются условия задачи, характеристики хозяйственного механизма и решения локальных звеньев. Полученный в результате вариант плана является оптимальным с учетом корректировки условий задачи, сохраняет все свойства оптимального плана, то есть позволяет определить важнейшие параметры оптимального управления, и вместе с тем является реализуемым и, таким образом, соответствует оптимуму.
Таким образом, понятие «оптимум» характеризует режим функционирования экономики в соответствии с планом, при котором достигается наилучшее с общественной точки зрения использование производственных ресурсов на основе обеспечивающего реализацию этого плана согласования экономических интересов всех хозяйственных звеньев.
Модельная реализация принципа оптимума связана с представлением экономики и ее подразделений в виде экономико-математических моделей, расчеты по которым позволяют отыскать оптимальный план и определить существенные параметры хозяйственного механизма, реализующего его. Оптимум должен удовлетворять двум группам требований: требованиям «извне», то есть требованиям со стороны общественной системы, и требованиям «изнутри», то есть требованиям реализуемости. В соответствии с этим можно выделить два класса моделей в зависимости от того, какие требования положены в основу их построения.
Первый класс моделей составляют модели оптимизационного типа, которые позволяют рассматривать построение плана экономического развития как оптимизационную задачу. Ее математической формулировкой является задача оптимального управления, структура которой определяется двумя группами условий. Это, во-первых, целевая функция (максимизируемая или минимизируемая) и, во-вторых, множество допустимых решений, задаваемое ограничениями в пространстве переменных задачи. В таком случае задача нахождения оптимального плана заключается в поиске экстремума целевой функции и имеет смысл, когда множество допустимых планов непусто и не сводится к одной точке, а целевая функция на этом множестве ограничена (сверху – при максимизации, снизу – при минимизации).
Правомерность такого подхода к построению оптимального плана экономического развития обосновывается следующими соображениями. Возможности экономики по производству средств удовлетворения потребностей общества в каждый момент времени ограничены. Вместе с тем взаимозаменяемость ресурсов и технологий, способов удовлетворения потребностей обеспечивает многовариантность возможностей экономического развития. Таким образом, можно установить соответствие между множеством допустимых планов экономического развития и областью возможных решений задачи. Принцип оптимума требует выбора наилучшего из всех возможных планов, который может быть представлен как отыскание экстремального значения функции, определенной на множестве планов и выражающей их качество. Как мы видим, соответствие может быть установлено и здесь, то есть поиск оптимального плана развития может быть осуществлен (теоретически) посредством решения условно-экстремальной задачи:
Вместе с тем необходимо отметить, что такой подход к решению задачи выбора наилучшего плана экономического развития сохраняет известную условность. До настоящего времени остается не вполне понятным, какой вид должна иметь экстремизируемая функция. Очевидно, что она должна выражать степень соответствия требованиям, предъявляемым к народному хозяйству, и давать возможность сравнивать по этому признаку различные планы. Но какой показатель, какая функция от экономических параметров обладает этим свойством, – этот вопрос до сих пор является дискуссионным.
Единая целевая функция экономики гарантирует целостность подхода и в то же время определяет ограниченность постановки проблемы. Данный подход направлен на обеспечение принципа соответствия социально-экономического развития и в гораздо меньшей степени позволяет выявить характеристики эффективного хозяйственного механизма, без которого оптимум невозможен. И дело здесь не только в нереальности практического решения оптимизационной задачи для экономики в целом. Нельзя, конечно, утверждать, что теоретическая постановка единой оптимизационной задачи бесполезна для построения хозяйственного механизма. Такая задача выражает основную идею оптимизационного подхода и позволяет сформулировать фундаментальные положения, имеющие важное значение в пределах всего подхода, в том числе и при построении реализующего оптимальный план механизма. Таковы, например, выводы об оптимальных оценках и их свойствах в оптимальном плане. Но, тем не менее, структура такой задачи не позволяет содержательно анализировать проблемы создания эффективного хозяйственного механизма, поскольку в ней явно не представлена совокупность локальных хозяйственных звеньев в их сложном взаимодействии.
Дальнейшее развитие идея оптимума получила в оптимизационных моделях многоуровневого типа, реализующих декомпозиционный принцип определения плана экономического развития. При построении таких моделей единая многоразмерная оптимизационная задача заменяется рядом задач, относящихся к различным уровням экономики и имеющих меньшую размерность. Соответствующие модели различаются составом входящих в них блоков.
Обычно модели включают в себя задачи, относящиеся к уровням экономики в целом, отрасли, региона, производственных объединений и предприятий. Построение оптимального плана осуществляется посредством согласованных расчетов по локальным оптимизационным задачам. Согласование процесса обеспечивается итерационным путем.
Такой подход к решению проблемы нахождения оптимального плана экономического развития основан на структуризации единой глобальной задачи. Выделение взаимосвязей между подразделениями экономики представляет собой существенное продвижение в направлении определения характеристик хозяйственного механизма. Тем не менее, многоуровневая модель основана на идее единой и охватывающей все уровни оптимизации. На практике это означает, что локальные критерии оптимальности должны быть построены в соответствии с глобальным критерием. Иначе говоря, целевые функции локальных задач должны быть согласованы с целевой функцией макрозадачи. Локальная оптимизация должна обеспечивать экстремум глобальной функции. В модели ищутся схемы и параметры взаимодействия, обеспечивающие такое согласование. Тем самым определяются и параметры хозяйственного механизма.
Подчиненность локальных оптимизаций глобальной в рамках декомпозиционных схем оптимизации сохраняет идею единой оптимизационной задачи, а значит, и такую ее особенность, как способность учитывать, главным образом, требования к экономике извне от общественной «надсистемы», и, в гораздо меньшей степени, решать проблему построения эффективного механизма реализации оптимума.
Второй класс моделей составляют модели экономического равновесия, реализующие композиционный принцип составления оптимального плана развития экономики. В таких моделях описываются участники экономической системы – объекты разных уровней, имеющие собственные целевые функции и оптимизирующие свое функционирование в системе. Эти функции выражают их цели в социально-экономической системе и не выводятся из целевой функции экономики в целом, как в моделях оптимизационного типа. Состоянием оптимума считается такое состояние, в котором интересы отдельных участников и экономики в целом оказываются согласованными.
Такой подход предполагает повышенное внимание к установлению правил взаимодействия экономических объектов.
Модели экономического равновесия дают возможность заменить проблему построения глобального критерия оптимальности изучением целевых функций экономических объектов и определением правил взаимодействия, приводящих экономику в согласованное, равновесное состояние.
Одним из допустимых способов формализации указанной проблемы является теоретико-игровая постановка задачи, при которой на множестве возможных стратегий задаются «игроки» и их «функции выигрыша». Точкой равновесия является такой набор стратегий участников (или способов функционирования в экономике), когда ни одному из них в отдельности при его функции выигрыша не выгодно менять стратегию. При более общем подходе к определению понятия «равновесие» точками, обеспечивающими равновесие экономической подсистемы, считаются такие состояния экономики, которые не могут быть изменены таким образом, чтобы состояния всех участников не ухудшились (в соответствии с их целевыми функциями), а состояние хотя бы одного из них улучшилось. Такие состояния образуют множество эффективных точек и называются оптимальными по Парето.
Эффективные точки определяют равновесие системы, поскольку в них согласовываются интересы участников, а переход к любой неэффективной точке нарушает равновесие. Так, улучшение значения целевой функции одного участника неизбежно влечет за собой ухудшение положения другого участника. Вместе с тем при таком понимании равновесия переход к другой эффективной точке не нарушает равновесия. Различные состояния равновесия, определяя реализуемые состояния экономики, в разной степени соответствуют целям социально-экономической системы. Поэтому для обеспечения оптимума в модель необходимо вводить дополнительные условия, позволяющие сужать множество эффективных точек. Эти условия представляются в виде правил распределения ресурсов и продуктов в экономической подсистеме. Собственно говоря, нахождение эффективных точек в этом случае основывается на определенном принципе распределения, запрещающем увеличение благосостояния отдельных участников или суммарного благосостояния в системе за счет ухудшения благосостояния других участников. Но достижение оптимума требует использования дополнительных соображений. Оптимальный план заведомо соответствует эффективной точке. Эффективное же состояние является оптимальным при фиксированных принципах распределения, устанавливающих существенные черты механизма функционирования и обеспечивающих выполнение требований со стороны общества.
Описание экономики оптимизационными и равновесными моделями – это два способа ее представления как оптимально функционирующей экономики.
В заключение следует отметить, что эффективность хозяйственного механизма тесно связана с социальными условиями реализации оптимума. Помимо целевых ограничений, социальные факторы, очевидно, воздействуют на экономические процессы, прежде всего, через вовлечение в производство трудовых ресурсов. Однако общий объем трудовых ресурсов, их профессионально-квалификационный состав – это еще не социальные факторы в производстве. Данные характеристики представляют трудовую деятельность как производственный ресурс, который при составлении плана учитывается наравне с другими. Социальная, неэкономическая природа трудовых ресурсов проявляется в том, что работники осуществляют выбор своего поведения в системе, в том числе, выбор интенсивности и места приложения трудовой деятельности. Мотивы выбора не могут быть сведены к экономическим, а значит, и не могут быть достаточно полно отражены в оптимизационных (и равновесных) моделях. Территориальная миграция, выбор профессии – эти процессы могут быть описаны в экономических терминах лишь приближенно, например, через стремление к получению большего дохода. Очевидно, что причины, вызывающие те или иные сдвиги в структуре трудовых ресурсов, гораздо разнообразнее и сложнее. И это может оказаться причиной несоответствия фактического распределения трудовых ресурсов в производстве требованиям, полученным в результате расчетов по оптимизационным моделям.
15.3 Важные частные случаи
Для двух частных классов задач оптимизации имеется хорошо разработанная теория. Кроме того, во многих других случаях используются методы, основанные на принципах одного или обоих частных классов задач. Это – задача линейного программирования и классическая задача на условный оптимум.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
§6. Классификация детерминированных задач оптимизации.
Рассмотрим детерминированную задачу оптимизации
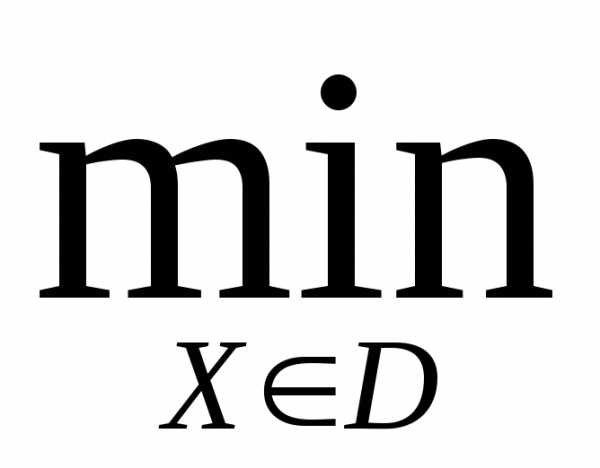 (1)
(1)
где область допустимых значений 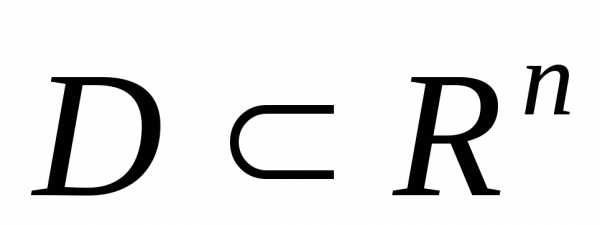 ,
,
(2)
Классификация задачи (1, 2) возможна по многим признакам. Рассмотрим основные из этих признаков.
Классификация по виду критерия оптимальности и ограничивающих функций.
Если критерий оптимальности Ф(Х) – линейная функция, а множество D – выпуклый многогранник, то задача (1), (2) называется задачей линейного программирования.
Если критерий оптимальности Ф(Х) – есть отношение двух линейных функций, а множество D – выпуклый многогранник, задача (1), (2) называется задачей дробно-линейного программирования.
Пусть область D определяется только ограничениями типа неравенств:
(3)
Тогда если функция Ф(Х) и функции являются сепарабельными, то задача (1), (3) называется задачей сепарабельного программирования.
Если функция Ф(Х) и ограничивающие функции являются позиномами, то задача (1), (2) называется задачей геометрического программирования.
Если Ф(Х) – квадратичная функция, т.е. , а множество D есть выпуклое множество, то задача (1), (2) называется задачей квадратичного программирования. Здесь G-(n*n) симметричная матрица, С-(n*1) вектор.
Задачи линейного, дробно-линейного, сепарабельного и геометрического программирования редко возникают в САПР и в данном курсе не рассматриваются.
Если множество D является конечным множеством, то задача (1), (2) называется задачей дискретного программирования.
Если множество D является множеством целых чисел, то задача (1), (2) называется задачей целочисленного программирования.
Задачи дискретного и целочисленного программирования обычно изучаются в курсах исследования операций и в данном курсе не рассматриваются.
Если функция Ф(Х) является выпуклый, то задача (1), (2) называется задачей выпуклого программирования. Заметим, что определение выпуклой функции Ф(Х) требует выпуклости области ее определения D.
В общем случае задача (1), (2) называется задачей нелинейного программирования. Часто задачи выпуклого программирования также относят к задачам нелинейного программирования.
Классификация по наличию или отсутствию ограничений.
Если ограничения на вектор Х отсутствуют (т.е. D=Rn), то задача (1), (2) называется задачей оптимизации без ограничений или задачей безусловной оптимизации.
Если имеются ограничения на вектор Х (т.е. 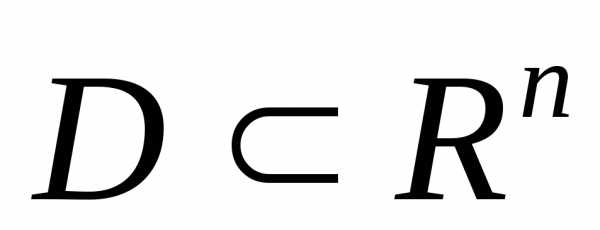 ), то задача (1), (2) называетсязадачей оптимизации с ограничениями или задачей условной оптимизации.
), то задача (1), (2) называетсязадачей оптимизации с ограничениями или задачей условной оптимизации.
Классификация по характеру ограничений.
Среди задач условной оптимизации выделяют следующие классы задач:
;
;
задачи условной оптимизации с ограничениями общего вида, когда имеются как ограничения типа неравенств, так и ограничения типа равенств, т.е. когда
Классификация по размерности вектора Х.
Если размерность вектора Х равна 1 (n=1), то задача (1), (2) называется однопараметрической (одномерной) задачей оптимизации.
Если размерность вектора Х больше 1 (n>1), то задача (1), (2) называется многопараметрической (многомерной) задачей оптимизации.
Классификация по количеству точек минимума.
Если функция Ф(Х) имеет в области допустимых значений D один минимум, то задача (1), (2) называется одноэкстремальной задачей оптимизации.
Если функция Ф(Х) имеет в области допустимых значений D более одного минимума, то задача (1), (2) называется многоэкстремальной задачей оптимизации.
Классификация по характеру искомого решения.
Если отыскивается любой локальный минимум функции Ф(Х), то задача (1), (2) называется задачей локальной оптимизации.
Если отыскивается глобальный минимум функции Ф(Х), то задача (1), (2) называется задачей глобальной оптимизации.
26
studfiles.net
Классификация задач оптимизации - Справочник химика 21
Классификация задач оптимизации надежности. . . . [c.5]КЛАССИФИКАЦИЯ ЗАДАЧ ОПТИМИЗАЦИИ НАДЕЖНОСТИ [c.200]
По функционально-структурному признаку задачи оптимизации надежности объектов разделим на два вида задачи оптимизации показателей надежности ХТС и показателей надежности отдельных единиц оборудования. Вначале рассмотрим классификацию задач оптимизации показателен надежности ХТС. В зависимости от применяемых общих методов повышения надежности, а также организационно-технических и технологических способов повышения надежности ХТС, подробная характеристика которых приведена в гл. 3 и 4, выделяют следующие инженерно-технические типы задач оптимизации надежности ХТС задачи оптимального резервирования (задачи оптимального управления запасами элементов) с одним или несколькими ограничениями задачи оптимальной технической диагностики задачи оптимального технического обслуживания. [c.200]
Классификация задач оптимизации [c.379]В табл. 1 дана характеристика областей применения различных методов оптимизации, при этом за основу положена сравнительная оценка эффективности использования каждого метода для решения различных типов оптимальных задач. Классификация задач проведена по следующим признакам 1) вид математического описания процесса 2) тип ограничений на переменные процесса и 3) число переменных. Предполагается, что решение оптимальной задачи для процессов, описываемых системами конечных уравнений, определяется как конечный набор значений управляющих воздействий (статическая оптимизация процессов с сосредоточенными параметрами), а для процессов, описываемых системами обыкновенных дифференциальных уравнений, управляющие воздействия характеризуются функциями времени (динамическая оптимизация процессов с сосредоточенными параметрами) или пространственных переменных (статическая оптимизация процессов с распределенными параметрами). [c.34]
Прежде чем перейти к решению второй задачи оптимизации, рассмотрим кратко классификацию дискретных оптимизируемых параметров. Всю совокупность параметров можно разделить на четыре группы. [c.363]
В соответствии с. принятой выше классификацией независимых переменных при решении основной задачи оптимизации варьируются только конструктивные переменные, определяющие компоновку аппарата при фиксированных значениях технологических параметров. Следовательно, в рамках основной задачи расходы теплоносителей остаются постоянными. [c.303]
Более подробный анализ задач и методов оптимизации дан в гл. V. Многообразие задач оптимизации привело к большому числу разнообразных методов и алгоритмов для их решения. На рис. 1.33 приведена классификация этих методов. Наиболее эффективные методы описаны в гл. V. Существенное значение при оптимизации имеет постановка задачи, т. е. требуется ли нахождение лишь оптимальной точки, или всего компромиссного множества точек или всей структуры оптимального решения в зависимости от некоторых параметров, как например, при оптимизации структуры ХТС. [c.38]
Дадим здесь классификацию и краткую характеристику применяемых методов оптимизации с. х.-т. с. Рассмотрим вначале наиболее часто встречающуюся задачу оптимизации статических [c.11]
Основные обозначения и классификация задач принятия решений при оптимизации функционирования ХТС [c.239]
Первая глава посвящена математической постановке задачи проектирования поверхностных теплообменников-конденсаторов как задачи оптимизации при наличии ограничений. В ней приводится классификация теплообменников-конденсаторов химико-технологических процессов, формируются векторы оптимизируемых параметров при проектировании различных типов аппаратов, обсуждается возможность использования для целей проектирования различных технико-экономических критериев. В заключение рассматривается алгоритм функционирования системы оптимального проектирования теплообменников-конден-саторов и возможные пути его реализации. [c.5]
Классификация, иерархия и взаимосвязь задач оптимизации ГПЗ. [c.330]
ВЕКТОРНЫЙ подход И КЛАССИФИКАЦИЯ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ ХТС [c.17]
Существуют разнообразные способы классификации сбросных сооружений [Чугаев, 1975]. Для задачи выбора параметров гидроузлов по условиям пропуска паводков центральным вопросом является характер связи между сбросными расходами и уровнями воды в верхних и нижних бьефах водохранилищ. Поэтому, прежде всего, разделим все сбросные сооружения на две группы напорные и безнапорные. Сооружения первой группы условно будем называть водовыпусками, а второй — водосливами. Для повышения инвариантности математической модели по отношению к различным местным условиям регулирования стока паводков целесообразно создать регулярно пополняемую базу данных В, содержащую различные конструктивные, технические и стоимостные характеристики сбросных сооружений. Первоначально в эту базу включаются наиболее широко применяемые конструкции, например, некоторые из числа представленных в справочнике [Киселев, 1972], а затем она постепенно пополняется новыми типами сооружений. При этом до решения задачи оптимизации допустимое множество В конструкций сбросных сооружений каждого j-ro гидроузла задается согласно локальным особенностям в j-м створе. Тогда на выбор конкретного конструктивного типа j сбросного сооружения в каждом створе накладываются дискретные ограничения вида [c.410]
Исходя из идей системного анализа каждый типовой процесс необходимо рассматривать как самостоятельную сложную систему, но вместе с тем являющуюся лишь отдельной подсистемой еще более сложной системы — предприятия, отрасли. Соответственно этому должны различаться и задачи технико-экономической оптимизации. Это хорошо видно из классификации задач техникоэкономической оптимизации ХТС, обсуждаемых в следующем параграфе. [c.20]
Для решения задачи оптимизации ведения разведочных работ необходимо выполнение статистического анализа всех работ, связанных с разведкой большого числа месторождений. На основе этого анализа можно составить классификацию месторождений и вывести зависимости минимального и максимального числа разведочных скважин от типа место- [c.211]
Задача синтеза систем оптимизации оборудования решается на двух уровнях структурном и модульном (рис. 89) При использовании новых, функциональных классификаций оборудования и основных видов его расчета анализируется все множество расчетных задач. На основе анализа выделяются общие н специфические элементы расчетов с распределением на иерархические уровни при учете степени общности и их взаимосвязи. [c.320]
В третьей главе рассмотрен автоматизированный структурно-параметрический синтез гибких химико-технологических систем. Изложены задачи синтеза систем в условиях полной и неполной определенности информации. Отдельный параграф посвящен математическим методам и вычислительным алгоритмам структурно-параметрического синтеза систем дискретного типа. Изложены методы автоматической классификации технологических процессов, оптимизации технологической структуры и аппаратурного оформления химико-технологических систем периодического действия — алгоритмы эвристического типа, ветвей и границ , случайного поиска, геометрического программирования, комбинированные. [c.6]
Как установлено выше, создание гибких автоматизированных химических производств немыслимо без рассмотрения проблемы оптимизации структуры ХТС, решение которой сводится к решению той или иной модификации задач группировки ( классификации) конечного множества объектов (видов сырья, продукции, типов оборудования, тары, совокупности технологических операций, процессов...) в заданном пространстве признаков на конечное число групп (классов), состоящих из сравнительно однородных в некотором смысле элементов. [c.256]
В рамках такой классификации наиболее перспективным представляется первый подход к решению задачи расчета процесса многокомпонентной ректификации в силу его общности. Основным недостатком такого подхода является необходимость использования для решения задачи ЭВМ с очень большим быстродействием и объемом оперативных запоминающих устройств [130, 247, 244]. Для второй группы методов характерно то обстоятельство, что размерность решаемой системы уравнений удается снизить лишь в случае использования различного рода упрощений (идеальность разделяемой смеси, теоретическая ступень разделения). Если же учитывать, например, неидеальность разделяемой смеси, то размерность задачи возрастает до первоначальной [229, 247]. Методы третьей группы рекомендуется использовать лишь при проведении большого числа однообразных расчетов (например, при использовании их с некоторыми алгоритмами оптимизации). Главные же их недостатки заключаются в том, что для задач даже одного и того же класса слишком велика вероятность получения расходящегося итерационного процесса, например в случае зависимости скорости сходимости от величин режимных параметров [215]. Аналогичные недостатки присущи и ряду других используемых в настоящее время алгоритмов. [c.51]
Согласно приведенной классификации, разница в характере частных задач технико-экономической оптимизации ХТС обусловлена различием в уровне решения оптимизационных задач и во времени. [c.25]В соответствии с классификацией частных задач технико-экономической оптимизации на каждом уровне решения оптимизационные задачи дифференцируются на задачи технико-экономической оптимизации проектируемых ХТС и задачи технико-экономической оптимизации действующих ХТС. Дифференциация обусловлена спецификой требований, предъявляемых к этим задачам. [c.26]
Описанная классификация частных задач технико-экономиче-ской оптимизации ХТС открывает возможности для создания наиболее эффективного инструмента оптимизации — комплекса специализированных экономико-математических моделей, каждая из которых может использоваться для оптимизации различных по степени сложности элементов ХТС применительно к целям и особенностям определенного уровня, этапа и стадии техникоэкономической оптимизации. [c.27]
В производствах ООС и СК применяются самые разнообразные реакторы поэтому необходимо их четко классифицировать. В последние годы в научной литературе предложено много вариантов классификации реакционной аппаратуры. Во многих случаях эти предложения связаны с конкретными задачами, например, моделирования и оптимизации химических производств . [c.69]
Проведенный в этом параграфе анализ методов оценки качества процессов разделения показал их несоответствие совокупности граничных условий, отражающих задачи, решаемые классификацией, что не позволяет в полной мере рекомендовать эти соотношения для оптимизации процессов классификации. [c.37]
Существует необозримое л трудно поддающееся классификации множество вариантов задач оптимизации, связанных как с конкретизацией функционала J и мнозкеств Ки и Ки, так и с обобщением приведенной постановки путем, например, замены одного критерия качества множеством критериев, введением многоуровневой оптимизации и т. д. каждый из этих вариантов требует, как правило, особых приемов исследования свойств оптимального решения, а также применения подходящих в данной ситуации алгоритмов построения решения. [c.268]
В качестве примера задач упорядочения класса А прп ОФХТС можно привести различные задачи выбора окончательных решений при синтезе, оптимизации ХТС в пространстве многих смешанных (количественных и качественных) и нечетко заданных КЭ. К задачам класса Б монзадачи классификации видов сырья и продукции с целью формирования нод1енклатуры ХТС, работающих в условиях постоянного обновления ассортимента продукции и комплексного использования сырья б) задачи декомпозиции расширенных номенклатур сырья и продукции ХТС на подгруппы с целью формирования из последних базовых номенклатур подсистем ХТС (технологических схем п установок) в) задачи классификации единиц оборудования в пространстве конструкционно-технологических признаков подобия прп формировании гибких и совмещенных схем для комплексного использования имеющегося оборудования г) задачи группировки многостадийных технологических процессов при формировании совмещенных схем и оптимальных маршрутов выпуска продукции д) другие задачи оптимизации структур гибких ХТС. [c.248]
Классификацию сталей по сопротивлению сероводородному растрескиванию осуществляли на основе методик оп- тимизации экспериментальных исследований [7, 119]. Одним. из перспективных способов решения задач оптимизации является использование в качестве критерия оптимизации функции желательности Харрингтона [220]. Для ее построения [c.325]
Классификация методов. Для решений сформулированной в гл. 1 задачи комплексной оптимизации параметров и профиля адсорбционных установок или отдельных ее частей и элементов при однозначно (детерминированно) заданных значениях влияющих факторов могут быть применены многие из известных математических методов поиска экстремума функции многих переменных [49, 50]. Однако при практической их реализации на ЭВМ возникают серьезные вычислительные трудности. Некоторые простейшие, широко известные методы минимизации обычно совершенно непригодны для решения реальных задач. Поэтому проблема выбора наиболее целесообразного метода решения задачи поиска минимума сложной функции из числа существующих имеет большое значение. [c.121]
Ознакомление с литературой [86], в которой с той или иной степенью детализации описываются различные по степени сложности алгоритмы решения векторных задач, позволило осуществить их классификацию, представленную в табл. 1. Согласно последней, общую задачу векторной оптимизации (2.1) можно решать с помощью алгоригмов, которые условно разбиты на две группы. В первую вошли те алгоритмы векторной оптимизации, в которых искомое оптимальное компромиссное решение согласовано с целями и предпочтениями лица, принимающего [c.20]
Классификация алгоритмов решения задач векториой оптимизации [c.20]
Судя по появившимся в последнее время публикациям дезактивация катализаторов привлекает повышенное внимание исследователей. В связи с этим имеется возможность более глубоко понять процессы, лежащие в ее основе. Одной из задач предлагаемой монографии является обобщение имеющихся в этой области данных. Основное внимание в ней обращено на парофазные реакции в присутствии твердых катализаторов, хотя в качестве примеров рассмотрены и некоторые трехфазные реакции. Для таких систем пока не предложена более удобная классификация механизмов потери каталитической активности, чем их деление на вызываемые спеканием, отравлением примесями И блокировкой. Эта классификация будет также использована в монографии. Там, где это возможно, изложение ведется на яшке, близком и понятном химикам-технологам. Для описания тех или иных процессов широко используются подходы, основанные на анализе математических моделей. С точки зрения автора—это наилучший способ рассмотрения сложных явлений, имеющих место в реакциях, сопровождающихся дезактивацией как отдельных гранул, так и всего реактора в целом. Исходя из этого выбрана следующая структура монографии. После общего обзора процессов, приводящих к дезактивации катализаторов, эти процессы рассмотрены раздельно применительно к отдельным гранулам или таблеткам катализатора. Далее анализируется поведение всего реактора. Особое внимание уделено оптимизации режимов его эксплуатации. В заключение рассмотрены основные особенности процессов регенерации катализаторов. [c.10]
Алгоритм многокритериальной оптимизации. Одной из наибо-.лее сложных проблем разработки экономико-математических моделей ХТС является обобщение разнокачественных целей функционирования ее отдельных элементов. Очевидно, что ЭММ наиболее общих систем, отнесенные при их классификации к системам третьего класса, будут моделями векторной оптимизации х Х, Р х)—)-тах, определяющими некоторое множество разумных вариантов с точки зрения нескольких критериев. В настоящее время отечественная и зарубежная литература насчитывает большое число работ, в которых описаны различные алгоритмы решения многокритериальных оптимизационных задач. [c.48]
Критерии качества для оценки разделительных процессов начали разрабатывать в начале XX в. 154]. Однако в основу этих разработок наряду с правильными были положены некоторые ошибочные идеи, которые препятствовали решению поставленной задачи. Со времени появления работ Ханкока, в которых впервые был сформулирован обобщенный критерий качества, прошло более полувека. За это время было предложено, около ста различных зависимостей для выражения эффективности классификации. Множественность критериальных методов, отсутствие единства в вопросе выбора способа оценки и оптимизации разделения создают ситуацию неопределенности при выборе классифицирующих аппаратов и оценке качества их работы. Поэтому в большинстве случаев проектирование новых производств и оптимизация действующего оборудования производятся не на строгой [c.3]
В первом разделе изложена общая стратегия исследования МАХП методами системного анализа и развитый на его основе модульный принцип построения математических моделей систем химической технологии. Второй раздел посвящен проблеме формирования оптимальной технологической структуры МАХП, кратко изложен вопрос об оптимизации ассортимента продукции, сформулированы задачи оптимальной автоматической классификации технологических процессов и стандартной аппаратуры. В третьем разделе описаны математические модели [c.4]
chem21.info
3.1.2. Классификация задач оптимизации.
Важным этапом изучения явлений, предметов, процессов является их систематизация, которая обычно завершается классификацией по ряду признаков, а поскольку признаков может быть достаточно много, то и выполненные классификации могут различаться между собой. Любая классификация должна преследовать достижение поставленных целей. Выбор цели определяет набор тех признаков, по которым она будет проводиться.
Рассмотрим классификацию задач оптимизации по виду математических моделей, которые включают следующие элементы:
исходные данные;
искомые переменные;
зависимости между переменными.
Исходными даннымидля математической модели являются: целевая функцияF(Xj), левые части ограниченийgi(Xj) и их правые частиbi. Исходные данные могут бытьдетерминированнымиислучайными.Детерминированными называются такие исходные данные, когда при составлении модели их точные значения известны.
Искомые переменныемогут бытьнепрерывнымиидискретными. Непрерывными называются такие величины, которые в заданных граничных условиях могут принимать любые значения. Дискретными называются такие переменные, которые могут принимать только заданные значения.Целочисленныминазываются такие дискретные переменные, которые могут принимать только целые значения.
Зависимости между переменными(как целевые функции, так и ограничения) могут бытьлинейнымиинелинейными.Напомним, что линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания. Если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной.
Сочетание различных элементов модели образует различные классы задач оптимизации, которые требуют разных методов решения. Основные классы задач оптимизации приведены в таблице 3.1.
Следует сразу уточнить, что в данном пособии мы рассмотрим решение подобных задач лишь на примере тех, которые относятся к классу линейного программирования. Решение задач такого рода зачастую необходимо при принятии оптимального решения в экономике.
Табл.3.1. Основные классы задач оптимизации.
| Классы задач | Характеристики элементов модели | ||
| Исходные данные | Искомые переменные | Зависимости | |
| Линейного программирования | Детерминированные | Непрерывные | Линейные |
| Целочисленного программирования | Детерминированные | Целочисленные | Линейные |
| Нелинейного программирования | Детерминированные | Непрерывные, целочисленные | Нелинейные |
| Стохастического программирования | Случайные | Непрерывные | Линейные |
3.2. Математическая формализация задачи.
При построении математической модели решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи.
Оптимальное решение — это наилучшее. Но решения, наилучшего во всех смыслах, быть не может. Оно может быть наилучшим, т. е. оптимальным, только в одном, строго установленном смысле. И принимающий решение должен точно представлять, в чем заключается оптимальность решения, т. е. по какому критерию принимаемое решение должно быть наилучшим.
studfiles.net