4. Задача об использовании мощностей (задача о загрузке оборудования). Задача оптимизации использования времени работы станка
Задача оптимизации использования фонда рабочего времени
В общем виде задачу оптимального использования фонда рабочего времени можно сформулировать следующим образом.
Имеется m предприятий (например, филиалов фирмы или предприятий отрасли), которые могут производить n видов продукции. Известны:
1) ai– фонд рабочего времени (например, в человеко-сменах) каждого i-го предприятия ;
2) bj– общая величина потребности (сумма заказов) в продукции j-го вида
3) aij– мощность, или количество продукции j-го вида, вырабатываемой в единицу рабочего времени ( в смену) на i-м предприятии;
4) cij– себестоимость производства единицы j-й продукциии на i-м предприятии.
Требуется составить такой план распределения заказов на выпуск продукции всех видов по всем предприятиям, при котором при полном использовании фонда рабочего времени предприятий суммарные затраты на изготовление продукции в заданной номенклатуре будут наименьшими.
Пусть xij– планируемый объем j-й продукции на i-м предприятии; совокупность этих величин обозначим `X. Тогда целевая функция рассматриваемой задачи имеет вид:
Функциональные и прямые ограничения выглядят следующим образом:
xij≥ 0
Если снять условие полного использования фонда рабочего времени предприятий, то ограничения примут вид неравенства:
а если условие строгого выполнения плана в заданной номенклатуре заменить требованием «не менее», то
Очевидно, что задачу можно решить как задачу линейного программирования симплексным методом. Однако если привести посредством определенных приемов коэффициенты aijк единице (это возможно при условии пропорциональности трудоемкости производства единицы продукции различных видов по всем предприятиям), то данная модель не будет отличаться от модели транспортной задачи и ее можно решить, например, методом потенциалов.
Задача оптимизации численности персонала особенно актуальна для предприятий со значительными колебаниями (например, сезонными) объемов производства, что приводит к существенным изменениям в потребности в рабочей силе.
Задача ставиться следующим образом. Известны объемы производства в каждый из n месяцев (например,n=12) и, следовательно, известно требуемое конкретное число работников в каждый месяц; обозначим требуемое (идеальное) число работников в j-м месяце mj Пусть xj– оптимальное число работников в j-й месяц. Величины xjравнялись бы величинам mj, если бы не существовало затрат по найму или увольнению работников при переходе от (j-1)-го месяца к j-му, которое выражается некоторой функцией ¦j (xj- xj-1). Очевидно, что эта функция определяет затраты по найму работников при xj>xj-1и затраты на их увольнение при xj<xj-1. Отклонение числа работников xjот идеального числа mjтакже приводит к затратам, которые выразим в виде функции gj(xj-mj). Если xj>mj, то это затраты на содержание неработающих работников, а если xj<mj– затраты на сверхурочные работы. Виды функций ¦jи gj могут быть установлены на каждом конкретном предприятии.
Экономико-математическая модель рассматриваемой задачи может быть записана следующим образом:
;
Последнее означает, что xj– это целые неотрицательные числа. Таким образом, данная задача может служить примером задачи целочисленного программирования.
Задания к контрольной работе по теме «Задача о назначениях».
Вариант №1. Назначить четыре вида работ пяти машинам, чтобы минимизировать стоимость
| Виды работ | |||||
| Машины | |||||
Вариант №2. Назначить четыре из пяти должностей пятерым работникам таким образом, чтобы максимизировать прибыль
| Должности | ||||||
| Кандидаты | ||||||
Вариант №3. Назначить четыре вида работы пяти машинам, чтобы максимизировать прибыль
| Виды работ | |||||
| Машины | |||||
Вариант №4. Назначить четыре из пяти должностей пятерым работникам таким образом, чтобы минимизировать стоимость
| Должности | ||||||
| Кандидаты | ||||||
Вариант №5. Корпорации RMC требуется назначить пять должностей пятерым работникам, причем должность 1 должна быть назначена второму работнику. Найдите оптимальное решение на основе матрицы стоимостей, приведенной ниже
| Должности | ||||||
| Кандидаты | ||||||
Вариант №6. Назначить пятерых рабочих на пять рабочих мест на основе матрицы стоимостей, приведенной ниже так, чтобы рабочий 2 был назначен на рабочее место 4 или 5
| Рабочие | ||||||
Вариант №7. Корпорация BKW-фирма, состоящая из нескольких подразделений, которая предлагает работу. Прибыль от выполнения пяти видов работ каждым из шести подразделений, показана ниже. Найдите оптимальное решение. Какое подразделение получит работу? Почему?
| Виды работ | ||||||
| Отделы | ||||||
Вариант №8. Назначить четыре из пяти должностей пятерым работникам таким образом, чтобы максимизировать прибыль, причем должность 4 должна быть обязательно назначена
| Должности | ||||||
| Работники | ||||||
Вариант №9. К матрице прибыли, приведенной ниже, добавить дополнительного работника, который может выполнять виды работ 1, 3 и 5 с прибылью 50, 20 и 100 соответственно. Этот работник, однако, не способен выполнять виды работ 2 и 4. Найти оптимальное решение
| Виды работ | ||||||
| Работники | ||||||
Вариант №10. Найти минимальное и максимальное решение для задачи назначений, приведенной ниже
| Виды работ | ||||||
| Работники | A | |||||
| B | ||||||
| C | ||||||
| D | ||||||
| E |
Вариант №11. 6 претендентов на 5 должностей проходят собеседование. "Оценка"каждого претендента и его ежемесячная зарплата при выполнении различных видов работ показаны ниже в двух отдельных матрицах. Определите назначение на работу на основе "оценки" и отдельно на основе зарплаты. Какова разница в стоимости наилучшего назначения, если вместо минимизации зарплаты максимизировать "оценку?" Содержимое ячеек матрицы не обязательно выражается в долларах или каких-либо денежных единицах.
"Оценка" претендента за месяц
| Должности | ||||||
| Претенденты | ||||||
Ежемесячная зарплата претендента
| Должности | ||||||
| Претенденты | ||||||
Вариант №12. В цехе шесть рабочих были специально подготовлены для обслуживания определенных станков. Эти рабочие могут работать на любом из пяти станков. Цех имеет много заказов и все пять станков постоянно заняты. Один из рабочих, не занятых обслуживанием станка, обычно выполняет канцелярскую работу. На основе приведенного ниже плана стоимости обслуживания каждого станка каждым из пяти рабочих определить оптимальные назначения.
| Станки | ||||||
| Рабочие | A | |||||
| B | ||||||
| C | ||||||
| D | ||||||
| E | ||||||
| F |
Вариант №13. Некий продавец собирается продать 4 автомобиля. Основываясь на ценах, предложенных четырьмя потенциальными покупателями, определить, какую машину должен получить каждый из них, чтобы максимизировать прибыль продавца.
| Chevy | Ford | Dodge | Pontiac | |
| Carol | 5,000 | 4,000 | 3,200 | 4,900 |
| John | 3,500 | 3,500 | 3,100 | 5,000 |
| Harry | 4,200 | 3,700 | 2,950 | 4,750 |
| Paul | 3,800 | 4,100 | 3,000 | 4,600 |
Вариант №14. Некий продавец собирается продать 4 автомобиля. Потенциальными покупателями являетесь Вы и Ваши партнеры. Предложенные Вами и Вашими партнерами цены приведены ниже. Решите эту задачу так, чтобы минимизировать Ваши расходы и расходы Ваших партнеров.
| Chevy | Ford | Dodge | Pontiac | |
| Carol | 5,000 | 4,000 | 3,200 | 4,900 |
| John | 3,500 | 3,500 | 3,100 | 5,000 |
| Harry | 4,200 | 3,700 | 2,950 | 4,750 |
| Paul | 3,800 | 4,100 | 3,000 | 4,600 |
Распределить работы таким образом, чтобы минимизировать временные затраты на выполнение всех работ при условии, что каждый из претендентов получит одну и только одну из работ. Матрица временных затрат каждого претендента на выполнение каждой из работ приведена ниже.
Вариант № 15.
| Работники | Номера работ | |||||
| Иванов | ||||||
| Петров | ||||||
| Сидоров | ||||||
| Копылов | ||||||
| Минин | ||||||
| Резько |
Вариант № 16.
| Работники | Номера работ | |||||
| Качурова | ||||||
| Панова | ||||||
| Стевко | ||||||
| Санин | ||||||
| Пинских | ||||||
| Петров |
Вариант № 17.
| Работники | Номера работ | |||||
| Володин | ||||||
| Ганшин | ||||||
| Попов | ||||||
| Сидоров | ||||||
| Хаджиев | ||||||
| Зорин |
Вариант № 18.
| Работники | Номера работ | |||||
| Чертков | ||||||
| Демичев | ||||||
| Фурцева | ||||||
| Токин | ||||||
| Столяров | ||||||
| Носов |
Вариант № 19.
| Работники | Номера работ | |||||
| Суслов | ||||||
| Ларин | ||||||
| Выгонова | ||||||
| Петров | ||||||
| Васин | ||||||
| Титов |
Вариант № 20.
| Работники | Номера работ | |||||
| Беляев | ||||||
| Сидоров | ||||||
| Ваничкин | ||||||
| Зайцева | ||||||
| Ватагин | ||||||
| Родин |
Вариант № 21.
| Работники | Номера работ | |||||
| Шорин | ||||||
| Волков | ||||||
| Чайников | ||||||
| Летвинов | ||||||
| Дорина | ||||||
| Быкова |
Вариант № 22.
| Работники | Номера работ | |||||
| Скляров | ||||||
| Данин | ||||||
| Панина | ||||||
| Шолохов | ||||||
| Власенко | ||||||
| Сытин |
Вариант № 23.
| Работники | Номера работ | |||||
| Тыквин | ||||||
| Болшев | ||||||
| Строгина | ||||||
| Жданов | ||||||
| Чёрный | ||||||
| Ногина |
Вариант № 24.
| Работники | Номера работ | |||||
| Костина | ||||||
| Кузнецов | ||||||
| Швындин | ||||||
| Петров | ||||||
| Сидоров | ||||||
| Иваненко |
Вариант № 25.
| Работники | Номера работ | |||||
| Никитин | ||||||
| Коткова | ||||||
| Равин | ||||||
| Глатерман | ||||||
| Чуйкова | ||||||
| Санченко |
Вариант № 26.
| Работники | Номера работ | |||||
| Сеченов | ||||||
| Кудрявцев | ||||||
| Попкова | ||||||
| Танин | ||||||
| Воловик | ||||||
| Пьянова |
Вариант № 27.
| Работники | Номера работ | |||||
| Иванов | ||||||
| Петров | ||||||
| Сидоров | ||||||
| Васин | ||||||
| Лорин | ||||||
| Борисова |
Вариант № 28.
| Работники | Номера работ | |||||
| Вырин | ||||||
| Карина | ||||||
| Рожнев | ||||||
| Суслова | ||||||
| Пинкин | ||||||
| Лапин |
Вариант № 29.
| Работники | Номера работ | |||||
| Анукин | ||||||
| Павлова | ||||||
| Динченко | ||||||
| Волохов | ||||||
| Ританин | ||||||
| Бобова |
Вариант № 30.
| Работники | Номера работ | |||||
| Говорухин | ||||||
| Панюшкин | ||||||
| Попков | ||||||
| Ратникова | ||||||
| Капин | ||||||
| Мастерова |
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Решение задач оптимизации
Команда Сервис ® Поиск решения… предоставляет пользователю следующие возможности:
· поиск безусловных экстремумов функции одного или нескольких аргументов;
· поиск экстремумов функции одного или нескольких аргументов при наличии ограничений на найденное решение;
· поиск аргументов, при которых функция примет нулевое значение;
· выбор метода решения поставленной задачи;
· ввод ограничений на точность и время выполнения задачи.
Эти возможности реализуются с помощью параметров, собранных в основном окне Поиск решения и дополнительном – Параметры поиска решения. Дополнительное окно вызывается кнопкой <Параметры> из основного. Кнопка <Справка> вызывает окно с разъяснением смысла каждого параметра и возможностей, которые предоставляются при его заказе.
Безусловная нелинейная оптимизация используется, например, при выборе оптимальной функции для описания опытных данных (см. подразд. 6.8). Ее можно применять также для решения системы нелинейных уравнений. Для этого из уравнений системы
f1(x1, x2, …, xn) = 0; f2(x1, x2, …, xn) = 0; …. fn(x1, x2, …, xn) = 0
составляют вспомогательную целевую функцию
S = f12 + f22 + … fn2.
S – неотрицательная функция. Ее минимальное значение равно нулю и достигается только тогда, когда все слагаемые одновременно равны нулю. А это и есть решение исходной задачи.
Рассмотрим в качестве примера систему двух нелинейных уравнений
x2 + y2 = 3; 2x + 3y = 1.
Введем исходные данные по плану, представленному в табл. 6.7.1. Для удобства дальнейшей работы можно провести форматирование введенной информации.
Таблица 6.7.1
| Ячейки | Информация | Значение |
| А1 | Заголовок расчета | Решение системы нелинейных уравнений |
| А2 | Заголовок | Переменные |
| А3:В3 | Название переменных | А3: Х, В3: Y |
| А4:В4 | Начальные значения переменных | А3: 1, В3: –1 |
| А5 | Заголовок | Функции системы |
| А6:В6 | Названия функций системы | А6: f1, B6: f2 |
| А7:В7 | Формулы для расчета функций | =A4^2+B4^2–3 =2*A4+3*B4–1 |
| А8 | Заголовок | Вспомогательная целевая функция |
| А9 | Формула целевой функции | =A7^2+B7^2 |
Вызовем команду Сервис ® Поиск решения… В окне Поиск решения установим следующие параметры:
· "Установить целевую ячейку:" А9;
· "Равной:" минимальному значению;
· "Изменяя ячейки:" А4:В4;
· нажмем кнопку <Параметры> и в дополнительном окне Параметры поиска решения проверим, что флажок "Линейная модель" не установлен. Закроем дополнительное окно кнопкой <ОК>;
· запустим команду кнопкой <Выполнить> основного окна.
Когда команда закончит работу, на экране автоматически появляется окно Результаты поиска решения. Пояснения к параметрам, представленным в нем, вызываются кнопкой <Справка>. Закажем, к примеру, параметры "Сохранить найденное решение" и "Тип отчета: результаты". В этом случае начальные значения переменных в ячейках А4:В4 заменятся на найденные и в таблицу будет вставлен новый лист "Отчет по результатам 1". Просмотрите отчет. Проверьте, какое значение приняла вспомогательная целевая функция в А9 при найденных решениях. Если она существенно отличается от нуля, то решение найдено неверно.
Успешность поиска решения во многом зависит от выбора начального приближения переменных. В случае двух уравнений с двумя переменными можно не делать аналитического исследования функций системы, а составить таблицу вспомогательной целевой функции S (см. подразд. 3.2) и выбрать в качестве начального приближения те комбинации аргументов, при которых S принимает наименьшие значения.
Задание
Составьте таблицу значений целевой функции
S = (x2 + y2 –3)2 + (2x + 3y – 1)2
в диапазоне аргументов –3 < x < 3, – 3 < y < 3. Выберите 4–5 точек с наименьшими значениями функции, проведите поиск минимума, используя каждую из них в качестве начального приближения. В результате должно быть получено только два разных решения: х1 = –1,268; у1 = 1,179 и х2 = 1, 576; у2 = –0,717. Графически уравнения системы представляются окружностью и прямой линией. Система такого типа не может иметь больше двух точек пересечения.
Задачи технического и экономического планирования часто решаются методами линейного программирования. Особенность этих задач – большое количество исходных данных. Чтобы упорядочить их, полезно перед вводом данных в ЭВМ составить математическую модель задачи на бумаге. При этом можно руководствоваться следующим планом:
1. Выбираем критерий оптимизации, т. е. показатель, по которому будут сравниваться разные планы, и планируемые параметры, т. е. те показатели, которыми можно манипулировать при выборе оптимального плана. Набор конкретных значений планируемых параметров называют планом.
2. Определяемся с целью оптимизации, т. е. решаем, минимальное или максимальное значение критерия будет соответствовать наилучшему плану.
3. Составляем целевую функцию, т. е. записываем с помощью формул алгоритм, по которому можно рассчитать критерий для любого плана.
4. Составляем формулы ограничений, которые показывают, какие планы имеет смысл рассматривать при выборе оптимального.
Только после составления математической модели имеет смысл вводить информацию в ЭВМ.
Пример
Процесс изготовления двух видов изделий состоит в последовательной обработке каждого из них на трех станках. Возможности использования каждого из них ограничены 10-ю часами в сутки. Удельное время обработки и удельная прибыль для каждого изделия приведены в табл.6.7.2. Найти оптимальный план выпуска каждого изделия.
Таблица 6.7.2
| Изделие | Время обработки одного изделия, мин | Прибыль на одно изделие, $ | ||
| Станок 1 | Станок 2 | Станок 3 | ||
| A | ||||
| B |
Составляем модель по предложенному выше плану:
1. Критерий оптимизации – общая прибыль (ОП), планируемые параметры – число запланированных к выпуску изделий каждого вида (kA, kВ).
2. Цель оптимизации – максимальная прибыль.
3. Целевая функция – ОП = kAПА + kBПВ, где ПА и ПВ – удельные прибыли от продажи каждого вида изделий.
4. Ограничения – в этой задаче наложены ограничения только по времени использования в трудовом процессе каждого станка:
· Станок 1: tA1kA + tB1kB <= 600;
· Станок 2: tA2kA + tB2kB<= 600;
· Станок 3: tA3kA + tB3kB<= 600.
Здесь индексы показывают, какому станку и изделию соответствует удельная норма времени обработки. Например, tB2 – норма времени обработки одного изделия В на станке 2.
На рис. 6.7.1 изображен пример расположения модели на рабочем листе Excel.
| A | B | C | D | E | F | G | |||
| Изделие | Время обработки одного изделия, мин | Удельная прибыль | План выпуска изделий | Ожидаемая прибыль | |||||
| Станок 1 | Станок 2 | Станок 3 | |||||||
| A | $2 | ||||||||
| B | $3 | ||||||||
| Время по плану | Общая прибыль | ||||||||
| Допустимое время | |||||||||
Рис. 6.7.1
В ячейки F3, F4 вводится ориентировочный план. Можно оставить их пустыми. В ячейки G3, G4 вводятся формулы прибыли по каждому виду изделий, в ячейке G5 эти прибыли суммируются. В ячейки B5:D5 вводятся левые части формул ограничений.
После того, как все элементы модели занесены на рабочий лист, можно вызывать команду Сервис ® Поиск решения… В ее диалоговом окне для нашего примера следует установить такие значения параметров:
· "Установить целевую ячейку" – G5 (ячейка, в которой находится окончательное значение целевой функции).
· "Равной" – максимальному значению.
· "Изменяя ячейки" – F3:F4 (ячейки, в которых находятся планируемые параметры. После окончания работы команды в них будут записаны оптимальные значения).
· "Ограничения" – для заполнения этого окна надо нажать кнопку <Добавить>. В появившемся окне Добавление ограничения три поля. В левом указывают адрес ячейки, в которой сосчитана та часть ограничения, которая меняет значение для разных планов. В правом – должна стоять константа, с которой сравнивается значение левого поля при разных планах. Если она уже введена на рабочий лист, здесь можно указать ее адрес. Для нашего примера в левое поле вводим В5, в правое – В6, в центральном поле устанавливаем соотношение <=. Нажимаем кнопку <Добавить>. Повторяем аналогичные действия для ввода ограничений по второму и третьему станкам. После установки последнего ограничения вместо кнопки <Добавить> нажимают <ОК>. Если какие-то ограничения оказались лишними или введены неверно, это можно исправить кнопками<Удалить> и <Изменить>.
· Нажимаем кнопку <Параметры>. Появляется диалоговое окно Параметры поиска решения. Здесь оговариваются метод и точность решения. Для задач линейного программирования достаточно установить только параметры "Линейная модель" и "Неотрицательные значения", закрыть окно кнопкой <ОК> и нажать кнопку <Выполнить>.
После окончания расчетов команда выдает окно Результаты поиска решения. Реплика, которая помещена в него, либо подтверждает успешность решения, либо предупреждает, что оптимальное решение не найдено. В этом случае надо проверить, правильно ли составлена и введена модель.
Похожие статьи:
poznayka.org
18 Распределительная задача. Задача о назначениях (минимизация затрат времени на выполнение работ).
Требуется осуществить монтаж п-ого количества объектов (i). Для этого имеется п монтажных бригад(j).Известна ориентировочная длительность монтажа каждого из объектов каждой из бригад:
|
| ||||
| С= |
|
| ……. |
|
| ………………………………… | ||||
|
|
| …….. |
| |
На один объект назначается только одна бригада. Требуется так распределить бригады по объектам, чтобы суммарная длительность монтажа была минимальной
W=
Ограничения:
закрепление за каждым из объектов одной бригады:
(i=1÷n)
закрепление каждой из бригад только за одним объектом:
(j=1÷n)
или
19 Алгоритм решения задачи целочисленного программирования.
С математической точки зрения данные задачи – это частный случай транспортной задачи. В таких задачах от каждого поставщика к каждому потребителю поставляется одна единица груза.Например. Только одного рабочего можно назначить для выполнения данной работы, или одна операция может выполнятся только на одном из станков. Поэтому все “запасы” и все “заказы” =1. Все переменные решения в таких задачах могут принимать значения только 1 или 0. Эффективным методом решения явл-ся алгоритм транспортной задачи.
На п-станках (і) различных типов можно выполить п-операций (ј).
За каждым из станков м.б. закреплена лишь одна операция и одна и та же операция м. выполниться только одним из станков. Время выполнения каждой из операций на каждом из станков задается матрицей:
|
|
| ……. |
| |
| С= |
|
| ……. |
|
| ……………………………… | ||||
|
|
| …….. |
| |
Составив такое распределение выполняемых операций м-ду станками, при кот. суммарные затраты времени на обработку детали является минимальным.
W=
Ограничения:
закрепление за каждым станком i только одной операции j:
(i=1÷n)
Закрепление каждой из операций только за одним станком :
(j=1÷n)
или
20 Метод дихотомии в поиске экстремума функции одной переменной.
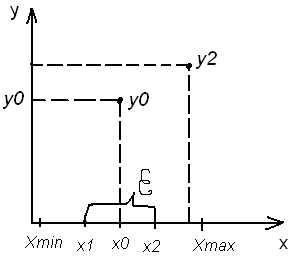
1 этап: Вычисляется значение целевой функции в 2-ух точках х1 и х2 расположенных симметрично относительно середины диапазона варьирования переменной х.
Середина диапазона варьирования переменной х определяется по формулу:
;
Разность между значениями переменной х, а х2 – х1 обозначим через
Значения переменной х в каждом из поставленных опытов будет:
Величина выбирается как можно меньшей, но достаточной для того, чтобы можно было различить результаты опытов. ( Хmin до Х1 отбрасывается)
2-ой этап: Аналогично планируется постановка очередных 2-ух опытов вблизи центра.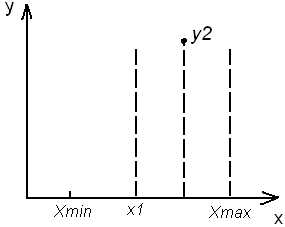
24 Методы решения задач целочисленного програмированния. Области применения.С математической точки зрения данные задачи – это частный случай транспортной задачи. В таких задачах от каждого поставщика к каждому потребителю поставляется одна единица груза.
Например. Только одного рабочего можно назначить для выполнения данной работы, или одна операция может выполнятся только на одном из станков. Поэтому все “запасы” и все “заказы” =1. Все переменные решения в таких задачах могут принимать значения только 1 или 0. Эффективным методом решения явл-ся алгоритм транспортной задачи.
На п-станках (і) различных типов можно выполить п-операций (ј).
За каждым из станков м.б. закреплена лишь одна операция и одна и та же операция м. выполниться только одним из станков. Время выполнения каждой из операций на каждом из станков задается матрицей:
Составив такое распределение выполняемых операций м-ду станками, при кот. суммарные затраты времени на обработку детали является минимальным.
W=
Ограничения:
закрепление за каждым станком i только одной операции j:
(i=1÷n)
Закрепление каждой из операций только за одним станком :
(j=1÷n)
или
studfiles.net
Задача оптимизации плана производства
Пример. Для производства трех видов продукции предприятие использует два типа технологического оборудования и два вида сырья. Нормы затрат сырья и времени на изготовление одного изделия каждого вида приведены в таблице. В ней же указаны общий фонд рабочего времени каждой из групп технологического оборудования, объемы имеющегося сырья каждого вида, а также цена одного изделия данного вида и ограничения на возможный выпуск каждого из изделий.
| Ресурсы | Нормы затрат на одно изделие вида | Общее количество ресурсов | ||
| 1 | 2 | 3 | ||
| Производительность оборудования (нормо-ч) 1 типа 2 типа | 2 4 | – 3 | 4 1 | 200 500 |
| Сырье (кг) 1 вида 2 вида | 10 30 | 15 20 | 20 25 | 1495 4500 |
| Цена одного изделия (руб.) | 10 | 15 | 20 | – |
| Выпуск (шт) минимальный максимальный | 10 20 | 20 40 | 25 100 | – |
Составить такой план производства продукции, согласно которому будет изготовлено необходимое количество изделий каждого вида, а общая стоимость всей изготовляемой продукции максимальна.
РЕШЕНИЕ. Составим математическую модель. Предположим, что предприятие изготовит х1 изделий 1-го вида, х2 изделий 2-го вида и х3изделий 3-го вида.
Задача состоит в определении максимальной общей стоимости всей изготовляемой продукции.
,
при ограничениях на имеющийся фонд рабочего времени каждого типа оборудования:
,
,
на возможное использование сырья:
,
,
на возможный выпуск изделий каждого вида:
, ,.
Результаты решения задачи с помощью пакета прикладных программ POM WIN содержатся в таблицах 1-3 (стр.19‑20).
Из таблиц 1 и 3 следует, что оптимальный план выпуска продукции включает в себя 10 изделий 1-го вида, 33 изделия 2-го вида и 45 изделий 3-го вида. Максимальная общая стоимость продукции составляет 1495 рублей. При этом рабочее время станков 1 типа использовано полностью (slack 1 = 0), 316 часов работы станков 2 типа остались неиспользованными (slack 2 = 316). Сырье 1-го вида использовано полностью (slack 3 = 0), остаток сырья 2-го вида составляет 2415 кг (slack 4 = 2415).
Оптимальное решение останется тем же самым, если цены изделий будут изменяться в пределах, указанных в таблице 2. В частности, цены изделий первого и второго вида могут быть как угодно снижены, а цена изделия третьего вида как угодно повышена.
Так как базисными переменными (таблица 3) являются 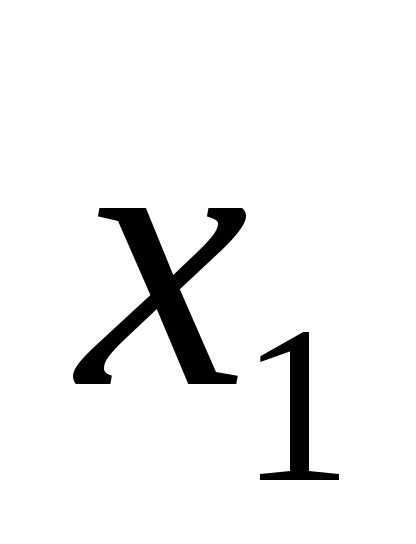 ,
,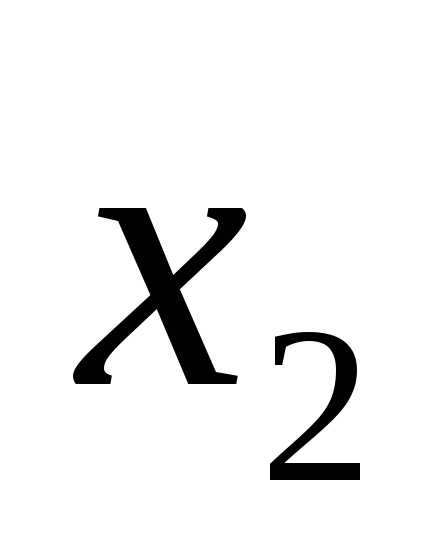 ,
,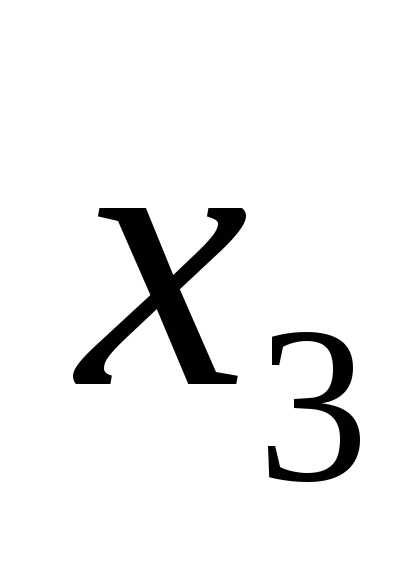 ,slack 2 (остаток рабочего времени станков 2 типа), slack 4 (остаток сырья 2-го вида), slack 6, slack 8, slack 10 (разность между верхней границей выпуска продукции 1-го, 2-го и 3-го видов соответственно и оптимальным значением выпуска), и surplus7, surplus 9 (превышение плана выпуска продукции по сравнению с нижней границей), то оптимальное решение задачи определяется из следующей системы уравнений.
,slack 2 (остаток рабочего времени станков 2 типа), slack 4 (остаток сырья 2-го вида), slack 6, slack 8, slack 10 (разность между верхней границей выпуска продукции 1-го, 2-го и 3-го видов соответственно и оптимальным значением выпуска), и surplus7, surplus 9 (превышение плана выпуска продукции по сравнению с нижней границей), то оптимальное решение задачи определяется из следующей системы уравнений.
,
,
,
,
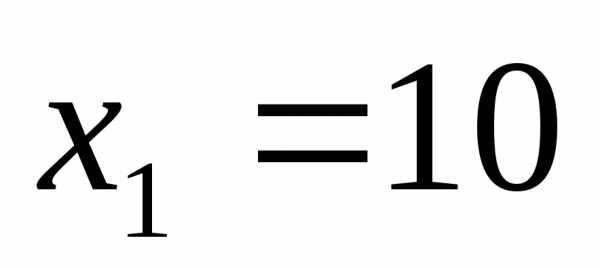 , (1)
, (1)
,
,
,
,
.
При изменении общего количества ресурсов сырья и ресурсов станков, а также границ выпуска продукции в пределах, указанных в таблице 2, решение задачи будет изменяться, при этом оптимальное решение будет определяться системой (1) с измененными правыми частями.
Анализ двойственных оценок (таблица 1 или таблица 2) показывает, что если запасы ресурсов сырья 1-го вида увеличить на единицу (уменьшить на единицу), то оптимальное значение целевой функции увеличится на единицу (уменьшится на единицу). Изменения фонда рабочего времени станков, запасов сырья 2-го вида, границ выпуска изделий в указанных в таблице 2 пределах, не влияют на оптимум задачи, то есть на максимальное значение прибыли.
studfiles.net
4. Задача об использовании мощностей (задача о загрузке оборудования)
Предприятию задан план производства m видов продукции по времени и номенклатуре: требуется за время Т выпустить bi (i=1,…,m) единиц продукции каждого типа. Продукция производится на станках n типов. Для каждого станка известны производительность aij(то есть, количество продукции j-го вида, которое можно произвести на станке i-го типа) и затраты cij на изготовление продукции j-го вида на станке i-го типа в единицу времени.
Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.
Обозначим xij – время, в течение которого станок i-го типа будет занят изготовлением продукции j-го вида (i = 1,…, m; j = 1,…, n).
Затраты на производство всей продукции выразятся функцией F = 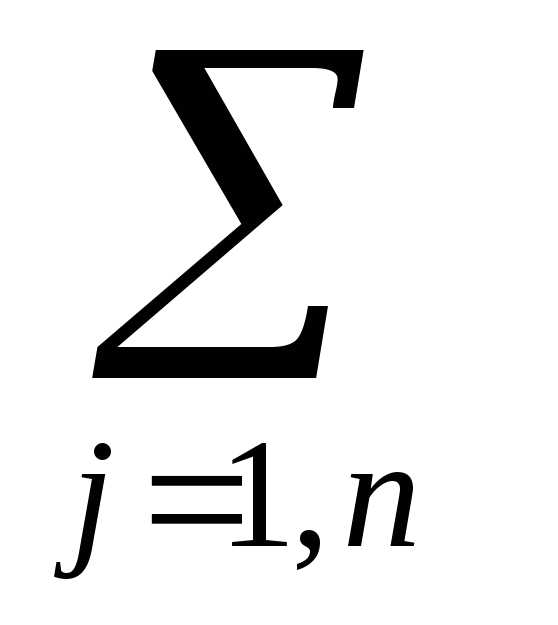
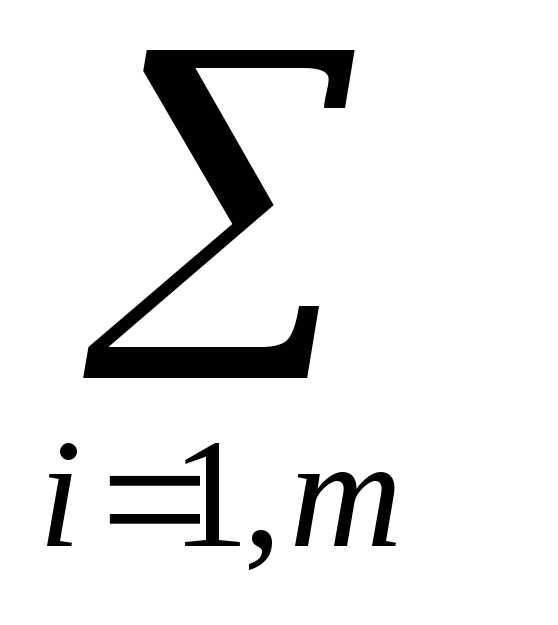 cijּxij, которую нужно минимизировать.
cijּxij, которую нужно минимизировать.
Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства: 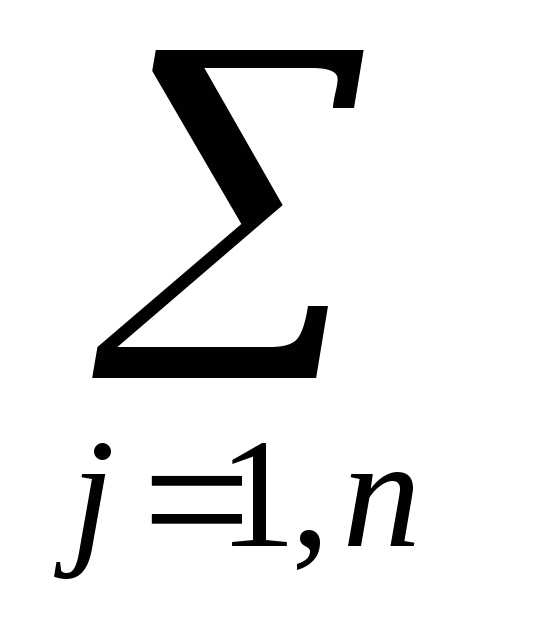 aijּxij = bi(i=1,…,n).
aijּxij = bi(i=1,…,n).
Кроме того, xij≥ 0 (i = 1,…,m; j = 1,…, n).
Так как время работы каждого станка ограничено и не превышает Т, то система ограничений может быть дополнена неравенствами:
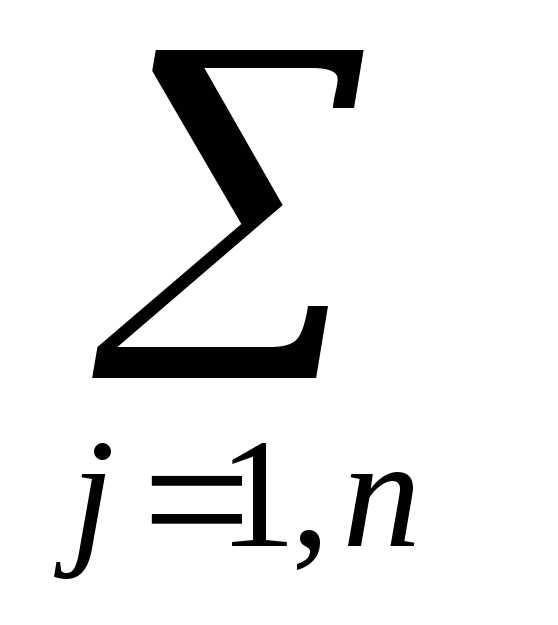 xij≤ T (i = 1,…, n).
xij≤ T (i = 1,…, n).
5. Задача о раскрое материалов.
На раскрой (распил, обработку) поступает материал одного образца в количестве A единиц. Требуется изготовить из него m разных комплектующих изделий в количествах, пропорциональных числам bi (i = 1,…, m) – условие комплектности.
Каждая единица материала может быть раскроена n различными способами, причем использование j-го способа (j = 1,…, n) дает aij единиц i-го изделия (i = 1,…, m).
Необходимо найти план раскроя, обеспечивающее максимальное количество комплектов.
Обозначим xj – число единиц материала, раскраиваемых j-ым способом,
x – число изготавливаемых комплектов изделий.
Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то 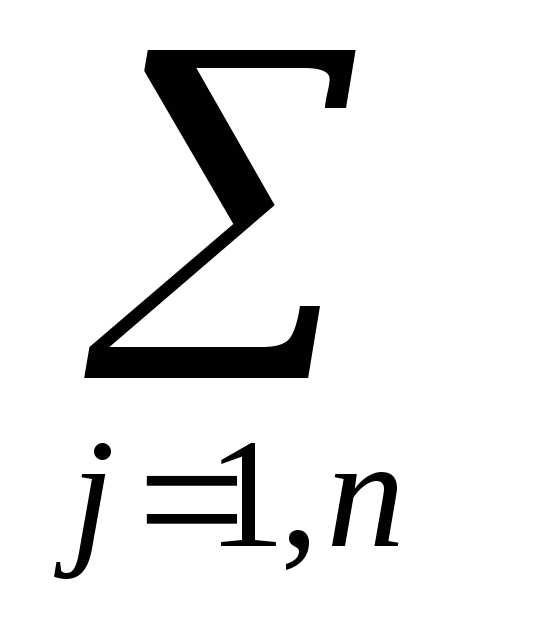 xj= A.
xj= A.
Требование комплектности выразится уравнениями
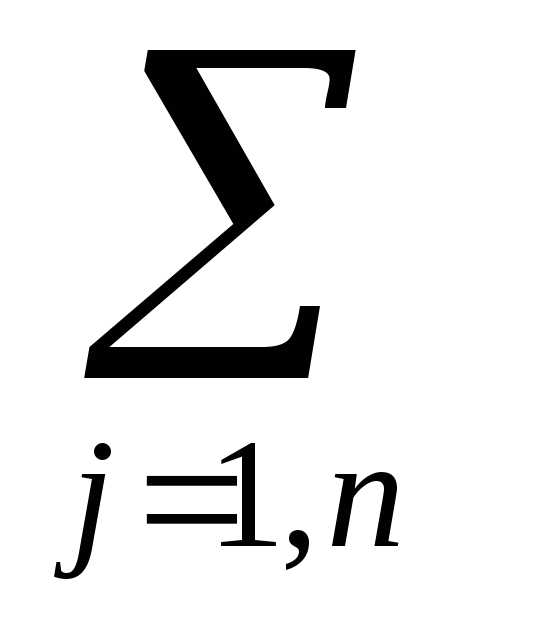 xjּaij = biּx (i = 1,…, m)
xjּaij = biּx (i = 1,…, m)
Кроме того xj≥ 0 (j = 1,…, n).
2.2.8. Практический блок Пример
Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
1. По данным, приведенным в таблице 2.2.3 составить систему математических зависимостей (неравенств) и целевую функцию.
Изобразить геометрическую интерпретацию задачи и найти оптимальное решение.
Провести аналитическую проверку и определить значение целевой функции.
Определить избытки ресурсов.
Вычислить объективно обусловленные оценки.
Исследовать устойчивость решения.
Таблица 2.2.3 – Матрица удельных нормативов.
| Продукция | Сырье | Прибыль на одно изделие | ||
| Рес. 1 | Рес. 2 | Рес. 3 | ||
| I. Изделие 1 | 2.4 | 8.0 | 6.2 | 50 ( |
| II. Изделие 2 | 12.2 | 5.4 | 2.2 | 40 ( |
| Наличие ресурсов | 500 | 470 | 340 | – |
Решение:
1. Обозначим:
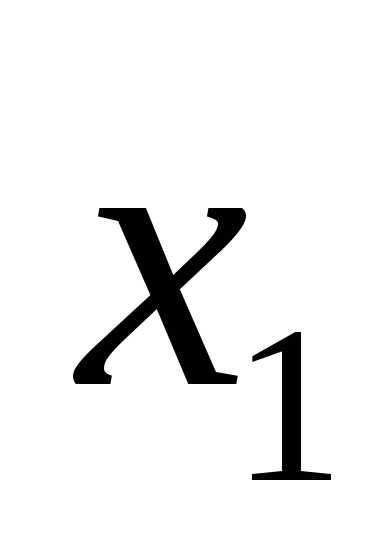 –объем изделия 1;
–объем изделия 1;
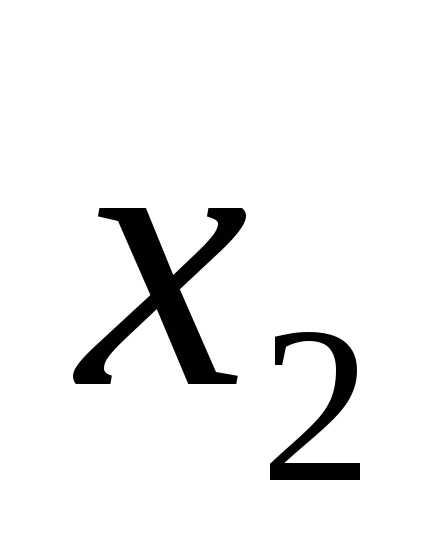 –объем изделия 2.
–объем изделия 2.
Опишем модель с помощью системы неравенств линейных уравнений:
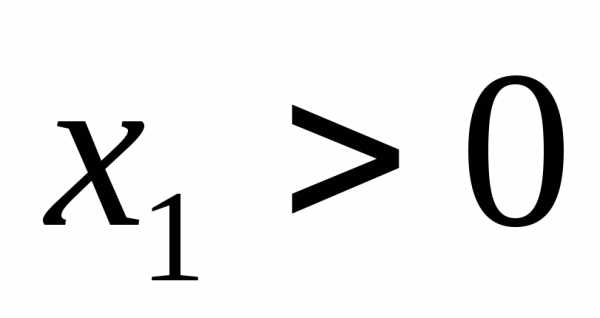
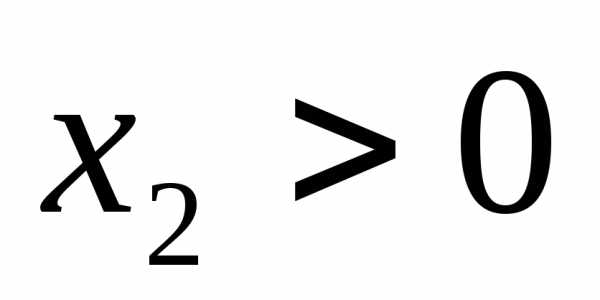 ;
;
;
;
;
–целевая функция (критерий оптимальности).
studfiles.net
РАБОТА №7. ОПТИМИЗАЦИЯ ЗАМЕНЫ ОБОРУДОВАНИЯ НА ПРЕДПРИЯТИИ — МегаЛекции
Важной экономической проблемой является своевременное обновление оборудования: автомобилей, станков, телевизоров и т. п. Старение оборудования включает физический и моральный износ, в результате чего растут затраты на ремонт и обслуживание, снижается производительность труда и ликвидная стоимость. Задача заключается в определении оптимальных сроков замены старого оборудования. Критерием оптимальности являются доход от эксплуатации оборудования (задача максимизации) либо суммарные затраты на эксплуатацию в течение планируемого периода (задача минимизации).
Предположим, что планируется эксплуатация оборудования в течение некоторого периода времени продолжительностью N лет. Оборудование имеет тенденцию с течением времени стареть и приносить все меньший доход R(T) (T – возраст оборудования). При этом есть возможность в начале любого года продать устаревшее оборудование за цену S(T), которая также зависит от возраста T, и купить новое оборудование за цену P. Под возрастом оборудования понимается период эксплуатации оборудования после последней замены, определенный в годах. Требуется найти оптимальный план замены оборудования с тем, чтобы суммарный доход за все N лет был максимальным, учитывая, что к началу эксплуатации возраст оборудования составлял T=0 лет.
Исходными данными в задаче являются доход r(t) от эксплуатации в течение одного года оборудования возраста t лет, остаточная стоимость S(t), цена нового оборудования P и начальный возраст оборудования T0.
Таблица 7.1
| T | … | N | ||
| R | R(0) | R(1) | … | R(n) |
| S | S(0) | S(1) | … | S(N) |
При составлении динамической модели выбора оптимальной стратегии обновления оборудования процесс замены рассматривается как N-шаговый, т. е. период эксплуатации разбивается на N-шагов.
Выберем в качестве шага оптимизацию плана замены оборудования с K-го по N-й годы.
Очевидно, что доход от эксплуатации оборудования за эти годы будет зависеть от возраста оборудования к началу рассматриваемого шага, т. е. K-го года.
Поскольку процесс оптимизации ведется с последнего шага (K = N), то на K-м шаге неизвестно, в какие годы с первого по (K – 1)-й должна осуществляться замена и соответственно неизвестен возраст оборудования к началу K-го года. Возраст оборудования, который определяет состояние системы, обозначим T. На величину T накладывается следующее ограничение:
(7.1)
Выражение (7.1) свидетельствует о том, что T не может превышать возраст оборудования за (K – 1)-й год его эксплуатации с учетом возраста к началу первого года, который составляет T0 лет; и не может быть меньше единицы (этот возраст оборудование будет иметь к началу K-го года, если замена произошла в начале предыдущего (K – 1)-го года).
Таким образом, переменная T в данной задаче является переменной состояния системы на K-м шаге.
Переменной управления на K-м шаге является логическая переменная, которая может принимать одно из двух значений: сохранить (C) или заменить (З) оборудование в начале K-го года:
Функцию Беллмана Fk(T) определяют как максимально возможный доход от эксплуатации оборудования за годы с K-го по N-й, если к началу K-го возраст оборудования составлял T лет. Применяя то или иное управление, система переходит в новое состояние. Так, например, если в начале K-го года оборудование сохраняется, то к началу (K + 1)-го года его возраст увеличится на единицу (состояние системы станет T+1), в случае замены старого оборудования новое достигнет к началу (K + 1)-го года возраста T1 = 1 год.
На этой основе можно записать уравнение, которое позволяет рекуррентно вычислить функцию Беллмана, опираясь на результаты предыдущего шага. Для каждого варианта управления доход определяется как сумма двух слагаемых – непосредственного результата управления и его последствий.
Если в начале каждого года сохраняется оборудование, возраст которого T лет, то доход за этот год составит R(T). К началу (K + 1)-го года возраст оборудования достигнет (T + 1) и максимально возможный доход за оставшиеся годы (с (K + 1)-го по N-й) составит Fk+1(T+1). Если в начале K-го года принято решение о замене оборудования, то продается старое оборудование возраста Tлет по цене S(T), приобретается новое за P единиц, а его эксплуатация в течение K-го года нового оборудования принесет прибыль R(0). К началу следующего года возраст оборудования составит 1 год и за все оставшиеся годы с (K + 1)-го по N-й максимально возможный доход будет Fk+1(1). Из двух возможных вариантов управления выбирается тот, который приносит максимальный доход. Таким образом, уравнение Беллмана на каждом шаге управления имеет вид
(7.2)
Функция Fk(T) вычисляется на каждом шаге управления для всех . Управление, при котором достигается максимум дохода, является оптимальным.
Для первого шага условной оптимизации при k = n функция представляет собой доход за последний n-й год:
(7.3)
Значения функции Fn(T), определяемые Fn-1(T), Fn-2(T) вплоть до F1(T). F1(T0) представляют собой возможные доходы за все годы. Максимум дохода достигается при некотором управлении, применяя которое на первом году, мы определяем возраст оборудования к началу второго года. Для данного возраста оборудования выбирается управление, при котором достигается максимум дохода за годы со второго по N-й и т. д. В результате на этапе безусловной оптимизации определяются годы, в начале которых следует произвести замену оборудования.
Пример. Найти оптимальную стратегию эксплуатации оборудования на период продолжительностью 6 лет, если годовой доход r(t) и остаточная стоимость S(t) в зависимости от возраста заданы табл. 27, стоимость нового оборудования равна P = 13, а возраст оборудования к началу эксплуатационного периода составлял 1 год.
Таблица 7.2
Решение. 1 этап. Условная оптимизация.
1-й шаг. K = 6. Для первого шага возможные состояния системы t = 1, 2, …, 6. Функциональное управление имеет вид (31).
2-й шаг. K = 5. Для второго шага возможные состояния системы t = 1, 2, …, 5. Функциональное уравнение имеет вид
3-й шаг. K = 4.
4-й шаг. K = 3.
5-й шаг. K = 2.
6-й шаг. K = 1.
2-й этап. Безусловная оптимизация.
Безусловная оптимизация начинается с шага при K = 1. Максимально возможный доход от эксплуатации оборудования за годы с 1-го по 6-й составляет F1(1) = 37. Этот оптимальный выигрыш достигается, если на первом году не производить замены оборудования. Тогда к началу второго года возраст оборудования увеличится на единицу и составит: T2 = T1 + 1 = 1 + 1 = 2. Безусловно, оптимальное управление при K=2, Х2(2) = С, т. е. максимум дохода за годы со 2-го по 6-й достигается, если оборудование не заменяется.
К началу третьего года при k=3 возраст оборудования станет: T3 = T2 + 1 = 3. Безусловное оптимальное управление Х3(3) = З, т. е. для получения максимума прибыли за оставшиеся годы необходимо провести замену оборудования.
К началу четвертого года при K=4 возраст оборудования станет равен T4=1. Безусловное оптимальное управление Х4(1) = С.
Далее соответственно:
Таким образом, за 6 лет эксплуатации оборудования замену надо произвести один раз – в начале третьего года эксплуатации.
Пример. Задачу нахождения кратчайшего пути можно применить для оптимизации затрат на оборудование в течение определенного времени. В этом году предприятию предстоит решить, приобрести ли новый дорогой станок с низкими первоначальными расходами на обслуживание или продолжать использовать приобретенный ранее станок с высокими расходами на обслуживание.
Данную задачу решаем в MicrosoftOfficeExcel (рис.7.1). Стоимостные параметры заданы в ячейках Н2:Н7. Предположим, что расходы составляют $ 1 600 000 на приобретение оборудования и $ 500 000 на его обслуживание в год приобретения; для каждого дополнительного года эксплуатации ежегодные затраты на обслуживание составляют $ 1 000000, $ 1 500 000 и $ 2 200 000. Для простоты предположим, что период планирования в модели составляет четыре года. Обозначим черезс расходы на приобретение нового оборудования в начале года j (j = 1, 2, 3, 4) и обслуживание его до начала года j (j = 2, 3, 4, 5). Если оборудование может работать только до начала года j, где j< 5, то в начале года j необходимо снова приобретать новое оборудование.
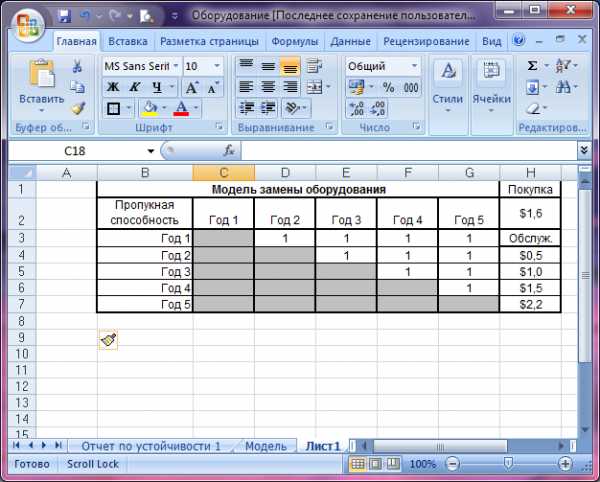
Рис. 7.1 - Исходные данные модели замены оборудования
Рассмотрим три возможных варианта поведения.
1) Приобретать новое оборудование в начале каждого года. Такая политика приведет к самым высоким расходам на приобретение и минимальным расходам на обслуживание. Общие расходы на приобретение и обслуживание в таком случае составят C12 + C23 + C34 + C45.
2) Приобрести новое оборудование только в начале первого года, а затем заниматься его ремонтом и обслуживанием в течение последующих лет. При такой политике суммарные расходы на приобретение будут минимальны, а расходы на обслуживание максимальны. Общие расходы на приобретение и обслуживание составят C15.
3) Новое оборудование приобретается в начале 1 и 4 годов. Суммарные расходы составят C14 + C45.
Из всех возможных вариантов предприятие хочет выбрать вариант с минимальными суммарными затратами. Чтобы решить эту задачу, необходимо найти кратчайший путь (в данном случае — путь с минимальными затратами) из узла 1 в узел 5 для сети, показанной на рисунке 3.2. Каждый узел на кратчайшем пути означает замену оборудования в соответствующем году, т.е. в этом году необходимо приобрести новое оборудование.
Составим таблицу, где будут видны удельные затраты по покупке нового оборудования и его дальнейшего обслуживания (рис.7.2).
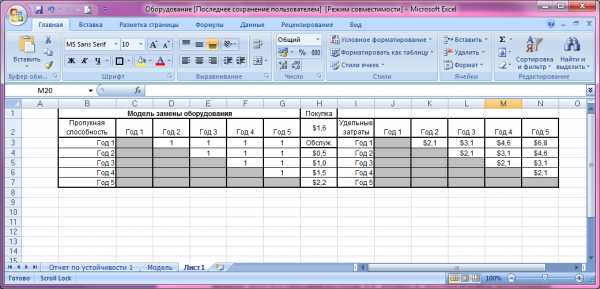
Рис.7.2 Нахождение удельных затрат по покупке нового оборудования и его дальнейшего обслуживание
В ячейках J3:N6 вычислены затраты на покупку и обслуживание станка, если он приобретен в одном году и эксплуатируется до начала другого указанного года, т.е.
- ячейка K3= h3+h5 (стоимость покупки + обслуживание со следующего года после покупки)
- ячейка L3= K3+H5 (удельные затраты +обслуживание 3 года) и т.д.
Теперь после расчета удельных затрат по каждому году, мы можем выяснить, когда лучше покупать новое оборудование и каковы будут наши затраты (рис.7.3).
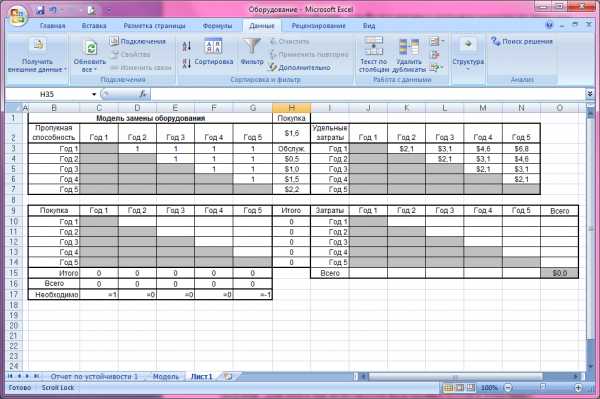
Рис.7.3 Подготовительная таблица для расчета оптимальных закупок
Ячейки переменных решения с серым фоном в диапазоне C10:G14 соответствуют невозможным решениям с обратным ходом событий (например, приобретение станка в году 3 для использования в году 1). Начальный и конечный годы использования оборудования отмечены в строке 17 с помощью чисел 1 и -1. В ячейках C3:G7 содержится матрица связей между узлами, а в ячейках J10:N14 вычислены расходы для решений, записанных в ячейках C10:G14. Теперь при помощи надстройки «Поиск решения» мы выберем оптимальный вариант с минимальными затратами (рис.7.4).
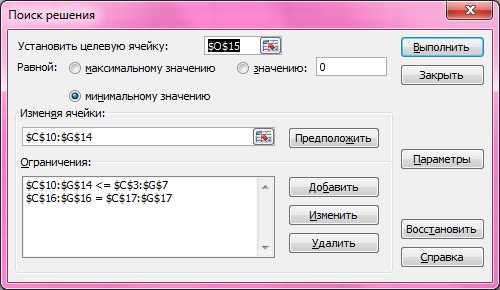
Рис.7.4 Надстройка «Поиск решений»
В данной надстройке, как видно на рис. 7.4. мы назначаем целевую ячейку, т.е. ячейку О15 (всего затрат на приобретение нового оборудования), которая должна иметь минимальное значение, изменяя ячейки С10:G14. Также мы устанавливаем некоторые ограничения:
Ячейки С10:G14 должны быть меньше либо равны ячейкам С3:G7. Покупка нового оборудования в данной модели должна быть меньше либо равна пропускная способности всех лет.
Ячейки С16:G16 должны быть равны ячейкам С17:G17. Всего количество покупок должно быть равно необходимому количеству покупок.
Задаём параметры в надстройке «Поиск решения» (рисунок 7.5).
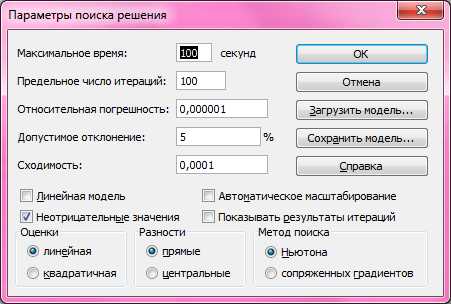
Рис.7.5 Параметры надстройки «Поиск решения»
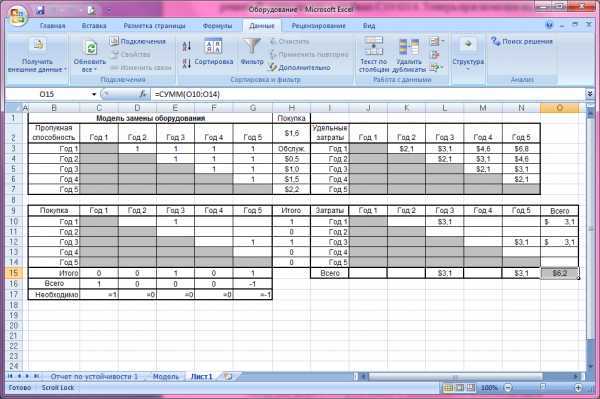
Рис. 7.6 – Результат выполнения работы
В данном случае оптимальной стратегией является приобретение нового станка в начале года 1, использование его в течение двух лет и замена в начале года 3 новым станком, который затем используется до начала года 5. При этом общие расходы за четыре года составят 6,2 млн. долл.
Варианты задания для выполнения работы
Вариант 1
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 2
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 3
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 4
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 5
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 6
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 7
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 8
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 9
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 10
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 11
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 12
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 13
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 14
| T | |||||||
| R(T) | |||||||
| S(Т) | |||||||
| Стоимость Обслуживания | - |
Вариант 15
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
6.7. Решение задач оптимизации
Команда Сервис Поиск решения… предоставляет пользователю следующие возможности:
поиск безусловных экстремумов функции одного или нескольких аргументов;
поиск экстремумов функции одного или нескольких аргументов при наличии ограничений на найденное решение;
поиск аргументов, при которых функция примет нулевое значение;
выбор метода решения поставленной задачи;
ввод ограничений на точность и время выполнения задачи.
Эти возможности реализуются с помощью параметров, собранных в основном окне Поиск решения и дополнительном – Параметры поиска решения. Дополнительное окно вызывается кнопкой <Параметры> из основного. Кнопка <Справка> вызывает окно с разъяснением смысла каждого параметра и возможностей, которые предоставляются при его заказе.
Безусловная нелинейная оптимизация используется, например, при выборе оптимальной функции для описания опытных данных (см. подразд. 6.8). Ее можно применять также для решения системы нелинейных уравнений. Для этого из уравнений системы
f1(x1,x2, …,xn) = 0;f2(x1,x2, …,xn) = 0; ….fn(x1,x2, …,xn) = 0
составляют вспомогательную целевую функцию
S = f12 + f22 + … fn2.
S– неотрицательная функция. Ее минимальное значение равно нулю и достигается только тогда, когда все слагаемые одновременно равны нулю. А это и есть решение исходной задачи.
Рассмотрим в качестве примера систему двух нелинейных уравнений
x2 + y2 = 3; 2x + 3y = 1.
Введем исходные данные по плану, представленному в табл. 6.7.1. Для удобства дальнейшей работы можно провести форматирование введенной информации.
Таблица 6.7.1
| Ячейки | Информация | Значение |
| А1 | Заголовок расчета | Решение системы нелинейных уравнений |
| А2 | Заголовок | Переменные |
| А3:В3 | Название переменных | А3: Х, В3: Y |
| А4:В4 | Начальные значения переменных | А3: 1, В3: –1 |
| А5 | Заголовок | Функции системы |
| А6:В6 | Названия функций системы | А6: f1, B6: f2 |
| А7:В7 | Формулы для расчета функций | =A4^2+B4^2–3 =2*A4+3*B4–1 |
| А8 | Заголовок | Вспомогательная целевая функция |
| А9 | Формула целевой функции | =A7^2+B7^2 |
Вызовем команду Сервис Поиск решения… В окне Поиск решения установим следующие параметры:
"Установить целевую ячейку:" А9;
"Равной:" минимальному значению;
"Изменяя ячейки:" А4:В4;
нажмем кнопку <Параметры> и в дополнительном окне Параметры поиска решения проверим, что флажок "Линейная модель" не установлен. Закроем дополнительное окно кнопкой <ОК>;
запустим команду кнопкой <Выполнить> основного окна.
Когда команда закончит работу, на экране автоматически появляется окно Результаты поиска решения. Пояснения к параметрам, представленным в нем, вызываются кнопкой <Справка>. Закажем, к примеру, параметры "Сохранить найденное решение" и "Тип отчета: результаты". В этом случае начальные значения переменных в ячейках А4:В4 заменятся на найденные и в таблицу будет вставлен новый лист "Отчет по результатам 1". Просмотрите отчет. Проверьте, какое значение приняла вспомогательная целевая функция в А9 при найденных решениях. Если она существенно отличается от нуля, то решение найдено неверно.
Успешность поиска решения во многом зависит от выбора начального приближения переменных. В случае двух уравнений с двумя переменными можно не делать аналитического исследования функций системы, а составить таблицу вспомогательной целевой функции S(см. подразд. 3.2) и выбрать в качестве начального приближения те комбинации аргументов, при которыхSпринимает наименьшие значения.
Задание
Составьте таблицу значений целевой функции
S = (x2 + y2 –3)2 + (2x + 3y – 1)2
в диапазоне аргументов –3 < x < 3, – 3 < y < 3. Выберите 4–5 точек с наименьшими значениями функции, проведите поиск минимума, используя каждую из них в качестве начального приближения. В результатедолжно быть получено только два разных решения:х1= –1,268;у1= 1,179 их2= 1, 576;у2= –0,717. Графически уравнения системы представляются окружностью и прямой линией. Система такого типа не может иметь больше двух точек пересечения.
Задачи технического и экономического планирования часто решаются методами линейного программирования. Особенность этих задач – большое количество исходных данных. Чтобы упорядочить их, полезно перед вводом данных в ЭВМ составить математическую модель задачи на бумаге. При этом можно руководствоваться следующим планом:
Выбираем критерий оптимизации, т. е. показатель, по которому будут сравниваться разные планы, ипланируемые параметры, т. е. те показатели, которыми можно манипулировать при выборе оптимального плана. Набор конкретных значений планируемых параметров называютпланом.
Определяемся с целью оптимизации, т. е. решаем, минимальное или максимальное значение критерия будет соответствовать наилучшему плану.
Составляем целевую функцию, т. е. записываем с помощью формул алгоритм, по которому можно рассчитать критерий для любого плана.
Составляем формулы ограничений, которые показывают, какие планы имеет смысл рассматривать при выборе оптимального.
Только после составления математической модели имеет смысл вводить информацию в ЭВМ.
Пример
Процесс изготовления двух видов изделий состоит в последовательной обработке каждого из них на трех станках. Возможности использования каждого из них ограничены 10-ю часами в сутки. Удельное время обработки и удельная прибыль для каждого изделия приведены в табл.6.7.2. Найти оптимальный план выпуска каждого изделия.
Таблица 6.7.2
| Изделие | Время обработки одного изделия, мин | Прибыль на одно изделие, $ | ||
| Станок 1 | Станок 2 | Станок 3 | ||
| A | 10 | 6 | 8 | 2 |
| B | 5 | 20 | 15 | 3 |
Составляем модель по предложенному выше плану:
Критерий оптимизации – общая прибыль (ОП), планируемые параметры – число запланированных к выпуску изделий каждого вида (kA,kВ).
Цель оптимизации – максимальная прибыль.
Целевая функция – ОП = kAПА+kBПВ, где ПАи ПВ– удельные прибыли от продажи каждого вида изделий.
Ограничения – в этой задаче наложены ограничения только по времени использования в трудовом процессе каждого станка:
Станок 1: tA1kA+ tB1kB <= 600;
Станок 2: tA2kA+tB2kB <= 600;
Станок 3: tA3kA+ tB3kB <= 600.
Здесь индексы показывают, какому станку и изделию соответствует удельная норма времени обработки. Например, tB2– норма времени обработки одного изделияВна станке 2.
На рис. 6.7.1 изображен пример расположения модели на рабочем листе Excel.
| A | B | C | D | E | F | G | |||
| 1 | Изделие | Время обработки одного изделия, мин | Удельная прибыль | План выпуска изделий | Ожидаемая прибыль | ||||
| 2 | Станок 1 | Станок 2 | Станок 3 | ||||||
| 3 | A | 10 | 6 | 8 | $2 | ||||
| 4 | B | 5 | 20 | 15 | $3 | ||||
| 5 | Время по плану | Общая прибыль | |||||||
| 6 | Допустимое время | 600 | 600 | 600 | |||||
Рис. 6.7.1
В ячейки F3,F4 вводится ориентировочный план. Можно оставить их пустыми. В ячейкиG3,G4 вводятся формулы прибыли по каждому виду изделий, в ячейкеG5 эти прибыли суммируются. В ячейкиB5:D5 вводятся левые части формул ограничений.
После того, как все элементы модели занесены на рабочий лист, можно вызывать команду Сервис Поиск решения… В ее диалоговом окне для нашего примера следует установить такие значения параметров:
"Установить целевую ячейку" – G5 (ячейка, в которой находится окончательное значение целевой функции).
"Равной" – максимальному значению.
"Изменяя ячейки" – F3:F4 (ячейки, в которых находятся планируемые параметры. После окончания работы команды в них будут записаны оптимальные значения).
"Ограничения" – для заполнения этого окна надо нажать кнопку <Добавить>. В появившемся окне Добавление ограничения три поля. В левом указывают адрес ячейки, в которой сосчитана та часть ограничения, которая меняет значение для разных планов. В правом – должна стоять константа, с которой сравнивается значение левого поля при разных планах. Если она уже введена на рабочий лист, здесь можно указать ее адрес. Для нашего примера в левое поле вводим В5, в правое – В6, в центральном поле устанавливаем соотношение <=. Нажимаем кнопку <Добавить>. Повторяем аналогичные действия для ввода ограничений по второму и третьему станкам. После установки последнего ограничения вместо кнопки <Добавить> нажимают <ОК>. Если какие-то ограничения оказались лишними или введены неверно, это можно исправить кнопками<Удалить> и <Изменить>.
Нажимаем кнопку <Параметры>. Появляется диалоговое окно Параметры поиска решения. Здесь оговариваются метод и точность решения. Для задач линейного программирования достаточно установить только параметры "Линейная модель" и "Неотрицательные значения", закрыть окно кнопкой <ОК> и нажать кнопку <Выполнить>.
После окончания расчетов команда выдает окно Результаты поиска решения. Реплика, которая помещена в него, либо подтверждает успешность решения, либо предупреждает, что оптимальное решение не найдено. В этом случае надо проверить, правильно ли составлена и введена модель.
studfiles.net
 )
) )
)