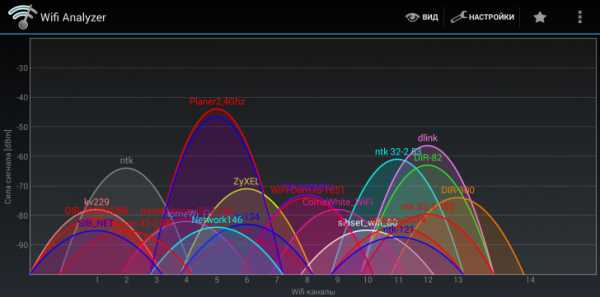
Большая Энциклопедия Нефти и Газа. Стохастическая оптимизация
Алгоритм - стохастическая оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Алгоритм - стохастическая оптимизация
Cтраница 1
Алгоритмы стохастической оптимизации, за исключением градиентных методов, могут быть отнесены к так называемым поисковым методам детерминированной оптимизации. [1]
Все алгоритмы однопараметрической стохастической оптимизации, описанные в § 3.2 и использующиеся в непрямых алгоритмах оптимизации, по своему замыслу могут быть также отнесены к непрямым алгоритмам оптимизации. [2]
К алгоритмам стохастической оптимизации необходимо тем более прибегать при решении задач оптимизации, возникающих при физическом моделировании, при котором, как правило, экспериментальные данные подвержены различного рода искажениям. В этом случае, если исследователь ставит задачу оптимизации некоторого выбранного критерия качества ( математического описания которого нет, но есть возможность получать значения функции в результате натурных обычно трудоемких экспериментов) алгоритмы стохастической оптимизации используются поитерационно. [3]
Рассматриваемые ниже алгоритмы однопараметрической многоэкстремальной стохастической оптимизации не требуют непрерывности f ( x) ( они годны для решения задачи оптимизации гладких функций), что существенно для практических задач, так как исследователь обычно не знает свойств целевой функции построенной математической модели; более того, ему не требуется получения точки экстремума с высокой степенью точности, потому что используемая им математическая модель не является абсолютно адекватной реальной конструкции. [4]
Во всех алгоритмах стохастической оптимизации векторы х - , определяемые из приведенного выше рекуррентного соотношения, также являются случайными, и поэтому для них необходимо рассматривать сходимость в вероятностном смысле. Обычно в методах стохастической оптимизации пользуются тремя видами сходимости: сходимостью по вероятности, сходимостью в среднеквадратичном и сходимостью почти наверное, или с вероятностью единица. [5]
Основными требованиями сходимости алгоритмов стохастической оптимизации являются ограниченность и замкнутость решения целевой функции, требования, накладываемые на асимптотическую скорость изменения шаговых множителей [ см. условия (3.4) ], а также ряд естественных предположений относительно ограниченности влияния случайных помех. [6]
Прежде чем перейти к конкретным алгоритмам, напомним условия, при которых сходятся алгоритмы стохастической оптимизации. Строгий анализ сходимости и скорости сходимости алгоритмов представляет интерес фактически лишь для разработчиков методов оптимизации и выходит за рамки данной книги, поэтому в дальнейшем мы ограничимся лишь кратким их описанием. [7]
Излагаются основы математических методов, используемых при планировании и обработке результатов эксперимента. Рассматриваются вопросы первичной обработки данных, методы прикладной статистики, методы экстремального планирования экспериментов, алгоритмы стохастической оптимизации. [8]
К алгоритмам стохастической оптимизации необходимо тем более прибегать при решении задач оптимизации, возникающих при физическом моделировании, при котором, как правило, экспериментальные данные подвержены различного рода искажениям. В этом случае, если исследователь ставит задачу оптимизации некоторого выбранного критерия качества ( математического описания которого нет, но есть возможность получать значения функции в результате натурных обычно трудоемких экспериментов) алгоритмы стохастической оптимизации используются поитерационно. [9]
В ряде случаев, когда не требуется найти экстремум с высокой степенью точности, данные алгоритмы могут конкурировать с алгоритмами нелинейного программирования. Кроме некоторых алгоритмов случайного поиска, б6 ль-шая часть алгоритмов детерминированной оптимизации малоэффективна при оптимизации в условиях помех. Большинство алгоритмов стохастической оптимизации обладает свойствами сглаживания, а потому может с успехом применяться для решения задач негладкой ( недифференцируемой) детерминированной оптимизации. [10]
Получение коэффициентов функции регрессии производится с помощью МНК. Так как далее МНК будет использоваться неоднократно в алгоритмах стохастической оптимизации, приведем все вычисления, которые производятся данным методом. [11]
Страницы: 1
Стохастическая оптимизация — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Стохастическая оптимизация — класс алгоритмов оптимизации, использующая случайность в процессе поиска оптимума. Случайность может проявляться в разных вещах.
Алгоритмы стохастической оптимизации используются в случае, если целевая функция сложная, многоэкстремальная, с разрывами, с помехами и пр.
Напишите отзыв о статье "Стохастическая оптимизация"
Литература
- [www.math.spbu.ru/user/gran/sb1/SB1.htm Стохастическая оптимизация в информатике] / Под ред. О.Н. Граничина. — СПб: Издательство С.-Петербургского университета, 2005. — Т. 1. — 296 с. — ISBN 5-288-03700-0.
Программное обеспечение
- FortSP — коммерческое ПО (Англия)
- OpenOpt — свободное ПО с коммерческим дополнением для решения задач стохастической оптимизации (Украина)
Отрывок, характеризующий Стохастическая оптимизация
– Я и не желаю. – Без жалованья членом, – повторил Аракчеев. – Имею честь. Эй, зови! Кто еще? – крикнул он, кланяясь князю Андрею.стохастическая оптимизация - это... Что такое стохастическая оптимизация?
стохастическая оптимизация мат. stochastic optimizationБольшой англо-русский и русско-английский словарь. 2001.
- стохастическая определенность
- стохастическая ошибка
Смотреть что такое "стохастическая оптимизация" в других словарях:
Стохастическая оптимизация — Стохастическая оптимизация класс алгоритмов оптимизации, использующая случайность в процессе поиска оптимума. Случайность может проявляться в разных вещах. Алгоритмы стохастической оптимизации используются в случае, если целевая функция… … Википедия
Стохастичность — (др. греч. στόχος цель, предположение) означает случайность. Стохастический процесс это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны,… … Википедия
Ширяев Альберт Николаевич — (р. 1934), математик, член корреспондент РАН (1997). Труды по теории вероятностей и математической статистике. * * * ШИРЯЕВ Альберт Николаевич ШИРЯЕВ Альберт Николаевич (р. 1934), российский математик, член корреспондент РАН (1997). Труды по… … Энциклопедический словарь
Финансовая математика — Финансовая математика раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим… … Википедия
С — Сальдо (balance) Cальдо внешней торговли [balance of trade] Сальдо государственного бюджета [balance of state budget] Сальдо торгового баланса см. Сальдо внешней … Экономико-математический словарь
линейная — 98 линейная [нелинейная] электрическая цепь Электрическая цепь, у которой электрические напряжения и электрические токи или(и) электрические токи и магнитные потокосцепления, или(и) электрические заряды и электрические напряжения связаны друг с… … Словарь-справочник терминов нормативно-технической документации
Программное управление — управление режимом работы объекта по заранее заданной программе (См. Программа). П. у. может осуществляться как с использованием обратной связи (См. Обратная связь), (системы с замкнутой цепью воздействия), так и без неё (системы с… … Большая советская энциклопедия
Равновесие, совершенное по под-играм — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. Равновесие, совершенное по подыграм принцип оптимальности в теории игр, представляющий очищ … Википедия
dic.academic.ru
НПК стохастической оптимизации - Энциклопедия по экономике
Математическая модель задачи стохастической оптимизации календарных планов основного производства НПП, обеспечивающая эффективную детализацию производственной программы предприятия по этапам планового периода, должна включать жесткие вероятностные ограничения, накладываемые на условия ведения технологических процессов и состояния внешних связей и гарантирующие выполнение оптимального текущего плана. Учитывая, что в ходе реализации производственной программы случайные возмущающие воздействия будут порождать [c.59] Рассмотрим особенности постановки и решения задачи стохастической оптимизации производственной программы НПП при параметрических связях элементов [52]. [c.68]Результаты идентификации вероятностных условий задачи стохастической оптимизации календарного планирования основного производства НПП показывают, что случайные параметры модели (3.124) — (3.136) можно считать независимыми друг от друга случайными величинами, подчиняющимися нормальному закону распределения, с соответствующими математическими ожиданиями и дисперсиями [c.88]
В результате решения задачи календарного планирования определяются технико-экономические показатели, обеспечивающие оптимальную реализацию месячной производственной программы НПП с детализацией по декадам или неделям. Результаты расчетов регулярно представляются в плановый отдел предприятия. Как показывает опыт эксплуатации, применение задачи стохастической оптимизации календарного планирования основного производства НПП является важным средством повышения экономической эффективности функционирования предприятия. [c.178]
В сформулированной задаче, как и вообще в задачах финансового планирования, ограничения сверху и снизу, зависят от сценариев. Корректное генерирование выборочных траекторий информационного процесса для данной задачи является решающим фактором надлежащей формулировки задачи стохастической оптимизации. [c.33]
Задачи по оптимизации решаются различными математическими методами, в основе которых лежат теория вероятностей и математическая статистика, линейная алгебра, нелинейное программирование и, в частности, его простейшая форма — квадратичное программирование, а также стохастическое и динамическое программирования и, наконец, матричное исчисление. [c.18]
Традиционные логические приемы обработки информации Приемы детерминированного анализа л Приемы финансовой математики Приемы стохастического анализа Приемы оптимизации показателей Психологические приемы творческого мышления [c.24]
В процессе проведения коэффициентного анализа денежных потоков особое внимание уделяется факторному анализу, т.е. количественному измерению влияния различных объективных и субъективных факторов (причин), оказывающих прямое или косвенное воздействие на изменение рентабельности, эффективности использования денежных средств организации в анализируемом периоде. Факторный анализ (прямой и обратный, детерминированный и стохастический) проводится с использованием различных приемов моделирования факторных систем (расширения, удлинения, сокращения, оптимизации и т.д.). [c.401]
Традиционные способы обработки информации Способы детерминированного факторного анализа Способы стохастического факторного анализа Способы оптимизации показателей [c.39]
Требование реалистичности подхода к учету стохастических свойств некоторых массивов информации в таких широких задачах, какими являются задачи оптимального отраслевого и народнохозяйственного планирования, заставляют вспомнить об аппарате теории надежности, применимом к топологическим схемам сложной структуры. Принадлежащее этой теории понятие резервов дополняют методические средства оптимизации, а сама задача управления надежностью сводится к оптимизационной задаче управления элементной надежностью, резервами и топологической структурой системы. [c.35]
Разнообразны типы математических моделей, используемых на различных уровнях при оптимизации -планирования развития ЕГС линейные, нелинейные, целочисленные, стохастические модели. [c.61]
При оптимизации планирования развития ЕГС стохастические подходы на верхнем уровне не используются. [c.62]
Ниже будет описана модификация локальной постановки задачи оптимизации кратности запасов газа, которая предельно упрощена с точки зрения учета различных распределительных аспектов плана. Учет в основном только адаптивной характеристики надежности плана и соответственно небольшая размерность задачи позволяют поставить и реализовать ее как задачу стохастического программирования. [c.74]
Рассмотрим возможности применения различных постановок одно-этапной задачи стохастического программирования для оптимизации текущей производственной программы НПП. Отличительной особенностью производственной программы является то, что она принимается до наблюдения реализаций случайных параметров условий задачи и не может быть скорректирована по фактически реализованным значениям внешних и внутренних связей. [c.56]
Учитывая указанные обстоятельства, представляется целесообразным использование многоэтапной постановки стохастической задачи оптимизации календарного планирования основного производства НПП с жесткими условными вероятностными ограничениями следующего вида [c.60]
Необходимо отметить, что в ряде случаев предположение о независимости случайных параметров a/ -(w), й,-(со) в задаче Г3.25) для технологических процессов нефтеперерабатывающих предприятий оказывается недостаточно обоснованным. Между элементами матрицы условий и вектора ограничений имеют место функциональные связи и корреляции, учет которых оказывает существенное влияние на вид и свойства стохастической задачи, а также и на конечные результаты оптимизации. [c.68]
Примером связи между элементами различных вектор-столбцов в задаче оптимизации производственной программы НПП может служить параметрическая взаимосвязь варьируемых технологических коэффициентов и качественных характеристик материальных потоков, взаимосвязь коэффициентов отбора и качественных характеристик базовых компонентов, вырабатываемых в процессе разделения и вовлекаемых на смешение в товарном блоке. Следовательно, в рассматриваемом случае в стохастической задаче планирования необходимо учитывать дополнительные условия и ограничения, обеспечивающие согласованность режимов взаимосвязанных технологических звеньев не только по количественным, но и по качественным показателям, учет которых обеспечивает повышение адекватности модели планирования реальным условиям функционирования объекта. [c.70]
Используя декомпозиционный подход, стохастическую задачу оптимизации производственной программы НПП с учетом параметрических связей варьируемых элементов можно сформулировать в виде взаимосвязанно решаемых главной задачи [c.71]
Эти обстоятельства обусловливают необходимость разработки вероятностных динамических постановок и соответствующих стохастических моделей задач оптимизации календарных планов нефтеперерабатывающих производств. [c.78]
Разбивка годовой производственной программы на календарные отрезки времени осуществляется на основе вероятностной модели многоэтапной стохастической задачи оптимизации календарною планирования основного производства НПП. [c.177]
Применение стохастической модели оптимизации календарного планирования основного производства НПП позволяет повысить степень обоснованности и надежности плановых расчетов и снижает вероятность потерь ожидаемой прибыли, возникающих из-за корректировок первоначально принятых плановых заданий. [c.178]
Обоснованы вероятностные постановки задач текущего и календарного планирования производственной программы НПП в условиях неполноты технико-экономической информации, обеспечивающие надежность плановых решений. Многоэтапная стохастическая задача оптимизации отражает адаптивный характер процедур принятия плановых решений и повышает реализуемость производственной программы предприятия. [c.215]
В изучаемой задаче исходные данные имеют стохастическую неопределенность, которая обусловлена объективными обстоятельствами любых технико-экономических задач, а также нестабильностью современной экономики АПК. Это проявляется в том, что для любых исходных данных нельзя определить их точные значения, а можно указать лишь интервал возможных значений. В этом случае результаты оптимизации не являются однозначными и ее ценность резко снижается. [c.165]
На этапе развитого социализма расширяется само понятие эффективности, более полно охватывая факторы общественного производства. Современная наука трактует эффективность как универсальную социально-экономическую категорию, характеризующую объективные причинно-следственные или стохастические связи и соотношения между затратами и результатами, подлежащие планомерному регулированию в целях оптимизации общественного производства на различных его уровнях. Такая трак- [c.12]
Проблема оптимизации поисково-разведочных работ формулируется как детерминированная задача линейного и динамического программирования различной структуры и степени сложности с функционалом в виде минимизации суммарных затрат на прирост запасов или максимизации прироста запасов для заданного лимита капиталовложений. При такой постановке вопроса, на наш взгляд, многие важные аспекты решаемой проблемы оказываются не учтенными. В первую очередь это касается экономической ценности, а также ограниченности ресурсов в недрах. Последнее выражается в затратах обратной связи (рентной оценке) исчерпания возможных открытий. В большинстве предложенных моделей ограничения на суммарный объем извлекаемых запасов в явном виде не отражаются. Далее, рассматриваемые модели обычно линейные и детерминированные, в то время как функция затраты — выпуск в ГРР имеет резко выраженный нелинейный и стохастический характер. Наконец, в моделях не учитывается фактор времени, что недопустимо при изучении столь длительных процессов, как освоение ресурсов нефти и газа. [c.165]
В последние годы значительно увеличилось количество людей, сфера деятельности которых связана с работой на финансовых рынках. Для этих специалистов необходимо хорошее знание основ теории вероятности и математической статистики, так как результаты решения об инвестировании в различные финансовые инструменты (активы) всегда имеют ту или иную степень неопределенности. В этой книге сделана попытка систематизирование рассмотреть практические методы статистики применительно к финансам. Наибольший интерес данная книга может представлять для трейдеров/портфельных менеджеров, то есть специалистов, принимающих самостоятельные решения на финансовых рынках в условиях неопределенности. Изложение материала начинается с базовых понятий, и постепенно переходит к достаточно сложным методам, применяющимся при анализе инвестиционных рисков. В книге содержится большое количество практических алгоритмов вычисления и оптимизации различных финансовых стохастических переменных. [c.10]
Стохастической (вероятностной) моделью называют такую модель, в которой имеется неопределенность, т.е. когда условия (ограничения) задачи или критерий оптимизации (целевая функция) или то и другое являются какой-нибудь числовой характеристикой (например, математическим ожиданием) случайных величин. [c.134]
Часть I 3.3. СТОХАСТИЧЕСКИЙ МЕТОД ПОПАРНОЙ ОПТИМИЗАЦИИ ПОДГРАФОВ [c.148]
Способы детерминированного факторного анализа Способы стохастического факторного анализа Способы оптимизации показателей [c.489]
Как указывалось ранее, на внедрение этого метода на наших предприятиях, руководство которых решит перейти на логистический метод управления, потребуется не менее 10-15 лет из-за отсутствия в настоящее время необходимого логистического окружения и огромных инвестиций, которых сегодня нет у многих наших предприятий. У нас довольно сложные условия снабжения, и они совершенно не похожи на эти закладываемые модели оптимизации запасов транзитные поставки составляют порядка 80%. Многовариантные расчеты, касающиеся, в частности, используемой информации для управления запасами, проводятся на основе детерминированных данных, например, когда точно известен объем поставки или интервал поставки и т.п. В настоящее время на наших предприятиях процесс снабжения сегодня является стохастическим, протекающим с большой неравномерностью транзитных поставок по объемам и интервалам (см. табл. 1.1-1.7). Поэтому на этапе внедрения логистических методов управления, на наш взгляд, нельзя применять вышеуказанные инструменты для расчетов при поиске оптимального варианта. Возможно, этот метод когда-нибудь заработает и у нас. Но сегодня и вряд ли в ближайшей [c.524]
Более широкие возможности имеет пакет Стохастическая оптимизация", созданный на базе ППП Линейное программирование в АСУ" (ППП ЛП АСУ) [102]. ППП ЛП АСУ предназначен для решения и анализа задач линейного программирования (ЛП), нелинейного программирования (НЛП) с нелинейными функциями сепарабельного вида, целочисленного программирования (ЦП) и задач специальной узкоблочной структуры. Размерность решаемых задач составляет для ЛП до 16000 строк, для ЦП — до 4095 целочисленных переменных и 60000 строк для задач узкоблочной структуры. Пакет может быть использован также для решения задач стохастического программирования (СТП) при построчных вероятностных ограничениях. В последнем случае необходимо предварительно построить детерминированный аналог. [c.179]
Базовой идеей всех алгоритмов обучения является учет локального градиента в пространстве конфигураций для выбора траектории быстрейшего спуска по функции ошибки. Функция ошибки, однако, может иметь множество локальных минимумов, представляющих суб-оптимальные решения. Поэтому градиентные методы обычно дополняются элементами стохастической оптимизации, чтобы предотвратить застревание конфигурации сети в таких локальных минимумах. Идеальный метод обучения должен найти глобальный оптимум конфигурации сети4. [c.45]
В финансовой теории возникают и иные оптимизационные задачи, которые в виду "неопределенности окружающей среды" можно отнести (как и в случае, рассмотренном Г. Марковитцем) к проблемам теории стохастической оптимизации. При этом сразу следует отметить, что финансовая проблематика выдвинула целый ряд нетрадиционных, нестандартных оптимизационных задач хеджирования (относительно понятия "хедж" см. 1Ь, гл. V), "нестандартность" которых заключается в том, что оптимальное хеджирование как управление должно обеспечивать выполнение некоторых свойств с вероятностью единица, а не, скажем, в среднем, как это обычно принято в теории стохастической оптимизации. (По поводу задач со среднеквадратичным критерием см. далее Id.) [c.145]
Три концентрических круга на рисунке показывают, хотя и схематично, развитие событий на рассматриваемом поле деятельности, начиная от основания Данцигом, Беллманом, Марковитцем, Мертоном стохастической оптимизации в 1950 гг. и 1960 гг. Далее идут ранние модели Бредли и Крэйна, Чарнеса и его учеников, Зи-ембы и его учеников в 1970 гг. и 1980 гг. Затем имело место значительное продвижение в развитии подобных моделей многими исследователями в 1990 г., чему содействовали новые вычислительные возможности и огромные суммы ресурсов, которыми нужно было [c.27]
Этапы моделирования инвестиционного цикла . построение модели, оценка параметров, практическое применение для принятия решений, оптимизации и прогнозирования. Интерфейсные, фактуальные и процедурные знания. Семантические сети. Синтез модели из типовых модулей. Стохастические сети Петри. Векторные функции денежных потоков в проектировании инвестиционных циклон. Учет факторов риска и неопределенности в моделях инвестиций. [c.75]
Причины появления, логика формирования и перспективы развития этих направлений достаточно очевидны. Во-первых, на уровне хозяйствующего субъекта финансы и бухгалтерский учет тесно переплетены. Вряд ли оспариваем тезис о том, что невозможно стать грамотным финансистом без надлежащего и, заметим, весьма приличного знания концептуальных основ бухгалтерского учета, его логики и техники. Верно и обратное бухгалтер, ограничивающий сферу своей деятельности следованием типовым проводкам, не желающий вникнуть в специфику финансового планирования, бюджетирования и имитационного финансового моделирования, никогда не сможет подняться выше уровня заурядного клерка. Не случайно, в развитых странах, в частности, в странах, исповедующих англо-американскую модель бухгалтерского учета, проводят различие между собственно бухгалтером (a ountant и счетоводом (bookkeeper). Дело в том, что решения финансового характера на уровне предприятия сводятся, по сути (а) к оптимизации его баланса, являющегося, как известно, наилучшей финансовой моделью предприятия, и (б) инициализации и оптимизации денежных потоков. Подобные решения, с одной стороны, базируются на доскональном понимании принципов движения средств по счетам бухгалтерского учета, а, с другой стороны, предполагают применение разнообразных финансовых моделей, учитывающих, в том числе, стохастический характер параметров многих операций и временную ценность де- [c.283]
Для проведения численных расчетов строится четырехблочная модель задачи предварительного этапа, являющаяся детерминированным аналогом вероятностной модели стохастической задачи оптимизации. Эта модель обеспечивает детализацию месячной производственной программы предприятия по цехам, установкам и процессам с разбивкой по неделям. [c.177]
В этой книге сделана попытка систематизированно рассмотреть практические методы статистики применительно к финансам. Наибольший интерес данная книга может представлять для трейдеров/портфельных менеджеров, то есть специалистов, принимающих самостоятельные решения на финансовых рынках в условиях неопределенности, а также для студентов экономических и финансовых вузов. Изложение материала начинается с базовых понятий, и постепенно переходит к достаточно сложным методам, применяющимся при анализе инвестиционных рисков. В книге содержится большое количество практических алгоритмов вычисления и оптимизации различных финансовых стохастических переменных. [c.2]
Разработан ряд стохастических методов решения поставленной оптимизационной задачи распараллеливания вычислений. В первом методе — стохастическом методе попарной оптимизации подграфов — поиск оптимального решения осуществляется за счет взаимного (стохастического) переноса вершин между различными парами подграфов графа алгоритма. Второй метод — метод Монте-Карло случайного блуждания вершин графа алгоритма по подграфам — основан на отождествлении вершин графа алгоритма с некоторыми частицами, совершающими случайные блуждания по областям-подграфам в потенциальном силовом поле, роль потенциала которого играет минимизируемый функционал. Наиболее вероятное состояние подобной системы частиц соответствует минимуму потенциала —-и, следовательно, является искомым решением. Поиск такого состояния осуществляется методом Монте-Карло с использованием специальной процедуры имитации отжига . Третий метод — стохастический метод наискорейшего спуска — основан на использовании дискретного аналога градиента минимизируемого функционала. Все разработанные методы реализованы программно и являются частью системы программ PARALLAX. Проведено тестирование созданных программ и сравнение их работы на простейших примерах. [c.166]
economy-ru.info
стохастическая оптимизация - это... Что такое стохастическая оптимизация?
стохастическая оптимизация adjecon. stochastische Optimierung
Универсальный русско-немецкий словарь. Академик.ру. 2011.
- стохастическая независимость
- стохастическая переменная
Смотреть что такое "стохастическая оптимизация" в других словарях:
Стохастическая оптимизация — Стохастическая оптимизация класс алгоритмов оптимизации, использующая случайность в процессе поиска оптимума. Случайность может проявляться в разных вещах. Алгоритмы стохастической оптимизации используются в случае, если целевая функция… … Википедия
Стохастичность — (др. греч. στόχος цель, предположение) означает случайность. Стохастический процесс это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны,… … Википедия
Ширяев Альберт Николаевич — (р. 1934), математик, член корреспондент РАН (1997). Труды по теории вероятностей и математической статистике. * * * ШИРЯЕВ Альберт Николаевич ШИРЯЕВ Альберт Николаевич (р. 1934), российский математик, член корреспондент РАН (1997). Труды по… … Энциклопедический словарь
Финансовая математика — Финансовая математика раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим… … Википедия
С — Сальдо (balance) Cальдо внешней торговли [balance of trade] Сальдо государственного бюджета [balance of state budget] Сальдо торгового баланса см. Сальдо внешней … Экономико-математический словарь
линейная — 98 линейная [нелинейная] электрическая цепь Электрическая цепь, у которой электрические напряжения и электрические токи или(и) электрические токи и магнитные потокосцепления, или(и) электрические заряды и электрические напряжения связаны друг с… … Словарь-справочник терминов нормативно-технической документации
Программное управление — управление режимом работы объекта по заранее заданной программе (См. Программа). П. у. может осуществляться как с использованием обратной связи (См. Обратная связь), (системы с замкнутой цепью воздействия), так и без неё (системы с… … Большая советская энциклопедия
Равновесие, совершенное по под-играм — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. Равновесие, совершенное по подыграм принцип оптимальности в теории игр, представляющий очищ … Википедия
universal_ru_de.academic.ru
Стохастическая оптимизация — с русского
См. также в других словарях:
Стохастическая оптимизация — Стохастическая оптимизация класс алгоритмов оптимизации, использующая случайность в процессе поиска оптимума. Случайность может проявляться в разных вещах. Алгоритмы стохастической оптимизации используются в случае, если целевая функция… … Википедия
Стохастичность — (др. греч. στόχος цель, предположение) означает случайность. Стохастический процесс это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны,… … Википедия
Ширяев Альберт Николаевич — (р. 1934), математик, член корреспондент РАН (1997). Труды по теории вероятностей и математической статистике. * * * ШИРЯЕВ Альберт Николаевич ШИРЯЕВ Альберт Николаевич (р. 1934), российский математик, член корреспондент РАН (1997). Труды по… … Энциклопедический словарь
Финансовая математика — Финансовая математика раздел прикладной математики, имеющий дело с математическими задачами, связанными с финансовыми расчётами. В финансовой математике любой финансовый инструмент рассматривается с точки зрения генерируемого этим… … Википедия
С — Сальдо (balance) Cальдо внешней торговли [balance of trade] Сальдо государственного бюджета [balance of state budget] Сальдо торгового баланса см. Сальдо внешней … Экономико-математический словарь
линейная — 98 линейная [нелинейная] электрическая цепь Электрическая цепь, у которой электрические напряжения и электрические токи или(и) электрические токи и магнитные потокосцепления, или(и) электрические заряды и электрические напряжения связаны друг с… … Словарь-справочник терминов нормативно-технической документации
Программное управление — управление режимом работы объекта по заранее заданной программе (См. Программа). П. у. может осуществляться как с использованием обратной связи (См. Обратная связь), (системы с замкнутой цепью воздействия), так и без неё (системы с… … Большая советская энциклопедия
Равновесие, совершенное по под-играм — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. Равновесие, совершенное по подыграм принцип оптимальности в теории игр, представляющий очищ … Википедия
translate.academic.ru
Стохастическая онлайн оптимизация в случае тяжелых хвостов стохастических градиентов
Транскрипт
1 Стохастическая онлайн оптимизация в случае тяжелых хвостов стохастических градиентов Гасников А.В. Кафедра МОУ ФУПМ, ПреМоЛаб МФТИ ИОИ-2014, о. Крит (Греция), октябрь,
2 Рассмотрим задачу выпуклой стохастической оптимизации: где f x, выпуклая по п.н. 2 f x E f x, min, xq n x ( n 1) функция. Будем считать, что f x, M ( x и E перестановочны), а размер выпуклого замкнутого множества Q равен R (в действительности, достаточно считать, что R расстояние от точки старта до решения, при этом множество Q может быть не ограничено). Можно предложить такой (SA) метод, на каждом шаге (итерации) которого f x, считается проекция стохастического (суб-)градиента функции (с независимой разыгранной с.в. ) по x на множество Q, что ( 0 малый доверительный уровень) 2
3 1 1 ln P x E f x, min, N N E f x CMR xq, N где C константа ( 10), а с.в. x N то, что выдает алгоритм после итераций. Таким образом, для достижения точности по функции и доверительного уровня методу потребуется ln MR итераций (вычислений стохастического градиента и его проектирований). Можно показать, что если использовать метод Монте-Карло (SAA), заключающийся в замене исходной задачи следующей задачей 1 N N k1 f x, k min, xq 3
4 где с.в. k i.i.d., и распределены также как и, то для того, чтобы гарантировать, что абсолютно точное решение этой новой задачи является, -решением исходной задачи потребуется порядка ln M R nln MR итераций. Приведенный факт хорошо поясняет, что подход, связанный с усреднением случайности за счет самого метода более предпочтителен, чем замена задачи ее стохастической аппроксимацией (эта идея довольно стара; по-видимому, одним из первых кто количественно смог это прочувствовать был Б.Т. Поляк). Более предпочтителен не только тем, что допускает адаптивность постановки и легко переносится на онлайн модификации исходной задачи, но, прежде всего, лучшей приспособленностью к большим размерностям. Подробнее о методах SA написано в статье Juditsky A., 4
5 Lan G., Nemirovski A., Shapiro A. Stochastic approximation approach to stochastic programming // SIAM Journal on Optimization V P О методах SAA написано в монографии Shapiro A., Dentcheva D., Ruszczynski A. Lecture on stochastic programming. Modeling and theory. MPS-SIAM series on Optimization, Здесь важно отметить, что в этой задаче сидит фундаментальная идея о том, что для получения (агрегирования) хороших оценок неизвестных параметров (особенно когда размерность пространства параметров велика) имеет смысл рассматривать задачу поиска оптимальных значений параметра, как задачу стохастической оптимизации и рассматривать выборку, как источник стохастических градиентов. Например, истинное значение неизвестного вектора параметров в предположении верности исходной параметрической гипотезы может быть записано как решение задачи стохастической оптимизации 5
6 * arg max EL, Q (метод наибольшего правдоподобия Фишера), где L, логарифм функции правдоподобия. Однако решать эту задачу обычными методами мы не можем, потому что математическое L, ожидание берется по с.в., распределение которой задается *, а не известно. Этот порочный круг распутывается, если мы будем решать задачу E L, min Q методами стохастической оптимизации, получая на каждом шаге новую реализацию (элемент выборки) и рассчитывая значения градиента L. То, что выдает алгоритм и будет,, k k - 6
7 оценкой вектора неизвестных параметров. Отметим, что, как правило, L, гладкая и -сильно вогнутая дополнительно известно, что (равномерно по ) функция по. Последнее обстоятельство позволяет получить лучшую скорость сходимости по функции M 2 ln ln N N, т.е. (x, f L) Px E f x, min, N N E f x CM 2 xq. ln ln N N Из неравенства Рао Крамера будет следовать, что такая оценка не ln ln N ). Правда, тут улучшаема (с точностью до фактора возникают некоторые тонкости, когда мы говорим о неулучшаемости оценок с учетом вероятностей больших отклонений. Строго говоря, результаты типа Рао Крамера, Ван-Трисса и т.п. (см., например, 7
8 классическую монографию Ибрагимов Хасьминский) позволяют лишь говорить о неулучшаемости в смысле сходимости полных математических ожиданий (без вероятностей больших отклонений), и именно в таком смысле можно получить неулучшаемую (с точностью до мультипликативной константы) оценку: 2, N min, CM E f x E f x xq. N когда f x, Можно обобщить рассмотренную задачу на случай, 2 имеет субгауссовский хвост. Тогда (в том числе в сильно выпуклом случае) вместо 1 ln 2 стоит писать 1, 2 2 f x имеет степенной хвост ln. Если же 8
9 то ( 2) P 2 2 f x, 1 t, 2 M t N 1 N Px E f x, min, N N E f x C MR xq. N Если дополнительно f x E f x, функция, то ( 1) Px E f x E f x C M N -сильно выпуклая 1 N ln ln 2 N, min, xq N. 9
10 Если ничего не известно о f x, 2, кроме 2 2 E f x, M 2 2, то по неравенству Маркова (второе неравенство подразумевает -сильную выпуклость f x ) CMR Px E f x, min, N N E f x xq, N 2 CM Px E f x, min, N N E f x xq. N Все сказанное выше обобщается и на другие прокс-структуры (не обязательно евклидовы). Так в задачах 8, 9 рассматривается проксструктура, порожденная расстоянием KL Кульбака Лейблера (сильно выпуклом в 1-норме с константой 1 на единичном симплексе неравенство Пинскера), по-видимому, наилучшим образом 10
11 подходящая для симплекса (с некоторыми оговорками). Выгода от ее f x, M, что в типичных использования в том, что теперь ситуациях (см. задачу на теорему Б.С. Кашина о поперечниках) дает оценку константы M в n раз лучше, а плата за это увеличение оценки размера области в ln n. Детали имеются в упомянутой в начале замечания статье. Подчеркнем, что все приведенные здесь оценки, вообще говоря (без дополнительных предположений), неулучшаемы (с точностью до мультипликативных констант). Один пример того, как это можно показать был рассмотрен выше (в общем случае следует смотреть монографию Немировского Юдина). Сейчас же отметим, что если f x, гладкая по x функция, с дополнительно известно, что константой Липшица градиента L и(или) сильно выпуклая с 11
12 константой, а вычисление и проектирование стохастического градиента на каждом шаге находится с неконтролируемой точностью, вообще говоря, не случайной природы (в этом месте есть неаккуратность, в действительности, определение -оракула, выдающего стохастический градиент, более тонкое 1 ), то из недавних результатов Nesterov Devolder Glineur и Ghadimi Lan можно получить такие оценки скорости сходимости (здесь стоит отметить большую работу, проделанную П.Е. Двуреченским, по получению нужного обобщения упомянутых выше результатов) -оракул выдает такие F x,, Gx, 1, L для любых x, y Q, что, D G x D, и L 2 0 E f y, E F x, E Gx,, y x y x. 2 12
13 1 p1 2 2 LR DR p p p1 2 D L min N, LR exp NC, p N N L N где 1 f x,, а параметр C некоторая константа, D дисперсия 1,2 p подбирается оптимально исходя из масштаба шума. Дисперсию можно уменьшать, запрашивая на одном шаге реализацию стохастического градиента не один раз, а m раз, и заменяя стохастический градиент средним арифметическим, мы уменьшаем дисперсию в m раз. Это имеет смысл делать, если слагаемое, отвечающее стохастичности, доминирует. Важно, что мы при этом не p 1 увеличиваем число итераций, и слагаемое N остается прежним. Выписанные оценки характеризуют скорость сходимости в среднем. Они с одной стороны не улучшаемы (причем это остается верно при 2 0 и(или) D 0; при D 0 мы считаем n, в противном случае 13
14 оценки улучшаемы методы эллипсоидов и внутренней точки, с n ln R, 1) с точностью до оценками числа итераций типа мультипликативной константы, с другой стороны достигаются. В терминах больших отклонений возникает аналогичные оговорки тем, которые мы выше делали с одним исключением в сильно выпуклом случае появляется дополнительная зависимость от N в множители, содержащем (см. выше). Эти результаты переносятся и на проксструктуры отличные от евклидовой. При этом рассмотрение какойлибо отличной от евклидовой структуры в сильно выпуклом случае (когда минимум достигается на втором выражении), как правило, не имеет смысла, поскольку квадрат евклидовой асферичности p-нормы, возникающий в оценках числа обусловленности прокс-функции в p- норме (это число, в свою очередь, оценивает увеличение числа итераций метода при переходе от евклидовой норме к p-норме), 14
15 больше либо равен 1. Равенство достигается на евклидовой норме. Скажем, для 1-нормы эта асферичность оценивается снизу размерностью пространства. Множество Q должно быть достаточно простой структуры, чтобы на него можно было эффективно проектироваться. Однако в приложениях часто возникают задачи условной минимизации, в которых есть ограничения вида gx 0, где g x выпуклые функции. Зашивать эти ограничения в Q, как правило, не представляется возможным в виду вышесказанного требования. Тем не менее, на основе описанного выше можно строить (за дополнительную логарифмическую плату) двухуровневые методы условной оптимизации подобно тем методам, которые описаны в конце главы 2 и 3 монографии Нестеров Ю.Е. Методы выпуклой оптимизации. М.: МЦНМО, При этом на каждом шаге такого 15
16 метода потребуется проектироваться на пересечение множества Q с некоторым полиэдром, вообще говоря, зависящим от номера шага. Все сказанное выше переносится в полной мере на задачи композитной оптимизации (Ю.Е. Нестеров) и частично на монотонные вариационные неравенства (Ю.Е. Нестеров). Отметим также, что параметры R и могут быть не известны априорно или процедуры их оценивания приводят к слишком соответственно завышенным и заниженным результатам. Это может быть проблемой, поскольку знание этих и других параметров требуется методу для расчета величин шагов. Из этой ситуации можно выйти за логарифмическое (по этим параметрам) число рестартов метода. Стартуя, скажем, с и делая, предписанное этим R число шагов, мы проверяем выполняется ли условие -близости. Если нет, то полагаем R: 2R и т.д. Это константное время и не отразится на 16
17 общих трудозатратах. Аналогичное можно сказать про L и D. Однако если убрать стохастичность, тогда L можно не только эффективнее адаптивно подбирать по ходу самих итераций (увеличив в среднем число итераций не более чем в 4 раза), но и в некотором смысле оптимально самонастраиваться на гладкость функционала на текущем участке пребывания метода (речь идет о недавно предложенном универсальном методе Ю.Е. Нестерова). Для оценки D в ряде случаев бывает эффективнее воспользоваться какой-нибудь статистической процедурой. В число итераций описанных методов не входит размерность пространства n. Это наталкивает на мысль о возможности использовать эти методы, например, в гильбертовых пространствах. Оказывается, это, действительно, можно делать. В частности, концепция неточного оракула позволяет привнести сюда элемент 17
18 новизны, существенно мотивированной практическими нуждами (много материала о градиентных методах решения задач оптимизации в гильбертовых пространствах собрано во втором томе учебника Ф.П. Васильева по методам оптимизации). Наконец, полезно иметь в виду, что за счет допускаемой неточности оракула, выдающего (стохастический) (суб-)градиент, можно погрузить задачу с гельдеровым градиентом,, * f x f y L x y (в том числе и негладкую задачу с ограниченной нормой разности субградиентов 0) в класс гладких задач с оракулом, характеризующимся точностью и 18
19 L 1 L L 2 1 В стохастической онлайн ситуации оценки будут такими: M R M 2 ln N min, N N. Эти оценки достигаются и неулучшаемы. Как видно из этих оценок наличие гладкости ничего не дает. Все что ранее говорилось про прокс-структуру и большие отклонения полностью и практически без изменений (в -сильно выпуклом случае в оценках вероятностей больших уклонений lnln N. ln N) переносится и на онлайн случай. Отметим также, что онлайн методы, как правило, допускают 19
20 прямо-двойственную модификацию (с теми же оценками скорости сходимости) при применении к задачам условной оптимизации. В заключение отметим, что следует различать задачи стохастической оптимизации и задачи, в которые мы сами искусственно привносим случайность (рандомизацию) с целью более эффективного решения задачи. К этой ситуации, скажем, можно отнести случай, когда (негладкий) выпуклый функционал в задаче детерминированный, но представляет собой трудно вычислимый интеграл от параметров, который компактно представим в виде математического ожидания по некоторой не сложной вероятностной мере. Тогда выгоднее считать стохастический градиент. Существенно экономя на вычислениях на каждом шаге и лишь не много теряя на логарифмическом увеличении числа шагов. Такой пример будет рассмотрен в следующей задаче. Однако если мы можем вычислять 20
21 значение функции в детерминированной задаче, в которую мы решали рандомизированным методом, то ни о каких тяжелых хвостах можно не заботиться. Поскольку, выбрав число шагов так, чтобы метод находил -решение с вероятностью 12 и запустив реализаций log плату такого метода мы за дополнительную 1 2 (мультипликативную) получим с вероятностью 1 среди выданных ответов хотя бы одно -решение. Однако предположение о возможности вычислять значения функции в ряде задач натыкается на существенные вычислительные сложности (значительно большие, чем при расчете стохастического градиента). Таким примером T является задача поиска вектора PageRank P p p (P стохастическая матрица), сводящаяся к негладкой задаче выпуклой оптимизации (матричной игре) T max u, P p p min. Кроме того, если us n 1 ps n 1 21
22 рандомизация осуществляется каким-то специальным образом, например, таким, что 2 2 E f x, C * n f x малый добавок * и в точке минимума f x, то приведенные выше оценки можно существенно улучшить (Б.Т. Поляк). Такая рандомизация возникает, например, в связи с изучением безградиентных методов. 22
docplayer.ru