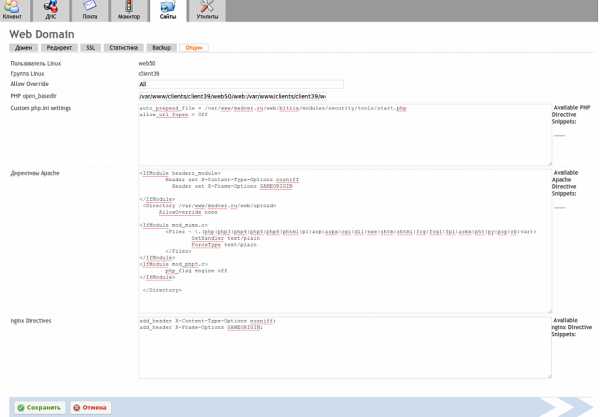
Практическая работа 6 решениЕ задач оптимизации Цель работы. Решение задач оптимизации
Решение задач оптимизации с использованием MS Excel
Решение задач оптимизации с использованием MS Excel
С помощью инструмента «Поиск решения» решаются задачи оптимизации следующих типов.
1. Имеется функция одной или нескольких переменных и необходимо найти значения переменных, при которых функция равна либо минимуму или максимуму.
2. Имеется функция одной или нескольких переменных и необходимо найти значения переменных, при которых функция равна либо минимуму либо максимуму с учётом дополнительных ограничений.
Функция, значение которой отыскивается с помощью инструмента «Поиск решения» называется целевой функцией, а ячейка, где содержится формула для вычисления значений функции, называется целевой ячейкой.
Ограничение состоит из левой части, в которой содержится формула для вычисления некоторой величины, и правой части, в которой указывается величина ограничения. Левая и правая части соединяются либо знаком равенства, либо знаком неравенства.
Пример 1. Надо найти максимум функции при следующих ограничениях:
Эти данные можно внести на лист следующим образом:
| А | В | |
| 1 | Переменные | |
| 2 | Х1 | Х2 |
| 3 | 0 | 0 |
| 4 | Целевая функция | |
| 5 | =300*А3+200*В3 | |
| 6 | Ограничения | |
| 7 | =А3+2*В3 | 10 |
| 8 | =2*А3+В3 | 8 |
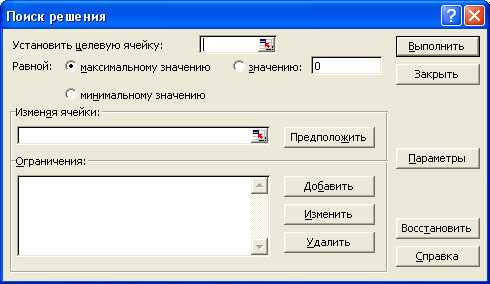
После внесения исходных данных надо сделать активной целевую ячейку и вызвать «Поиск решения» через меню «Сервис\Поиск решения».
В появившемся диалоговом окне надо заполнить ряд полей.
Поле «Установить целевую ячейку» должно содержать адрес целевой ячейки. В нашем случае это адрес А5.
Затем установить переключатель «Равной» в положение «Максимальному значению».
Поле «Изменяя ячейки» должно содержать диапазон ячеек, содержащих независимые переменные. В нашем случае это А3:В3.
Поле «Ограничения» должно содержать все ограничения, если они имеются. В нашем случае, по условию задачи имеются четыре ограничения. Чтобы внести в это поле ограничения надо щелкнуть по кнопке «Добавить».
Появится диалоговое окно с тремя полями расположенными в ряд. Самое левое поле «Ссылка на ячейку», среднее поле со списком, и правое поле «Ограничение».
Поле «Ссылка на ячейку» должно содержать адрес ячейки с формулой ограничения. В поле со списком выбирается знак ограничения. Поле «Ограничение» содержит либо величину ограничения, либо адрес ячейки, где эта величина содержится.
В нашем случае, формула первого ограничения представляет собой просто переменную х1, поэтому указываем адрес А3, затем выбираем из списка неравенство больше или равно и величину ограничения указываем равной нулю. Чтобы добавить следующее ограничение надо в этом же окне щелкнуть по кнопке «Добавить» и внести новые данные. И так, до тех пор, пока не будут набраны данные по всем ограничениям. После внесения данных по последнему ограничению надо щелкнуть по кнопке ОК.
После этого можно щелкнуть по кнопке «Выполнить».
Через некоторое время появиться окно с результатом поиска решения. Возможны два варианта.
Если в окне будет сообщение «Решение найдено», то можно нажимать на кнопку ОК и в ячейках на листе будут содержаться найденные значения.
В нашем случае ячейки должны содержать: А3=2, В3=4, А5=1400, А8=10, А9=8.
Если появится сообщение «Процесс не сходится», то это означает, что решения не существует или оно не найдено при установленных параметрах поиска. Эти параметры можно изменить, если до щелчка по кнопке «Выполнить» нажать кнопку «Параметры». Можно попробовать изменить параметры «Максимальное время», «Предельное число итераций», «относительная погрешность» и «Допустимое отклонение».
Пример 2.
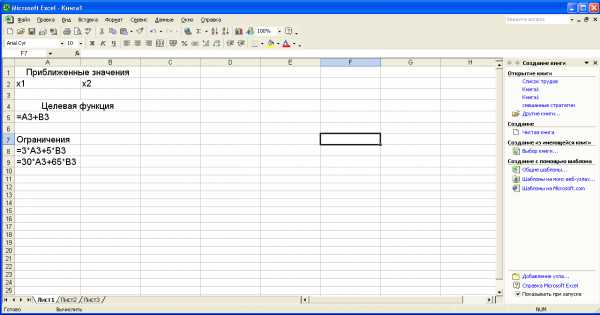
Авиакомпания М* по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно.
Эксплуатация 1 самолета первого типа обойдется 5000$, а второго 9000$. Сколько надо использовать самолетов каждого типа, если для формирования экипажей имеется не более 60 человек.
Для начала, обозначим переменные: пусть X1 – это оптимальное количество самолетов первого типа, X2 – оптимальное количества самолетов второго типа. Очевидно, что стоимость эксплуатации самолетов должна быть минимальной. Следовательно,
5000X1 + 9000X2→min
Теперь определим ограничения. Для формирования экипажей имеется не более 60 человек, следовательно:
3X1+5X2<=60
Пассажиров надо перевезти не менее 700человек, следовательно:
30X1+65X2>=700
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне:
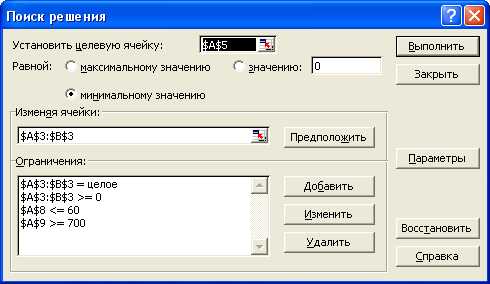
После выполнения поставленной задачи получаем следующие значения переменных. Как показано на рисунке
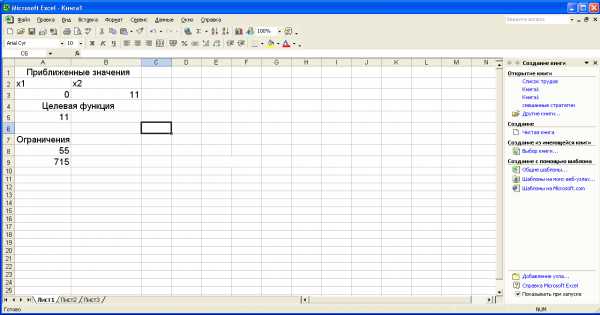
Т.е. нам необходимо (X1=0) 0 самолётов первого класса и (X2=11) 11 самолётов второго класса, для перевозки пассажиров.
studfiles.net
Решение дискретных задач оптимизации
В общем случае дискретный управляемый процесс можно определить как последовательность взаимосвязанных совокупностей элементов, которые можно условно обозначить вектором и на которые можно разбить процесс во времени или пространстве. Составляющими вектора являются элементы совокупности. Каждая совокупность элементов характеризует со стояние процесса, причем каждое последующее состояние зависит только от предыдущего и управления в этот момент . Индекс служит для нумерации состояния и может трактоваться как дискретное время или как дискретная пространственная координата (или позиция). Рассмотрим управляемые дискретные процессы, последовательность состояний которых задается уравнением связи
(3.1)
Обозначим начальное и конечное состояние процесса соответственно и . Постановка задачи оптимизации имеет следующий вид: необходимо определить последовательность управлений которая обеспечит за шагов перевод объекта управления из со стояния в состояние и минимизирует критерий оптимизации . При этом предполагается, что управляющие воздействия должны быть выбраны из допустимой области и промежуточные состояния процесса удовлетворяют ограничению . В связи с тем, что процесс многошаговый критерий оптимизации вычисляется через сумму составляющих на каждом шаге:
(3.2)
Математическая постановка задачи:
определить
На основании выражения (3.2) можно утверждать, что величина критерия оптимизации в конечном итоге зависит только от начального состояния и искомой стратегии:
В связи с этим задачу оптимизации дискретной системы можно сформулировать как задачу на экстремум функции переменных при ограничениях на управление и состояние системы. Эта задача становится трудоемкой, когда - велико, и главное - ограничения на и в дискретных задачах, как правило, имеют такой вид, что задача не решаема методами математического анализа. Однако на практике в производстве и жизненных ситуациях, дискретные задачи оптимизации встречаются очень часто. Основным и очень древним способом решения таких задач является метод перебора. При малой размерности ( и - невелико) и жестких ограничениях на величину составляющих вектора и число допустимых состояний процесса на каждом шаге этот метод позволяет достаточно быстро определить оптимальную стратегию. Однако при увеличении размерности число возможных вариантов становится астрономически большим и их сравнение требует много времени и денежных средств.
Метод динамического программирования во многих случаях позволяет существенно сократить все затраты и определить многошаговую оптимальную стратегию. Оказывается, задачу на экстремум функции переменных можно свести к менее сложных задач на
экстремум функции одной переменной . Идея решения вытекает из принципа оптимальности. Вся траектория движения объекта разбивается на участков (рис. 3.2). Вначале рассматривается один последний участок с номером , и для этого участка определяется оптимальное управляющее воздействие ,которое действует в момент времени и переводит объект из состояния в состояние . Таким образом, решается задача оптимизации с одним неизвестным :
(3.4)
Обозначим минимальное значение критерия оптимизации на этом шаге тогда
(3.5)
Затем рассматриваются два последних участка траектории с номерами и . Считается, что оптимальное управление и соответствующее ему значение критерия на последнем участке известно, тогда минимальное значение критерия оптимизации на двух участках можно представить:
(3.6)
Из выражения (3.6) следует, что при оптимизации критерия на двух участках решается задача с одним переменным , т.е.:
(3.7)
При рассмотрении трех последних участков минимальное значение критерия оптимизации равно:
(3.8)
Для определения необходимо найти оптимальное управление в момент времени , т.е. на третьем от конца траектории участка. По аналогии минимальное значение критерия на всей траектории ( участков)
(3.9)
Таким образом, для определения оптимальных управлений необходимо решить задач оптимизации с одним неизвестным, что можно записать в виде системы функциональных уравнений Беллмана в рекуррентной форме.
…………………………………………………………………………… (3.10)
Из представленной системы уравнений (3.10) видно, что минимальное значение критерия является функцией состояния объекта, в котором он находился в начале оптимизируемого участка . Поскольку при решении всей за дачи оптимизации оптимальная траектория неизвестна, неизвестны и точки . В связи с этим практическая реализация идеи, выраженной в системе (3.10), имеет следующий вид.
Определяется оптимальное управление для всех возможных состояний объекта на каждом шаге, и для всех возможных состояний для оптимального управления вычисляется значение критерия оптимизации, которое становится весовой характеристикой данного состояния. При движении с конца траектории значение критерия в последующих состояниях определяется как минимальная сумма значения критерия предыдущего состояния и приращения критерия в течение одного шага под действием одного из допустимых управлений. Таким образом, значение критерия оптимизации в начальной точке траектории оценивает траекторию в целом. Как следует из сказанного, решение задачи требует вычислительной работы во всем пространстве допустимого рас положения оптимальной траектории. Совершенно очевидно, что чем жестче ограничения на состояние объекта, тем этих вычислений меньше и решение задачи проще. (В классических методах оптимизации имеет место обратная картина.) Как показывает практика, при большом объеме пространства состояний метод динамического программирования дает обязательный выигрыш по сравнению с методом перебора. Описанную выше вычислительную процедуру метода динамического программирования рассмотрим на примере абстрактного процесса, относительно которого известно (рис.31) начальное состояние в момент времени длительность протекания Т интервал дискретизации число шагов дискретизации число возможных состояний - по три на каждом шаге, в том числе и при . Допустимые управления позволяют переход из каждого состояния в момент в каждое состояние в момент как и показано на рис.3.5.
Требуется определить оптимальную траекторию, на которой критерий оптимизации принимает минимальное значение:
(1.П)
где - индекс состояния системы, через который пройдет оптимальная траектория, - индекс временного шага.
Так как при допустимых состояний два, согласно принципу Беллмана решение начинается с момента времени . По заданному правилу (аналитическому выражению) вычисляется значение критерия для всех допустимых состояний процесса в момент времени т.е. значения . Из каждого допустимого состояния временного слоя можно перейти в каждое допустимое состояние временного слоя : для каждого состояния для можно определить три значения критерия соответствующих двум переходам. Затем из них определяется переход с минимальным значением критерия. Этот переход отмечается(запоминается) и это состояние оценивается этим значением критерия. Для примера на рис.3 оптимальные переходы помечены жирной линией. Следовательно, в общем случае величина определяет минимальную стоимость перехода из всех возможных состояний времени в состояние
(2.П)
Например, для рассматриваемой задачи, для узла с индексом значение стоимости перехода в этот узел:
для узла с индексом :
При этом стоимость перехода в общем случае когда критерий зависит от "пути" перехода определяется
(3.П)
где второе слагаемое оценивает стоимость "пути" в состояние из точки . Двигаясь с конца траектории к началу, рассчитываются значения для всех узлов сетки возможных состояний. При этом важно помнить, что значение критерия в узлах сетки последующего числа определяется как сумма критерия предыдущего состояния и плюс оценка состояния в узле рассматриваемого шага. Поэтому минимальное значение критерия за все время движения (четыре шага) и указывает оптимальную траекторию, стоимость которой соответствуй этому критерию. Объем вычислений, которые необходимо выполнить, чтобы решить задачу методом динамического программирования значительно меньше объема вычислений, необходимых при решении задач оптимизации ДМШ методом перебора. Упрощенно это можно объяснить тем, что на каждом шаге для каждой допустимой точки состояния системы проводится отбор неслучайного перехода (согласно критерию) и исключения из дальнейших вычислений остальных переходов.
infopedia.su
Практическая работа 6 решениЕ задач оптимизации Цель работы
Получить общие представления о задачах оптимизации, освоить основные приемы и сервисные надстройки табличных процессоров для оптимизации решений и анализа данных, овладеть практическими знаниями и навыками поиска оптимальных решений в электронных таблицах, решить типовые задачи оптимизации с помощью инструментов табличных процессоров.
Теоретическое введение
В электронных таблицах (ЭТ), помимо базовых операций с данными, можно также эффективно обрабатывать и исследовать результаты, то есть решать задачи оптимизации и анализа решений.
Оптимизационными называются задачи, в которых при заданном множестве вариантов значений исходных параметров, изменяющихся во времени, определяется оптимальный вариант по какому-либо критерию (критериям). Применительно к экономическим явлениям оптимизационными задачами называются ситуации поиска значений, оптимальных для определенных выходных характеристик моделей, которые описывают исследуемые экономические явления. Классическими моделями оптимизации с одним критерием оптимальности являются задачи максимизации общей прибыли предприятия или минимизации общих затрат на производство.
В табличном процессоре MS Excel используют два способа оптимизации и анализа данных:
решение экономических задач типа "что надо, чтобы" методом "Подбор параметра";
анализ экономических решений по типу "что будет, если" с помощью технологии "Поиск решения".
Оптимизация данных методом "Подбор параметра" применяется, как правило, для решения задач, в которых исследуется выходное значение, наиболее значимое для нас (целевая функция), за счет изменения определенного параметра. В этом случае на изменяемый параметр не вводятся ограничения, а величина оптимального значения устанавливается постановщиком задачи. Таким способом можно, например, "улучшить" прибыль до желаемого фиксированного значения за счет изменения объема выпуска или цены продажи до неограниченной величины. Как следствие, оптимизация по технологии "Подбор параметра" ограничена и далека от реальности.
Оптимизация типа "Поиск решения" проводится методом "от обратного". В этом случае для изменяемых параметров можно устанавливать границы (ограничения), в которых они могут изменяться или представляют экономический интерес, при этом поиск оптимального решения ведется либо по критериям экстремальности (минимума и максимума), либо по точному значению, задаваемому постановщиком. К оптимизации "Поиск решения" можно свести многие типовые задачи линейного программирования, например, поиск оптимального состава сырья или составления оптимальных планов производства при ограниченных ресурсах и др. Оптимизация методом "Поиск решений" в отличие от оптимизации методом "Подбор параметра" многовариантна, более гибкая по структуре и достовернее приближает модель к действительности.
Практическая часть Постановка задачи
Требуется оптимизировать различными способами значение общей прибыли, полученной в предыдущей работе (см. таблицу 5), до установленного значения (200000р.)
Таблица 5 – Исходные данные задачи «Оптимизация прибыли»
| Наименование | Выпуск, шт. | Всего | Цена | Выручка | Прибыль | ||
| Январь | Февраль | Март | |||||
| Изделие 9/001 | 700 | 650 | 666 | 2016 | 299,00р. | 602 784,00р. | 120 556,80р. |
| Изделие 9/002 | 310 | 217 | 222 | 749 | 199,00р. | 149 051,00р. | 29 810,20р. |
| Изделие 9/003 | 122 | 129 | 156 | 407 | 150,00р. | 61 050,00р. | 12 210,00р. |
| Прибыль итого | 162 577,00р. | ||||||
studfiles.net
Решение задач оптимизации управления с помощью MS Excel 2010 - Лекции
Цель лекции: Показать возможность графического решения задач с двумя неизвестными.Содержание
- Задача 1.1. Выпуск продукции
- Задача 1.2. Приготовление смесей
- Задача 1.3. Нелинейная задача
- Ключевые термины
- Краткие итоги
- Упражнения
- Задача 1.4
- Задача 1.5
- Линейное программирование: нахождение экстремального значения линейной функции многих переменных при наличии линейных ограничений, связывающих эти переменные.
- Нелинейное программирование:целевая функция и ограничения могут быть нелинейными функциями.
- Целочисленное программирование: особый случай в задачах линейного и нелинейного программирования, когда на оптимальные решения накладывается условие целочисленности искомых параметров.
- Динамическое программирование: для отыскания оптимального решения планируемая операция разбивается на ряд шагов (этапов) и планирование осуществляется последовательно от этапа к этапу. Однако выбор метода решения на каждом этапе производится с учетом интересов операции в целом.
- Теория графов, с помощью которой решаются многие сетевые задачи, связанные с минимальным протяжением сети, построение кольцевого маршрута и т.д.
- набор констант, характеризующих, например, наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы;
- искомые переменные величины, например, количество запланированной к выпуску продукции по всему ассортименту;
- максимум или минимум целевой функции, например, запланированной прибыли;
- систему ограничений в форме линейных уравнений и неравенств, например, условие того, что расход материала не должен превышать его запас;
- требование неотрицательности переменных (если не предусмотрено иное).
Рис. 1.1. Схема моделирования объекта (процесса)
При решении "стандартной" задачи в линейном программировании нужно определить максимум линейной целевой функции
при условиях
Здесь целевая функция формируется как скалярное произведение двух векторов. Один из них — вектор искомых переменных . Компонентами другого вектора являются целевые коэффициенты . Условия задачи можно сформулировать так: "Расход не должен превышать имеющиеся ресурсы ". Вектор расхода есть сумма произведений матрицы нормированных коэффициентов на вектор искомых переменных .
Основной аналитический метод решения задач линейного программирования — это симплексный метод . Он сводится к вычислительной процедуре, основанной на принципе последовательного улучшения решений — перехода от одной базисной точки к другой, для которой значение целевой функции больше. Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов. Геометрическая интерпретация метода состоит в последовательном движении по вершинам симплекса (n-мерного тетраэдра). Симплекс-метод послужил исходным пунктом для разработки целого семейства алгоритмов решения как линейных, так и нелинейных выпуклых задач оптимизации.
Задача 1.1. Выпуск продукции
Фирма производит две модели и сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели требуется досок, а для модели — . Фирма может получать от своих поставщиков до досок в неделю. Для каждого изделия модели требуется 12 мин. машинного времени, а для изделия модели — 30 мин. В неделю можно использовать 160 часов машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели приносит 200 руб. прибыли, а каждое изделие модели — 400 руб. прибыли?
В данном случае объектом является фирма, а ее деятельность представляется в виде математической модели, т.е. учитываются только некоторые количественные стороны этой деятельности. Менеджер (субъект) ставит себе задачу: составить недельный производственный план фирмы. При этом он руководствуется целью моделирования — максимальной эффективностью производства, получением максимальной прибыли.
Построение математической модели
Пусть - количество выпущенных за неделю полок модели , а — количество выпущенных за неделю полок модели . Тогда составим следующие соотношения:
- количество досок, требуемых на неделю для изготовления полок модели .
- количество досок, требуемых на неделю для изготовления полок модели .
- количество досок требуемых на неделю для изготовления книжных полок двух моделей. По условию задачи это число не должно превышать , следовательно, получаем первое ограничение:
| (1) |
12 мин. составляют 0,2 часа, а 30 мин. — 0,5 часа, таким образом:
- количество времени, требуемое на неделю для обработки полок модели ;
- количество времени, требуемое на неделю для обработки полок модели ;
- количество времени, требуемое на неделю для обработки двух моделей. По условию задачи это число не должно превышать 160 часов, следовательно, получаем второе ограничение:
| (2) |
| (2) |
| (3) |
- еженедельная прибыль, получаемая от продажи полок модели .
- еженедельная прибыль, получаемая от продажи полок модели .
- еженедельная прибыль, которая должна быть максимальной.
Таким образом, имеем следующую математическую модель для данной задачи:
;
;
Необходимо найти значения переменных и , при которых данная функция принимает максимальное значение, при соблюдении ограничений, накладываемых на эти переменные.
Решения, удовлетворяющие системе ограничений и требованию неотрицательности, являются допустимыми, а решения, удовлетворяющие одновременно и требованию максимизации (минимизации) целевой функции являются оптимальными.
Область допустимых решений целевой функции можно найти графическим методом.
Построим прямоугольную систему координат, где по оси отложим значения , а по оси отложим значения . Так как, согласно условию (3), и неотрицательны, то можно ограничиться рассмотрением первого квадранта (рисунок 1.2).
Рассмотрим первое ограничение:
Заменим в данном ограничении знак неравенства знаком равенства и построим прямую
Для этого найдем две точки, принадлежащие данной прямой. Пусть, например, , или . — координаты первой точки, принадлежащей прямой.
Пусть , то , следовательно, . — координаты второй точки, принадлежащей прямой. Отметим эти точки на числовых осях.
Аналогично, для второго ограничения:
При ,
При ,
Построим данные прямые (на рисунке они соответственно обозначены (1) и (2))
Теперь найдем на чертеже такие полуплоскости, которые соответствуют неравенствам (1) и (2). Прямая (1) делит координатную плоскость на две полуплоскости. Одна полуплоскость расположена выше прямой, вторая ниже. Чтобы найти ту полуплоскость, которая соответствует неравенству (1), необходимо взять любую точку, принадлежащую одной из полуплоскостей и подставить ее координаты в неравенство. Если неравенство будет верным, то данная полуплоскость является искомой.
Рис. 1.2. Графическое решение задачи о максимальной прибыли
Например, возьмем точку с координатами и подставим ее координаты в неравенство (1) . Получается - данное неравенство является верным, следовательно, неравенству (1) удовлетворяет полуплоскость, лежащая ниже прямой (1).
Аналогично, поступим для неравенства (2) . Возьмем точку с координатами . Получается - данное неравенство верно. Неравенству (2) удовлетворяет полуплоскость, расположенная ниже прямой (2). Стрелки на каждой границе показывают, с какой стороны прямой выполнены ограничения. Учитывая неравенства (3), получаем, что выделенный четырехугольник является областью, содержащей точки, для которых выполнены условия (1-3). Точки, лежащие внутри и на границе этой области, являются допустимыми решениями. Среди всех допустимых решений нужно найти оптимальное решение, при котором функция будет принимать максимальное значение.
Для поиска оптимального решения построим по функции прямую уровня.
Возьмем произвольную точку, принадлежащую области допустимых решений — четырехугольнику , например, точку с координатами . Подставим координаты точки в функцию .
Прямая уровня будет иметь следующий вид:
Построим полученную прямую. Для этого необходимо найти координаты двух произвольных точек этой прямой. Одна точка у нас уже есть — это точка . Найдем еще одну точку. Пусть , тогда . Следовательно, координаты дополнительной точки . Отметим полученные точки и построим прямую уровня (на рисунок 1.2 она обозначена (3)).
Значения функции будут возрастать по мере того, как прямая уровня удаляется от начала координат в положительном квадранте. Направление возрастания функции будет совпадать с вектором, координаты которого являются коэффициентами при переменных и функции . На рисунке — это вектор , отложенный от точки . Обратите внимание, что вектор , определяющий направление возрастания функции , всегда будет перпендикулярен прямой уровня.
gendocs.ru