Постановка задачи оптимизации. Постановка задачи оптимизации
54 Постановка задачи оптимизации
Задача оптимизации задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором лин. и/или нелин. равенств и/или неравенств.
Суть методов оптимизации (оптимального программирования) заключается в том, чтобы, исходя из наличия определенных ресурсов, выбрать такой способ их использования (распределения), при котором будет обеспечен максимум или минимум интересующего показателя
Оптимизация – это целенаправленная деятельность, которая заключается в получении наилучших результатов при соответствующих условиях.
Постановка задачи оптимизации:
Включает 2 объекта:
целевая ф-ция f(x) где х (x1, x2, … , xn)
определяется область допустимых значений D xD
Требуется f(x) min (max) xD
Классификация задач оптимизации:
без ограничений f(x,y) = (x - 1)2 + (y - 3)2 + 1
с ограничениями
напр f(x,y)= x2 + y2
Если целевая ф-ция f(x) и ф-ция описывающая ограничения на аргументы целевой ф-ции, являются линейными ф-циями своих аргументов, то задача оптимизации называется задачей линейного программирования.
Если целевая ф-ция или хотя бы 1 из уравнений, описывающих ограничения, является нелинейной ф-цией своих аргументов, то задача оптимизации называется задачей нелинейного программирования.
Итак, для решения задачи оптимизации необходимо:
а) составить математическую модель объекта оптимизации,
б) выбрать критерий оптимальности и составить целевую функцию,
в) установить возможные ограничения, которые должны накладываться на переменные,
г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.
55 Решение оптимизационных задач в системе ms Excel
Для этой цели в Excel имеется инструмент Поиск решений
Определим функцию пользователя
- ПФЛ (пользоват-я функция листа)
- ПФЛ
|
| B | C | D |
| 11 | x | y | F(x,y) |
| 12 | 2 | 1 | формула для F(x, y) |
Столбцы В и С – начальные значения для переменных x, y
Для нахождения экстремума всегда надо указывать начальное приближение.
D12→MyF(B12;C12) или = B12^3+C12^3-9*B12*C12+1
C16→MyF(B12;C12) или = (B12-4)^2+(C12-4)^2
Выполнить команду Меню Сервис→Поиск решения
Установить целевую ячейку D12, равное min знач , max знач =0 изменяя значения ячейки В12, С12
«ДОБАВИТЬ»
Вводим ограничения
$C$16=16
Ссылки
С16 далее выбираем значения ≥ либо ≤ и др
Ставим значение ограничения и выбираем ОК, затем ВЫПОЛНИТЬ.
Если решение найдено, то из предложенных форм отчета выбрать РЕЗУЛЬТАТ. В итоге в книгу Exel будет добавлен специальный лист, который будет называться отчет 1 и т.д.
Пример задачи линейного программирования
2Х1+3Х2→min
|
| B | C | D |
| 1 | x | y | F(x,y) |
| 2 | 0 | 0 |
|
В столбце D указывается формула для расчета F(x,y) т.е. 2*В2+3*С2,
Выполнить команду Меню Сервис→Поиск решения
Целевая ячейка D2, добавить ограничения→ВЫПОЛНИТЬ
studfiles.net
Постановка задачи оптимизации
Предприятие изготавливает топливные смеси трех видов (ТС1, ТС2, ТС3), в состав которых входит торф, уголь и горючий сланец.
Имеется возможность закупить 400 т торфа, 250 т угля и 350 т горючего сланца.
Для изготовления топливных смесей торф, уголь и горючий сланец смешиваются в следующих пропорциях: ТС1 - 3:5:2, ТС2 - 1:2:1, ТС3 - 2:2:1.
Для выполнения имеющихся заказов необходимо выпустить не менее 20 т топливной смеси ТС1.
Топливные смеси ТС2 и ТС3 должны выпускаться в соотношении 1:10.
Торф закупается по цене 320 ден.ед./т, уголь - 800 ден.ед./т, горючий сланец - 500 ден.ед./т.
Топливные смеси продаются по следующим ценам: ТС1 - 1200 ден.ед./т, ТС2 - 1000 ден.ед./т, ТС3 - 1500 ден.ед./т.
Составить план выпуска топливных смесей, обеспечивающий предприятию максимальную прибыль.
Построение базовой аналитической модели
Составим аналитическую модель задачи, для этого введем переменные:
Х1 – количество произведенной топливной смеси ТС1;
Х2 – количество произведенной топливной смеси ТС2;
Х3 – количество произведенной топливной смеси ТС3;
Введём ограничения.
Имеется возможность закупить 400 т торфа, 250 т угля и 350 т горючего сланца.
Для изготовления топливных смесей торф, уголь и горючий сланец смешиваются в следующих пропорциях: ТС1 - 3:5:2, ТС2 - 1:2:1, ТС3 - 2:2:1
0,3 Х1+0,25 Х2+0,4 Х3400
0,5 Х1+0,5 Х2+0,4 Х3250
0,2 Х1+0,25 Х2+0,2 Х3350
Для выполнения имеющихся заказов необходимо выпустить не менее 20 т топливной смеси ТС1.
Х1 ≥ 20
Топливные смеси ТС2 и ТС3 должны выпускаться в соотношении 1:10.
10Х2 = Х3
Составим целевую функцию.
Прибыль от продажи смесей: ТС1 - 1200 ден.ед./т, ТС2 - 1000 ден.ед./т, ТС3 - 1500 ден.ед./т.
1200Х1
1000Х2
1500Х3
Затраты на закупку сырья: торф-320 ден.ед./т, уголь - 800 ден.ед./т, горючий сланец - 500 ден.ед./т.
315Х1
312,5Х2
330Х3
Таким образом, получаем
Е = 885Х1 +687,5Х2 +1170Х3 – это прибыль предприятия, которую необходимо максимизировать.
Математическая модель имеет вид:
10Х2 = Х3
0,3 Х1+0,25 Х2+0,4 Х3400
0,5 Х1+0,5 Х2+0,4 Х3250
0,2 Х1+0,25 Х2+0,2 Х3350
Х1 ≥ 20
Хi 0, i = 1..3
Е = 885Х1 +687,5Х2 +1170Х3 max
Обоснование вычислительной процедуры
Для большинства методов решения задач линейного программирования требуется предварительно привести задачу к стандартной форме. Задача (или ее математическая модель) представлена в стандартной форме, если она соответствует следующим условиям:
целевая функция подлежит максимизации;
все ограничения имеют вид равенств;
на все переменные накладываются ограничения неотрицательности.
Для решения данной задачи воспользуемся симплекс- методом. Так как в математической модели присутствуют ограничения вида «равно», то для решения задачи потребуется методы искусственного базиса. Поиск целочисленного решения не требуется, так как все переменные задачи по своему физическому смыслу могут принимать нецелочисленные значения.
ПРИНЦИП РАБОТЫ СИМПЛЕКС - МЕТОДА
Симплекс-метод позволяет решать задачи линейного программирования любой размерности, т.е. с любым количеством переменных. Решение задач линейного программирования на основе симплекс-метода состоит в целенаправленном переборе угловых точек ОДР в направлении улучшения значения целевой функции.
Можно доказать, что экстремум (минимум или максимум) целевой функции всегда достигается при значениях переменных X1, X2,...,Xn, соответствующих одной из угловых точек ОДР. Другими словами, оптимальное решение всегда находится в угловой точке ОДР.
Принцип работы симплекс- метода состоит в следующем. Находится какое- либо допустимое решение, соответствующее одной из угловых точек ОДР. Проверяются смежные с ней угловые точки ОДР. Если ни в одной из смежных угловых точек значение целевой функции не улучшается, то решение задачи завершается; текущая угловая точка ОДР соответствует оптимальному решению задачи. Если имеются смежные угловые точки ОДР, для которых значение целевой функции улучшается, то выполняется переход в ту из них, для которой достигается наиболее быстрое улучшение значения целевой функции. Для новой угловой точки ОДР процесс повторяется, т.е. проверяются смежные угловые точки. Перебор угловых точек происходит до тех пор, пока не будет найдено оптимальное решение, т.е. пока не будет достигнута угловая точка ОДР, для которой ни в одной из смежных точек значение целевой функции не улучшается.
Поиск решения на основе симплекс-метода реализуется путем вычислений на симплекс-таблицах. Основные этапы реализации симплекс- метода следующие.
Задача линейного программирования приводится к стандартной форме.
Определяется начальное допустимое решение (начальная угловая точка ОДР).
Строится исходная симплекс- таблица. Выполняются преобразования симплекс-таблиц, соответствующие перебору угловых точек ОДР, до получения оптимального решения.
Реализация симплекс- метода существенно различается в зависимости от вида математической модели задачи. В задаче также есть ограничение вида “больше либо равно”, следовательно, придется воспользоваться методом искусственного базиса (будем использовать двухэтапный метод).
В данной задаче все переменные по своему физическому смыслу могут принимать дробные значения, поэтому ограничения целочисленности на них не накладываются.
studfiles.net
Постановка задачи оптимизации
Автозавод выпускает автомобили двух моделей: «Шторм» и «Торнадо». На заводе работает 1000 неквалифицированных и 800 квалифицированных рабочих, работающих по 40 ч в неделю. Для производства одного автомобиля «Шторм» требуется 30 ч неквалифицированного и 50 ч квалифицированного труда, для производства автомобиля «Торнадо» - 40 ч неквалифицированного и 20 ч квалифицированного труда. Для выпуска каждого автомобиля «Шторм» требуются затраты в размере 1500 ден. ед. на сырье и комплектующие, для каждого автомобиля «Торнадо» - 500 ден. ед. Суммарные затраты на сырье и комплектующие не должны превосходить 900 тыс. ден. ед. в неделю. Рабочие, осуществляющие доставку автомобилей торговым организациям, работают по пять дней в неделю и могут вывезти с автозавода не более 210 автомобилей в день.
Каждый автомобиль «Шторм» приносит автозаводу прибыль в размере 1000 ден.ед., каждый автомобиль «Торнадо» - 500 ден. ед.
Составить план выпуска автомобилей, обеспечивающий автозаводу максимальную прибыль.
Построение базовой аналитической модели
В данной задаче необходимо составить план выпуска автомобилей, обеспечивающий автозаводу максимальную прибыль.
Для построения математической модели задачи введем переменные. Обозначим:
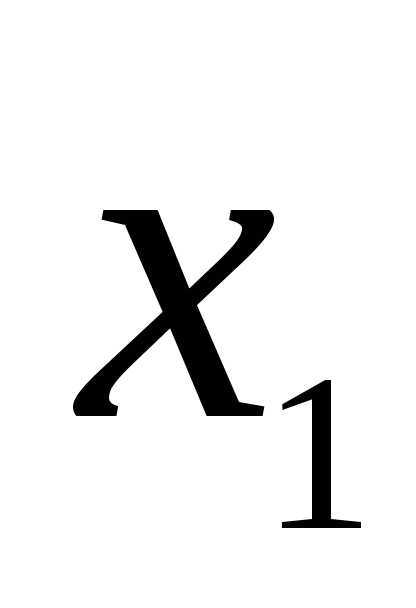–количество автомобилей «Шторм»;
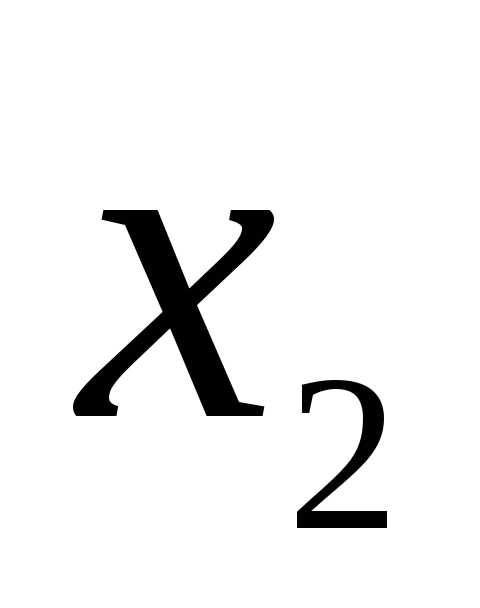–количество автомобилей «Торнадо»;
Поскольку по условию каждый рабочий работает по 40 ч в неделю, то получаем 40*1000=40000 ч неквалифицированного труда в неделю и 800*40=32000 ч квалифицированного труда. В неделю с предприятия вывозят 210*5=1050 автомобилей.
Так как для производства одного автомобиля "Шторм" требуется 30 ч неквалифицированного и 50 ч квалифицированного труда, для производства автомобиля "Торнадо" - 40 ч неквалифицированного и 20 ч квалифицированного труда, то
Так как для выпуска каждого автомобиля "Шторм" требуются затраты в размере 1500 ден. ед. на сырье и комплектующие, для каждого автомобиля "Торнадо" - 500 ден. ед. и суммарные затраты на сырье и комплектующие не должны превосходить 900 тыс. ден. ед. в неделю, то
.
Так как рабочие, осуществляющие доставку автомобилей торговым организациям, могут вывезти с автозавода не более 1050 автомобилей в неделю, то
Кроме того, переменные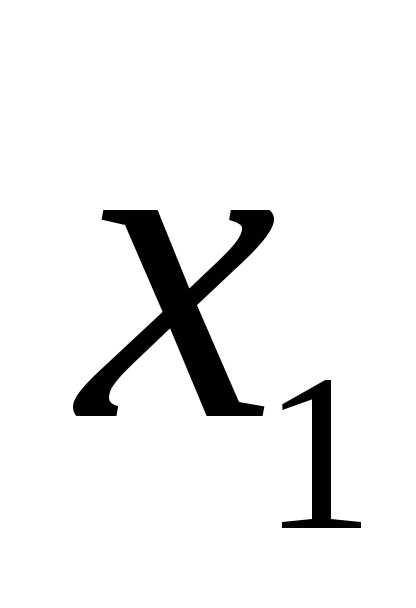 
, 
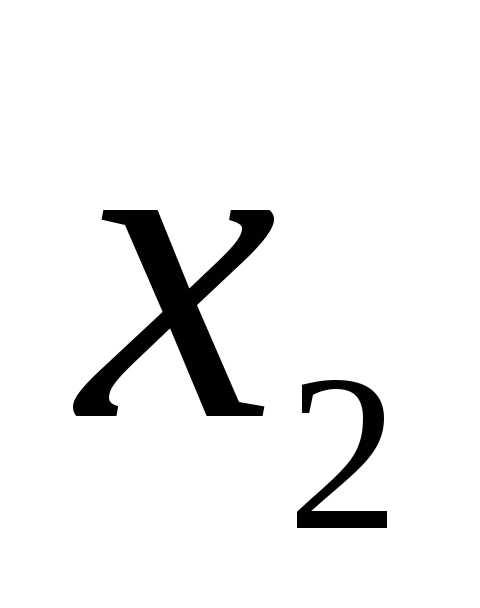по своему физическому смыслу не могут принимать отрицательных и дробных значений, так как обозначают количество автомобилей. Поэтому необходимо указать ограничения неотрицательности: и целочисленности.
В данной задаче необходимо составить план выпуска автомобилей, обеспечивающий автозаводу максимальную прибыль:
Величина является целевой функцией, которая должна быть максимальной:
Приведем полную математическую модель рассматриваемой задачи:
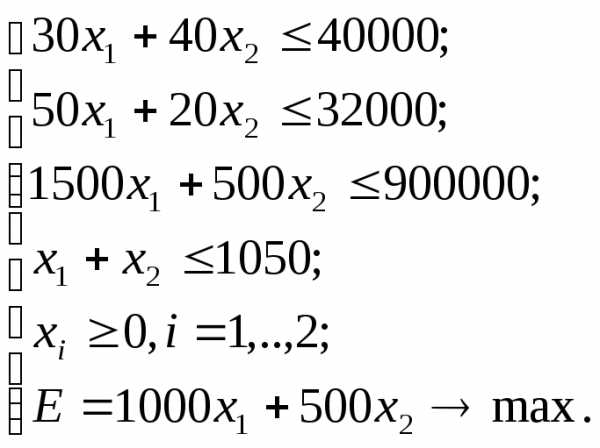
Обоснование вычислительной процедуры
Все ограничения и целевая функция в данной задаче линейны, поэтому для ее решения можно использовать симплекс-метод. В математической модели задачи нет ограничений «больше или равно». Поэтому для решения задачи не требуется использовать метод искусственного базиса.
Все переменные в задаче по своему физическому смыслу должны принимать неотрицательные и целые значения.
Решение задачи оптимизации на основе симплекс-метода
Приведем математическую модель задачи к стандартной форме. Для этого в ограничения «меньше или равно» введем остаточные переменные. Наша целевая функция подлежит максимизации:
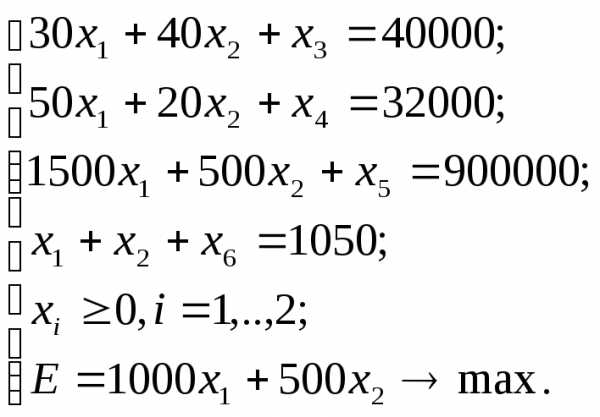
Переменные 
, 
– остаточные, отражают, насколько меньше по сравнению с максимальным допустимым значением будет затрачено неквалифицированного и квалифицированного труда соответственно. Переменная 
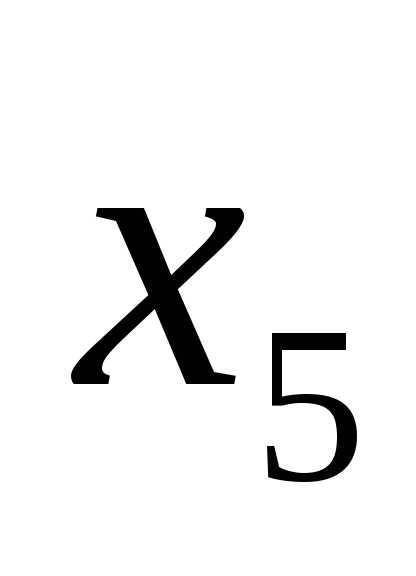– остаточная, отражает, насколько меньше по сравнению с максимальным допустимым значением составят суммарные затраты на сырье. Переменная 
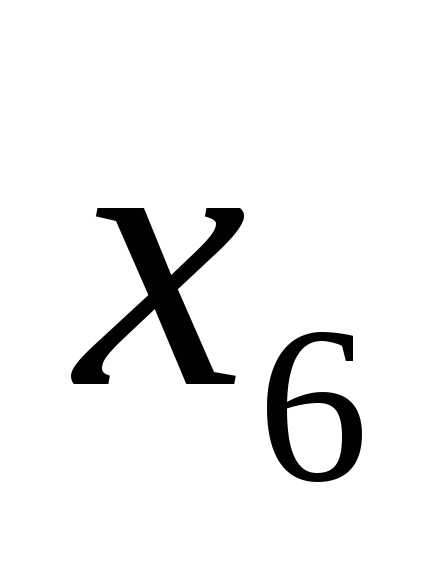– остаточная, отражает, насколько меньше по сравнению с максимальным допустимым значением будет вывезено автомобилей.
Составим первую симплекс-таблицу (таблица 1).
Таблица 1.
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | Решение |
| E | -1000 | -500 | 0 | 0 | 0 | 0 | 0 |
| x3 | 30 | 40 | 1 | 0 | 0 | 0 | 40000 |
| x4 | 50 | 20 | 0 | 1 | 0 | 0 | 32000 |
| x5 | 1500 | 500 | 0 | 0 | 1 | 0 | 900000 |
| x6 | 1 | 1 | 0 | 0 | 0 | 1 | 1050 |
Выбирается переменная для включения в базис: это переменная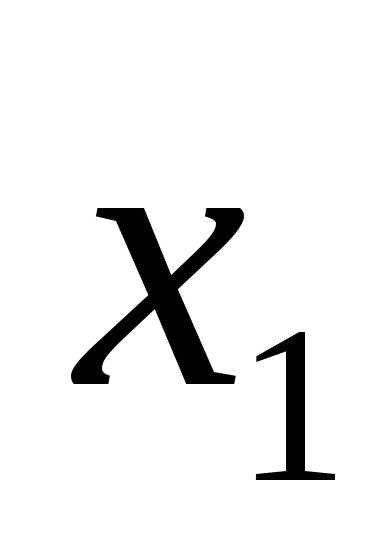 
, так как ей соответствует максимальный по модулю отрицательный коэффициент искусственной целевой функции.
Для определения переменной, исключаемой из базиса, найдем симплексные отношения. Минимальное симплексное отношение соответствует переменной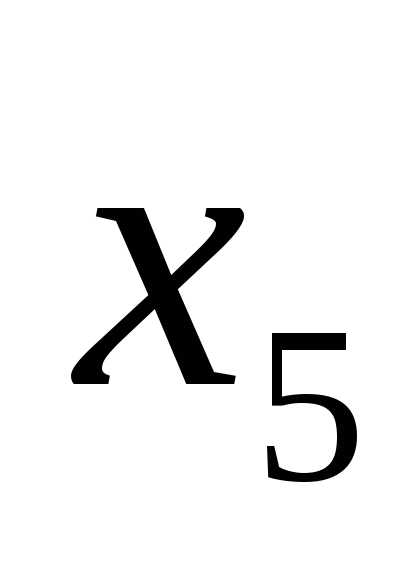 
, значит, эта переменная исключается из базиса.
В результате преобразований по правилам симплекс-метода будет получена следующая симплекс-таблица (таблица 2).
Таблица 2.
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | Решение |
| E | 0 | -166,67 | 0 | 0 | 0,67 | 0 | 600000 |
| x3 | 0 | 30 | 1 | 0 | -0,02 | 0 | 22000 |
| x4 | 0 | 3,33 | 0 | 1 | -0.03 | 0 | 2000 |
| x1 | 1 | 0,33 | 0 | 0 | 0 | 0 | 600 |
| x6 | 0 | 0,67 | 0 | 0 | 0 | 1 | 450 |
Выбирается переменная для включения в базис. Это переменная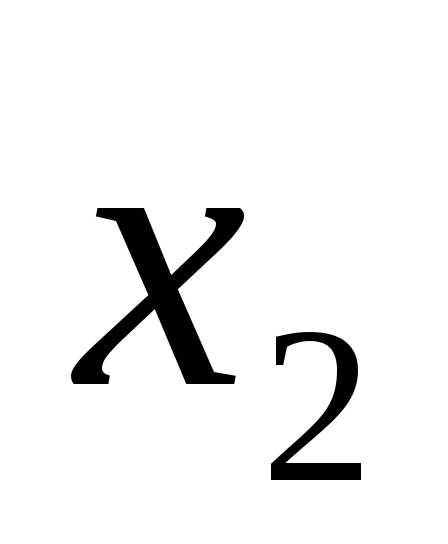 
, так как ей соответствует максимальный по модулю отрицательный коэффициент искусственной целевой функции.
Для определения переменной, исключаемой из базиса, найдем симплексные отношения: 22000/30=733,33; 2000/3,33=600,6; 600/0,33=1818,18; 450/0,67=671,64. Минимальное симплексное отношение соответствует переменной 
, значит, эта переменная исключается из базиса.
В результате преобразований по правилам симплекс-метода будет получена следующая симплекс-таблица (таблица 3):
Таблица 3.
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | Решение |
| E | 0 | 0 | 0 | 50 | -1 | 0 | 700000 |
| x3 | 0 | 0 | 1 | -9 | 0,28 | 0 | 4000 |
| x2 | 0 | 1 | 0 | 0,3 | -0,01 | 0 | 600 |
| x1 | 1 | 0 | 0 | -0,1 | 0 | 0 | 400 |
| x6 | 0 | 0 | 0 | -0,2 | 0,01 | 1 | 50 |
Выбирается переменная для включения в базис. Это переменная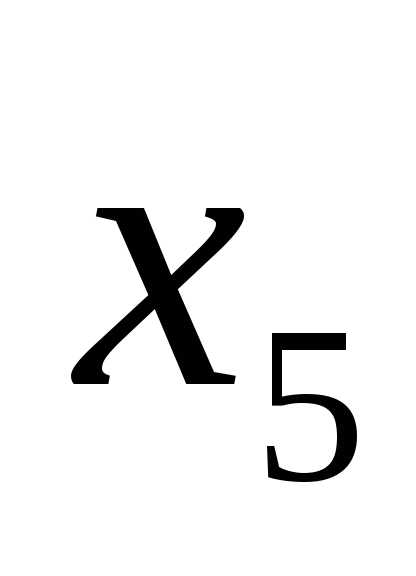 
, так как ей соответствует максимальный по модулю отрицательный коэффициент искусственной целевой функции.
Для определения переменной, исключаемой из базиса, найдем симплексные отношения: 4000/0,28=14285,71; 600/0,01=60000; 400/0=∞; 50/0,01=5000. Минимальное симплексное отношение соответствует переменной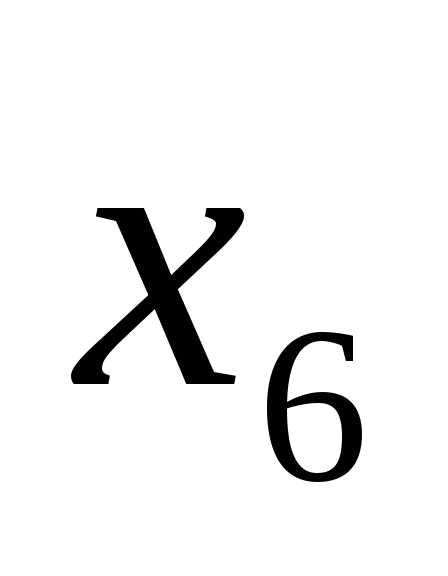 
, значит, эта переменная исключается из базиса.
В результате преобразований по правилам симплекс-метода будет получена следующая симплекс-таблица (таблица 4):
Таблица 4.
| Базис | x1 | x2 | x3 | x4 | x5 | x6 | Решение |
| E | 0 | 0 | 0 | 16,67 | 0 | 166,67 | 708333,33 |
| x3 | 0 | 0 | 1 | 0,33 | 0 | -46,67 | 1666,67 |
| x2 | 0 | 1 | 0 | -0,03 | 0 | 1,67 | 683,33 |
| x1 | 1 | 0 | 0 | 0,03 | 0 | -0,67 | 366,67 |
| x5 | 0 | 0 | 0 | -33,33 | 1 | 166,67 | 8333,33 |
Получено оптимальное решение (признак его оптимальности – отсутствие отрицательных элементов в строке целевой функции). Основные переменные приняли следующие значения: , . Это означает, что предприятию следует выпустить 366,67 автомобилей «Шторм» и 683,33 автомобиля «Торнадо». Значение целевой функции показывает, что при таком производстве прибыль составит 708333,33 ден. ед.
Переменные не приняли целочисленные значения, поэтому будем использовать метод ветвей и границ. В результате его использования было получено следующее оптимальное решение (Таблица 5):
Таблица 5.
| Минимум целевой функции равен 708000 | ||||||
| Переменная | X1 | X2 | X3 | X4 | X5 | X6 |
| Значение | 366 | 684 | 1660 | 20 | 9000 | 0 |
Получено оптимальное целочисленное решение.
Основные переменные задачи приняли следующие значения: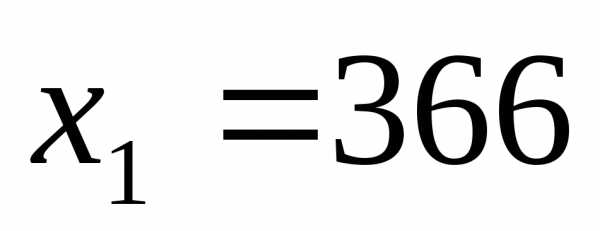 
ед.,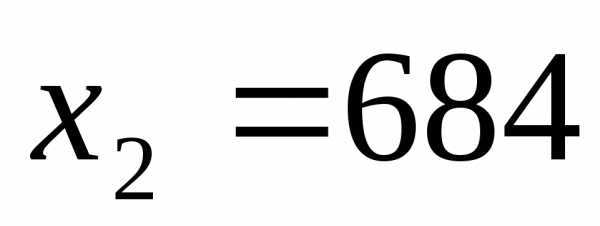 
ед. Это означает, что необходимо выпустить 366 автомобиля «Шторм» и 684 автомобиля «Торнадо». Значение целевой функции показывает, что максимально возможная прибыль составит 708000 ден. ед.
Остаточная переменная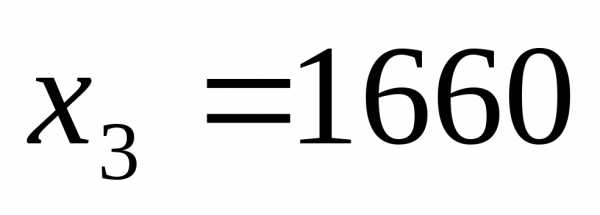 
означает, что труд неквалифицированных рабочих будет израсходован не полностью – на 1660 часов меньше максимально допустимого значения.
Остаточная переменная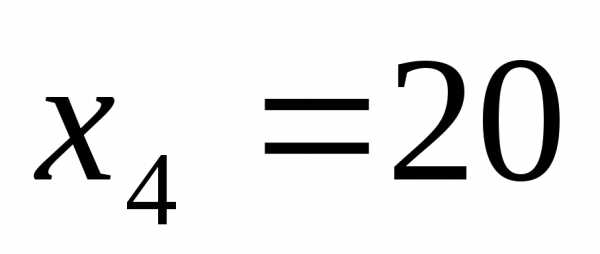 
означает, что труд квалифицированных рабочих будет израсходован не полностью – на 20 часов меньше максимально допустимого значения.
Остаточная переменная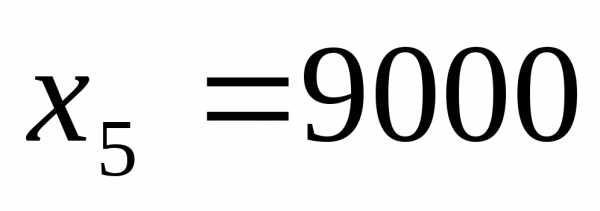 
означает, что будут израсходованы не все возможные ресурсы – на 9000 ден. ед. меньше максимально допустимого значения.
Остаточная переменная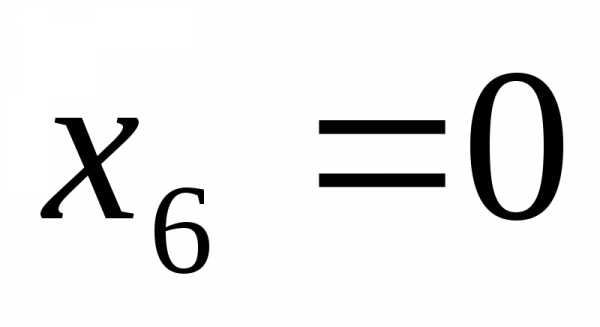 
означает, что будет произведено максимально возможное количество автомобилей – 1050 штук.
Рабочий лист с результатами решения задачи с использованием табличного процессора Excel приведен в приложении А.
studfiles.net
