Open Library - открытая библиотека учебной информации. Оптимизация методом неопределенных множителей лагранжа

1.-2. Постановка задачи

Лекция №9

Тема: «Методы и модели нелинейного программирования для исследования операций СТС»

План:

Задачи и общие понятия нелинейного программирования. Почему нелинейное? Переход от линейного программирования к нелинейному. Точность линейного решения, решение первого приближения для нерешения.
Общая задача Н.П.
Геометрическая интерпретация задач Н. П.
Экономическая задача Н. П.
Четыре класса задач Н.П.

В задаче нелинейного программирования требуется найти значение многомерной переменной х= (), минимизирующее целевую функцию f (x) при условиях, когда на переменную х наложены ограничения типа неравенств, i=1,2,…,m, а переменные, т.е. компоненты вектора х, неотрицательны:.

Иногда в формулировке задачи ограничения имеют противоположные знаки неравенств. Учитывая, однако, что если , то, всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например, то их можно представить в виде пары неравенств,, сохранив тем самым типовую формулировку задачи.

Метод неопределенных множителей Лагранжа

Условия экстремума функции, которые рассмотрены выше, позволяют найти, так называемый, безусловный экстремум. Однако, в большинстве практических задач принятия решения требуется принять решение - определить экстремум критерия оптимальности при условии, что на независимые переменные наложены ограничения, имеющие вид равенств. Типичными примерами подобных задач служат задачи, в которых требуется оптимальным образом распределить заданное количество ресурсов, чтобы принятая оценка эффективности процесса имела при этом максимальное или минимальное значение. Для решения таких задач в классическом анализе используется метод неопределенных множителей Лагранжа. Сами задачи получили название задач на условный экстремум.

Пусть требуется найти экстремум функции, например, минимум

Q (, при условии

Согласно методу Лагранжа для решения задач на условный экстремум функции составляется вспомогательная функция Лагранжа, которая определяется соотношением

где , = - неопределенные множители Лагранжа.

Таким образом, задача нахождения условного экстремума функции сводится к задаче нахождения безусловного экстремума функции, но число неизвестных в ней n + k (uι, ι = 1, n; λj, j = 1, k).

Как известно из п.1.2 необходимым условием безусловного экстремума функции является равенство нулю частных производных, которые для данного конкретного случая записываются в виде

и дает n уравнений для определения неизвестных. Эта система уравнений дополняется к уравнениям и, следовательно, получается (n + k) неизвестных и (n + k) уравнений.

Метод множителей Лагранжа дает лишь необходимые условия существования условного экстремума для непрерывных функций, имеющих также непрерывные производные, поэтому найденные значения переменных могут и не давать экстремума функции Q (u1,., un), их надо проверить с использованием достаточных условий экстремума функции многих переменных.

В окончательном решении задачи фактически множители Лагранжа не известны, поэтому задача совместного решения системы, иногда ставится как задача исключения "k" неизвестных переменных uι с последующим решением остающейся системы n уравнений с n неизвестными.

Задача Лагранжа имеет "n - k" степеней свободы.

2. Геометрическая интерпретация метода множителей Лагранжа

Интерес представляют геометрический смысл множителей Лагранжа. Для такой интерпретации лучше рассмотреть задачу с двумя неизвестными и одним ограничением.

Пусть требуется найти минимум функции при условии. Если минимум существует, то в пространстве функцияQ должна иметь вид воронки, а условие связи - это некоторая поверхность.

На рис.4, б изображены на плоскости переменных u1, u2 линии уровня функции Q (u1, u2) и ограничение φ (u1, u2) = 0, представляющее собой линию. Составляется вспомогательная функция Q (u1, u2) = Q (u1, u2) + λφ (u1, u2). Необходимое условие экстремума дает:

Рисунок 1.4 - Геометрический смысл множителей Лагранжа:

а - пространственное изображение;

б - изображение проекции на плоскость u2 - u1

или

В точке А - точке касания линии с линией равного уровня функциииимеют общую касательную и необходимое условие минимума представляет собой условие пропорциональности двух векторов: вектора - градиента функции и вектора- градиента функции

Два вектора пропорциональны друг другу лишь в том случае, если они коллинеарные. Так как градиент функции перпендикулярен касательной к линии уровня, то в точке А выполняется условие, и множитель является коэффициентом пропорциональности между векторами и

Рассмотрим задачу нелинейного программирования, содержащую только две переменные, записанную в виде

,…………….

(x) <, x = ().

Как уже отмечалось, функция f (x) называется целевой функцией, а неравенства , i= 1,.,m называются ограничениями задачи. Множество точек, удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.

Решить задачу нелинейного программирования графически - значит найти такую точку из допустимого множества, через которую проходит линия уровня f (,) = С, имеющая максимальное значение величины С из всех линий уровня, проходящих через допустимые точки задачи.

Как и в случае задач линейного программирования, для задач нелинейного программирования, содержащих только две переменные, возможна графическая интерпретация.

Наиболее существенное отличие задачи нелинейного программирования от линейных задач заключается в том, что оптимальное решение может находиться как на границе допустимого множества, так и являться его внутренней точкой.

Этапы графического решения задач нелинейного программирования можно сформулировать следующим образом.

Этап 1. На плоскости наносятся геометрические места точек, соответствующих каждому уравнению из ограничений задачи (x) =, i= 1,.,m. Строится допустимое множество задачи. Если допустимое множество задачи пусто, то задача не имеет решения.

Этап 2. Строятся линии уровня целевой функции f (,) = С при различных значениях параметра С.

Этап 3. Определяется направление возрастания (для задачи максимизации) или убывания (для задачи минимизации) линий уровня целевой функции.

Этап 4. Определяется точка допустимого множества, через которую проходит линия уровня с максимальным (для задачи максимизации) или минимальным (для задачи минимизации) значением параметра С. Если целевая функция не ограничена сверху (для задачи максимизации) или не ограничена снизу (для задачи минимизации) на допустимом множестве, то задача не имеет решения.

Этап 5. Для найденной точки определяют ее координаты = (,)и значение целевой функции в данной точке f= (,)

Решим следующую задачу нелинейного программирования, используя геометрическую интерпретацию

Построим линии, соответствующие ограничениям задачи и вычислим область определения функции (рис.3.1).

Рисунок 3.1 - Область определения функции

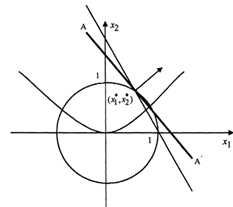
Рисунок 3.2 - Линия уровня функции

Линия уровня, соответствующая максимальному параметру С и проходящая через какую-либо точку допустимого множества, изображена на рисунке 3.2 АА’. Координаты оптимальной точки находятся из системы уравненийоткуда.

studfiles.net

1.4 Метод неопределенных множителей Лагранжа

Условия экстремума функции, которые рассмотрены выше, позволяют найти, так называемый, безусловный экстремум. Однако, в большинстве практических задач принятия решения требуется принять решение – определить экстремум критерия оптимальности при условии, что на независимые переменные наложены ограничения, имеющие вид равенств. Типичными примерами подобных задач служат задачи, в которых требуется оптимальным образом распределить заданное количество ресурсов, чтобы принятая оценка эффективности процесса имела при этом максимальное или минимальное значение.

Для решения таких задач в классическом анализе используется метод неопределенных множителей Лагранжа. Сами задачи получили название задач на условный экстремум.

1.4.1 Основные положения

Пусть требуется найти экстремум функции, например, минимум

Q(, при условии

где , =– неопределенные множители Лагранжа.

Как известно из п. 1.2 необходимым условием безусловного экстремума функции является равенство нулю частных производных, которые для данного конкретного случая записываются в виде

и дает n уравнений для определения неизвестных. Эта система уравнений дополняется к уравнениям и, следовательно, получается (n +k) неизвестных и (n +k) уравнений.

Метод множителей Лагранжа дает лишь необходимые условия существования условного экстремума для непрерывных функций, имеющих также непрерывные производные, поэтому найденные значения переменных могут и не давать экстремума функции Q (u1, ...,un), их надо проверить с использованием достаточных условий экстремума функции многих переменных.

В окончательном решении задачи фактически множители Лагранжа не известны, поэтому задача совместного решения системы, иногда ставится как задача исключения "k" неизвестных переменныхuι с последующим решением остающейся системыn уравнений сn неизвестными.

Задача Лагранжа имеет "n –k" степеней свободы.

1.4.2 Геометрическая интерпретация метода множителей Лагранжа

Пусть требуется найти минимум функции при условии. Если минимум существует, то в пространстве функцияQ должна иметь вид воронки, а условие связи – это некоторая поверхность.

На рис. 4, б изображены на плоскости переменныхu1,u2 линии уровня функцииQ (u1,u2) и ограничениеφ (u1,u2) = 0, представляющее собой линию. Составляется вспомогательная функцияQ (u1,u2) =Q (u1,u2) +λφ (u1,u2). Необходимое условие экстремума дает:

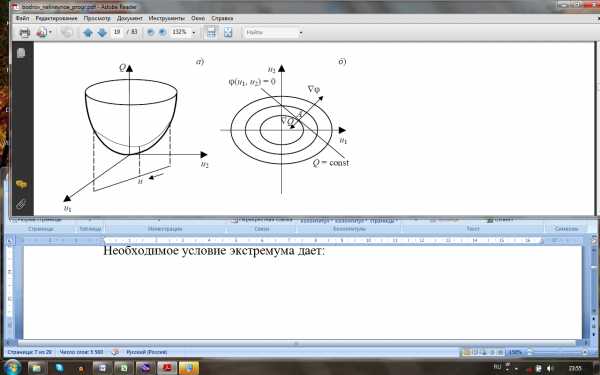
Рисунок 1.4 –Геометрический смысл множителей Лагранжа:

а – пространственное изображение;

б – изображение проекции на плоскость u2 – u1

или

В точке А – точке касания линиис линией равного уровня функциииимеют общую касательную и необходимое условие минимума представляет собой условие пропорциональности двух векторов: вектора – градиента функциии вектора– градиента функции

studfiles.net

3. Экономическая трактовка метода множителей Лагранжа

В некоторых задачах множители Лагранжа допускают и экономическое толкование. Если толковать целевую функцию Q (u1,., un) как прибыль, получаемую некоторым предприятием при использовании ресурсов, а условия k ограничения на дефицит ресурсов, то при (u1,., un) < 0 прибыль, то максимум целевой функции будет расти.

Экономист такую задачу будет решать следующим образом. Он назначит некоторые цены на единицы ресурсов и предложит потребителю купить их по этой цене. Последний, максимизируя чистую прибыль , найдет (u1,., un) и скажет, сколько ресурсов он хотел бы купить. В экономике почти всегда бывает так, что чем больше , тем меньше (u1,., un), и чем меньше , тем больше (u1,., un). Если окажется, что (u1,., un) > 0, то экономист повысит цену, если (u1,., un) < 0 - понизит. Так будет происходить до тех пор, пока при некоторой цене, называемой равновесной, потребителю будет выгодно, чтобы дефицит ресурсов (u1,., un) был равен нулю, при этом чистая прибыль будет максимальна, т.е. будут выполняться условия

Таким образом, равновесная цена с точностью до знака равна множителю Лагранжа.

4. Численные методы решения задач нелинейного программирования

Математическая формулировка задачи принятия решения эквивалентна задаче отыскания наибольшего или наименьшего значения функции одной или нескольких переменных. В большинстве практических задач критерий оптимальности Q (u), где u - вектор управляющих переменных, не может быть записан в явном виде, его значение обычно находится в результате решениясистемы уравнений математического описания оптимизируемого объекта. На независимые переменные могут быть наложены связи и ограничения как в виде равенств , так и в виде неравенств , которые, как правило, являются нелинейными и трудно вычислимыми соотношениями. Задачи такого типа являются предметом рассмотрения специального раздела математики, называемого нелинейным программированием. Обычно, решения задач нелинейного программирования могут быть найдены только численными методами.

Метод "золотого сечения"

Гораздо эффективнее, с точки зрения уменьшения затрат на вычисления, метод "золотого сечения": интервал неопределенности делится не пополам, как в методе дихотомии, а в определенном иррациональном соотношении

Это соотношение выполняется при

Метод заключается в том, что по заданным a и b как можно точнее определяется значение внутренней точки x1 (см. рис.2.6, б) по формуле

x1 = b - (b - a) / 1,618033989…

Рисунок 2.6 - Метод "золотого сечения": а - золотое сечение; б - геометрическое представление

Точка x2 определяется как точка, симметричная точке x1 на отрезке (a-b).

На основе анализа значений F1 = Q (x1) и F2 = Q (x2) интервал неопределенности сокращается путем отбрасывания из рассмотрения отрезка в котором экстремум исключен, исходя из условий уни-модальности Q (u). Далее мы определим симметричную точку внутри новых границ, вычисляем значение Q в этой точке, проводим анализ и т.д. до тех пор, пока разность между симметричными точками внутри интервала неопределенности больше . Блок-схема алгоритма метода "золотого сечения" представлена на рис.2.7.

Рисунок 2.7 - Блок-схема метода "золотого сечения"

studfiles.net

Метод неопределенных множителей Лагранжа

В классическом анализе этот метод ориентирован на решение задач на условный экстремум, когда условия имеют вид равенств:

f(X) ® extr, i(X)=0, i=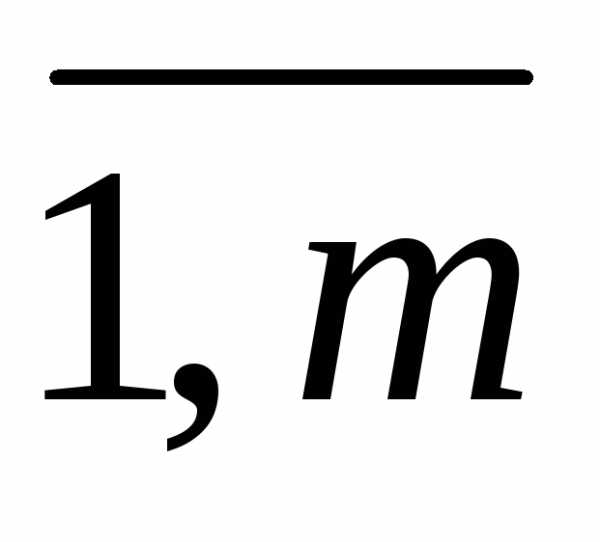. (3.17)

Очевидно, что задача (3.17) имеет смысл при m<n, когда система равенств имеет неединственное решение. В предыдущем разделе к таким задачам применялся метод подстановки (исключения зависимых переменных), который сводит исходную задачу к задаче на безусловный экстремум с меньшим числом переменных. На первый взгляд может показаться, что это очень удобный прием. Но на практике далеко не всегда можно разрешить m уравнений относительно m переменных, а в тех случаях, когда это возможно, получающиеся выражения часто оказываются слишком сложными.

Метод множителей Лагранжа тоже преобразует исходную задачу в задачу на безусловный экстремум, но, в противоположность предыдущему методу, за счет увеличения числа неизвестных.

Для лучшего понимания сути метода сначала покажем, как получаются необходимые условия условного экстремума в задаче с двумя переменными, а затем сделаем обобщение.

Итак, найдем экстремум функции f(x1,x2) при условии

(x1,x2)=0. (3.18)

Этим равенством задается допустимая область D, в которой одна из переменных становится зависимой. Пусть зависимой переменной будет x2. В стационарной точке производные первого порядка по независимым переменным равны нулю. В нашем случае имеется только одна независимая переменная - x1, поэтому в нуль обращается полная производная целевой функции по x1. Используя правила дифференцирования неявной функции, получаем:

(3.19)

где - частные производные поx1 и x2 соответственно.

В области D функция постоянна, следовательно, производная этой функции по независимой переменной равна нулю:

(3.20)

В точке экстремума выполняются одновременно условия (3.19) и (3.20). Исключая из них , приходим к равенству

которое показывает, что в точке условного экстремума соблюдается равенство отношений частных производных целевой функции и функции условия по одноименным переменным. Обозначим это отношение постоянной . Полученное равенство

можно представить в виде

(3.21)

Таким образом, в точке условного экстремума необходимо выполнение условий (3.21). Но они содержат три неизвестных при двух равенствах. Добавляя к ним исходное условие задачи (3.18), получаем три уравнения с тремя неизвестными. К такому же результату мы придем, если будем решать задачу на безусловный экстремум расширенной целевой функции вида

. (3.22)

Действительно, взяв производные F по x1 и x2 и приравняв их нулю, получим равенства (3.21), а =0 дает (3.18). Новая функцияF называется функцией Лагранжа, а неизвестная постоянная -неопреде-ленным множителем Лагранжа.

Данная задача имеет простую геометрическую интерпретацию. На рис. 3.5 показаны линии равного уровня функции f и допустимая область, представляющая собой кривую, на которой (x1,x2)=0. Безусловный экстремум находится в точке B, а условный - в точке A, в которой касательные к линии уровня и к кривой =0 совпадают. Следовательно, в точке условного экстремума производные dx1/dx2 для функций f и равны, что и было получено выше (формулы (3.19) и (3.20)).

Канторович Л.В. придает множителю экономический смысл. Если подf(X) понимать доход, соответствующий плану выпуска продукции X, а под (X) - ограничение на издержки ресурса, тоимеет смысл «цены» этого ресурса: доказывается, что производная оптимального значения функцииf по ограничению с точностью до знака равна . Иначе говоря, множитель Лагранжа характеризует влияние изменения ресурса на оптимальное значение критерия. В такой трактовкеназываютмаргинальной оценкой ресурса (в теории двойственности является двойственной переменной).

Можно показать, что и в общем случае справедлив такой подход. Опуская доказательства, приведем окончательный результат. Для задачи (3.17) функция Лагранжа записывается в виде

(3.23)

где - вектор неопределенных множителей Лагранжа размерностиm. Отсюда следует, что функция Лагранжа представляет собой сумму целевой функции и парных произведений множителей на левые части условий. Необходимые условия по X дают n уравнений:

Добавляя к ним m равенств , получаем полную систему уравнений для отысканияn+m неизвестных.

Несмотря на увеличение числа неизвестных этот подход приводит к более простой системе уравнений, чем при использовании метода исключения переменных, и поэтому более предпочтителен. К функции Лагранжа, естественно, приложимы также достаточные условия экстремума (3.5),(3.6).

Применение метода Лагранжа проиллюстрируем двумя примерами. Первый пример призван показать технику и преимущество метода. Пусть требуется найти максимум функции f=x1+x2+x1x2 при условии

(3.24)

Сначала применим метод исключения. Из (3.24) выразим x2

и, подставив в целевую функцию, получим

В результате пришли к задаче на безусловный максимум функции одной переменной. Взяв производную по x1 и приравняв ее нулю, после элементарных преобразований имеем

Способ нахождения x1 из этого уравнения не очевиден. Даже в такой простой задаче применение метода исключения вызывает затруднения.

Теперь воспользуемся методом Лагранжа. Для нашей задачи функция Лагранжа записывается в виде

Необходимые условия дают два уравнения:

которые при фиксированном представляют собой линейную систему с двумя неизвестными. В данном случае она решается особенно просто: из симметрии относительно переменных следует, что в стационарной точке они равны между собой. Поэтому сразу имеем

Подставив это выражение в (3.24), получаем

или .

Таким образом, условный экстремум может достигаться в точках

Легко проверить, что положительные значения соответствуют максимуму при любом R, а отрицательные - минимуму только в определенном интервале R. (Убедиться в этом можно, записав достаточные условия экстремума функции F по переменным x1 и x2.)

Во втором примере рассмотрим одну из типичных задач исследования операций и увидим, что даже в общем случае применение метода множителей Лагранжа оказывается полезным, приводя к интересным качественным результатам.

Задача распределения ресурсов. В системе имеется m видов ресурсов в количестве 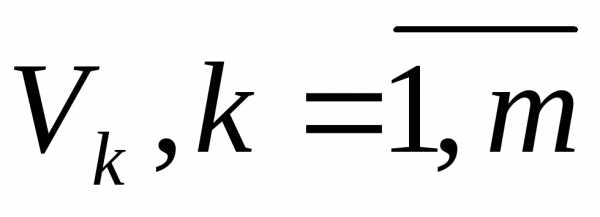, иN предприятий, нуждающихся в этих ресурсах. Однако ресурсов недостаточно для удовлетворения каждого предприятия оптимальным образом. Прибыль предприятия зависит как от количества выделяемых ему ресурсов, так и от управления на уровне предприятия:

Здесь vi =(vi1,vi2,...,vim) - вектор ресурсов, выделяемых i-му предприятию; ui=(ui1,ui2,...,uiv) - вектор индивидуальных управлений i-го предприятия. Необходимо так распределить имеющиеся ресурсы, чтобы суммарная прибыль предприятий была максимальной.

Модель задачи имеет вид:

, (3.25)

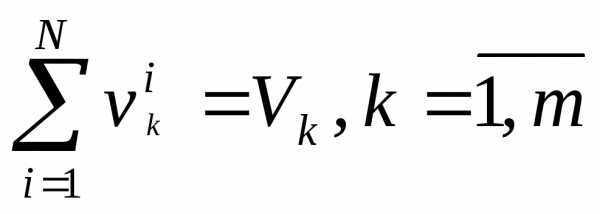, (3.26)

. (3.27)

Допустимое множество управлений Di не задано в явном виде, и его свойства не оговариваются.

Реальные задачи такого типа из-за их большой сложности не удается решать «в лоб». Поэтому задачу разбивают, если это возможно, на ряд более простых задач. Такой прием называют декомпозицией задачи. В нашем случае декомпозиция возможна, так как в задаче (системе) явно просматриваются два уровня принятия решений: на верхнем уровне распределяются все ресурсы исходя из цели системы в целом, а на нижнем каждое предприятие стремится использовать выделяемые ему ресурсы наилучшим образом в собственных интересах (рис. 3.6). Следовательно, при таком разбиении имеем одну задачу верхнего уровня и N задач нижнего уровня.

Но задачи обоих уровней связаны между собой: для решения задач одного уровня надо знать решение другого. Выйти из замкнутого круга можно в тех случаях, когда удается найти параметрическое решение задач одного из уровней. В рассматриваемой системе таким является нижний уровень.

Каждая из N задач нижнего уровня ставится так: найти зависимость максимальной прибыли предприятия от выделяемых ему ресурсов. Для этого нужно решить задачу

(3.28)

для всех возможныхvi. Метод решения задачи (3.28) здесь не рассматриваем, так как он может быть выбран только при явном задании модели. В результате решения этой задачи получим искомые функции и ui(vi). Тогда задача (3.25)-(3.27) преобразуется в задачу верхнего уровня

, (3.29)

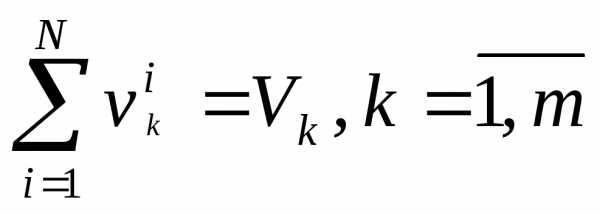. (3.30)

Если функции дифференцируемы (что будем предполагать), то к этой задаче применим метод множителей Лагранжа. Расширенная функция (функция Лагранжа) задачи (3.29),(3.30) имеет вид

(3.31)

Необходимые условия экстремума функции F дают систему mN уравнений

которую перепишем в виде

. (3.32)

Так как правая часть в (3.32) не зависит от i, то из этой системы следует цепочка равенств

. (3.33)

Из каждой цепочки составляется N-1 независимых равенств, то есть всего получаем m(N-1) уравнений, содержащих mN искомых величин . Недостающиеm уравнений дают исходные условия (3.30). Если система (3.33) нелинейна, то нахождение стационарных точек становится весьма проблематичным. Однако независимо от разрешимости системы (3.33),(3.30) мы можем сделать важный вывод, дающий качественное представление о свойствах оптимального распределения. Действительно, из (3.33) следует, что при оптимальном распределении ресурсов производные критериев всех потребителей по одному и тому же ресурсу равны между собой. Чтобы лучше понять смысл этого свойства, вспомним, что производная есть предел отношения приращения функции к приращению аргумента. Следовательно, при оптимальном распределении ресурсов реакция (изменение критерия) всех потребителей ресурсов на малое изменение одного и того же ресурса одинакова. Этот вывод справедлив для любых систем распределения рассмотренного класса. В частности, при распределении одного ресурса полученное свойство позволяет решить задачу графическим способом (рис.3.7): решение соответствует точкам на графиках функций , в которых касате-льные параллельны и.

Подводя итог рассмотрению методов классического анализа, отметим, что они могут применяться для решения задач оптимизации небольшой размерности и с простой структурой множества D. Задачи математического программирования, к которым сводится большинство задач исследования операций, требуют более мощных методов. Изучению этих методов посвящены главы 4-9.

Для закрепления пройденного материала в следующем разделе предлагается самостоятельно исследовать две задачи, одна из которых рассматривалась в разделе 3.1.

studfiles.net

Неопределенный множитель Лагранж - Справочник химика 21

Метод неопределенных множителей Лагранжа [c.5]

Классические методы решения экстремальных задач. К числу классических математических методов определения экстремума функции многих переменных относятся 1) метод поиска оптимума путем решения системы нелинейных уравнений, полученных при приравнивании нулю частных производных минимизируемой функции по оптимизируемым параметрам 2) метод неопределенных множителей Лагранжа. В математическом плане оба метода достаточно хорошо известны, поэтому основ- [c.122]

Поскольку общая методика решения задачи оптимального поэлементного резервирования ХТС состоит в том, что неравенства для ограничений (8.2) или (8.6) заменяют равенствами, а затем проводят поиск минимума или максимума КЭ, то для поиска экстремума КЭ (8.1) или (8.5) можно применить метод неопределенных множителей Лагранжа. Идея метода заключается в следующем. [c.208]

Основной недостаток метода штрафных функций—трудности, которые возникают в вычислительном процессе, когда параметры приближаются к предельным значениям. Это обусловлено появлением разрывов непрерывности вблизи границы допустимой области и связанной с ними плохой обусловленности гессиана целевой функции. Для устранения этого недостатка оказывается полезно комбинировать метод штрафных функций с методом неопределенных множителей Лагранжа. Новый метод получил название метода модг-фицированной, или расширенной функции Лагранжа. [c.215]

Модификацией метода простого перебора является метод динамического программирования, сущность которого изложена в разделе 8.2.4. Показано [231, 237], что этот метод чрезвычайно точен, поскольку его применение позволяет рассматривать все возможные решения. Однако к недостаткам указанного метода следует отнести то, что он весьма трудоемок и требует большого объема памяти ЭВМ. В связи с этим рекомендуют [237] комбинировать менее точные, но более простые методы неопределенных множителей Лагранжа и наискорейшего спуска с методом динамического программирования при получении нецелочисленного решения для оптимального вектора состава поэлементного резерва— применять метод неопределенных мно- кителей Лагранжа, при получении целочисленного решения из нецелочисленного округлением — воспользоваться методом динамического программирования. [c.207]

Таким образом, составив функцию Ф и приравняв ее производные по X и А, нулю, получим систему уравнений ( 1-3), решение которой даст оптимальные х] и значения неопределенных множителей Лагранжа. [c.178]

Получим теперь соотношения, к которым приводит применение метода неопределенных множителей Лагранжа (см. стр. 176), Рассматривая у )авнение (УП,544) как ограничение типа равенств, со- [c.408]

Для решения этой задачи можно воспользоваться методом неопределенных множителей Лагранжа (стр. 139). Составляя вспомогательную функцию [c.537]

Для поиска экстремума простых дифференцируемых функций, когда на переменные наложены условия типа равенств, часто используют метод неопределенных множителей Лагранжа- Если переменные связаны условиями [c.178]

Для решения указанной задачи оптимизации можно применить метод неопределенных множителей Лагранжа. [c.108]

Метод неопределенных множителей Лагранжа, который подробно рассмотрен в разделе 8.2.2, прост и удобен для решения задач оптимизации резервирования ХТС с использованием ЭВх 1. Однако он имеет следующие существенные недостатки. Во-первых, в процессе решения как прямой, так и обратной задачи оптимизации резервирования могут получиться нецелочисленные значения Х1. Поэтому возникает необходимость округления этих значений до ближайших целых чисел. При таком округлении возможны многочисленные варианты составов поэлементного резерва ХТС, перебор которых для выявления наилучшего варианта оказывается трудоемким процессом, требующим больших затрат времени [126, 237]. [c.205]

Практически часто бЕ>шает трудно, а иногда и вообще невозможно аналитически решить систему уравнений (IV,2) относительно некоторых неременных, т. е. представить ее в виде соотношений (1V,3). Поэтому для решения задач отыскания экстремума функции многих иеременнь[х (IV,I) с ограничениями на независимые переменные (IV,2) обычно используют метод неопределенных множителей Лагранжа, вывод основных соотношений которого рассмотрен ниже. [c.140]

Рассмотрим применение метода неопределенных множителей Лагранжа к решению обратной задачи оптимального резервирования ХТС. При поиске решения обратной задачи ограничение [c.212]

Метод неопределенных множителей Лагранжа прост и удобен для реализации на современных ЦВМ, но имеет ряд существенных недостатков. В связи с этим предложен [126] улучшенный в отношении скорости приближения к экстремуму КЭ модифицированный метод. Данный метод является параметрическим обобщением метода неопределенных множителей Лагранжа для случая дискретных переменных [126]. [c.214]

Для решения экстремальной задачи уровня Л,- — задачи определения оптимального варианта резерва ХТС — используют метод неопределенных множителей Лагранжа (см. раздел 8.2.2). [c.226]

Минимизация проводится с учетом уравнений (У-74), играющих роль ограничений типа равенств. Эта задача может быть решена методом неопределенных множителей Лагранжа. [c.132]

Решение поставленной изопериметрической вариационной задачи (П.1.1) —(П.1.4) будем искать методом неопределенных множителей Лагранжа. Выбираем функцию Лагранжа в виде [c.224]

Такую экстремальную задачу с дополнительными условиями можно решить методом неопределенных множителей Лагранжа. Умножим дополнительное условие (27.3) на неопределенный, но постоянный коэффициент (27.4) на 2 и (27.5) на Лз . Затем вычтем эти уравнения из (27.2). Используя (27.1), получим [c.140]

Используем вновь метод неопределенных множителей Лагранжа . Умножим первое дополнительное условие [c.251]

При минимизации целевой функции (2.27) на переменные w,DnH нагадываются следующие ограничения процесс при оптимальных значениях w,DuH должен обеспечивать заданную степень очистки х и расход по очищаемому газу Q. Таким образом, задача может быть решена мегодом неопределенных множителей Лагранжа [65] при учете двух функций ограничения f [c.68]

ГЧе Л, и - неопределенные множители Лагранжа. [c.69]

Наиболее распространенным методом учета дополнительных условий такого вида является метод неопределенных множителей Лагранжа. Пусть Р,Я = 1,2,. .., N есть набор некоторых комплексных чисел, [c.45]

В настоян ее время для решения оптимальных задач применяют в основном следую1цие методы 1) методы исследования функций классического анализа 2) методы, основанные на использовании неопределенных множителей Лагранжа 3) вариационное исчисление 4) динамическое программирование 5) принцип максимума 6) лгшеГнше программирование 7) нелинейное программирование. [c.29]

Для решения экстремальных задач с такими ограничениями в классическом анализе разработан и используется метод неопределенных множителей Лагранжа , сводящий задачу с ограничениями к обычной э1 стремальиой задаче без ограничений, что позволяет применить для ее решения приемы, рассмотренные в главе HI. В этом смысле настояш,ая глава является логическим продолжением предыдущей. Метод же множителей Лагранжа дает возможность иногда нсноль-зовать более эффективные приемы, ведущие к решению исходной оптимальной задачи. [c.139]

Основная идея в применении метода неопределенных .пюжителей для оптимизации рассмотренного выше многостадийною процесса состоит в том, что при решении задачи оптимизации соотношения (IV,90), характеризующие связь входных н выходных параметров и управляющих воздействий на всех стадиях процесса, принимаются как ограничивающие условия, имеющие вид равенств, наложенные на переменные процесса часть из которых входит в выражение критерия оптимальности (IV,88). Это, в свою очередь позволяет использовать для решения оптимальной задачи математический аппарат метода неопределенных множителей Лагранжа (см стр. 139). [c.155]

Именно в этом п состоят нанболсе слабые стороны метода неопределенных множителе Лагранжа нрн е10 использовании для решения оптимальных задач, так как этот метод всегда дает лишь т.еобходпмые, но еще недостаточные условия о1ттпмальности. Более того, как показано ниже (см. главу VII), для целого ряда задач оитимальпые условия вообще нельзя найти при применении выражений (IV,216). [c.181]

Эти же результаты были получены выше при примеиеиии метода неопределенных множителей Лагранжа (сгр. 168). [c.275]

При т=1 задача не нмеет решения при т> (рис. 3.7) это задача на условный экстремум, которая может быть решена, на зрнмер, методом неопределенных множителей Лагранжа. Так [c.189]

Метод максимального элемента имеет преимущества по сравнению с другими методами оптимизации, применяемыми для определения оптимального состава резерва ХТС (например, метод неопределенных множителей Лагранжа, градиентный метод и др.), так как позволяет декомпозировать задачу поиска опти- [c.228]

Функция желательности. Задачу оптимизации процессов, ха-ракгеризующихся несколькими откликами, обычно сводят к задаче оптимизации по одному критерию с ограничениями в виде равенств или неравенств. В зависимости от вида поверхности отклика и ха-ракгера ограничений для оптимизации предлагается использовать методы неопределенных множителей Лагранжа, линейного и нелинейного программирования, ридж-анализ [10] и др. К недостаткам этих способов решения задачи оптимизации следует отнести вычислительные трудности. В частности, при описании поверхности отклика полиномами второго порядка решение задачи на условный экстремум с применением неопределенных множителей Лагранжа приводит к необходимости решать систему нелинейных уравнений. Поэтому одним из наиболее удачных способов решения задачи оптимизации процессов с большим количеством откликов является использование предложенной Харрингтоном [23] в качестве обобщенного критерия оптимизации так называемой обобщенной функции желательности О. Для построения обобщенной функции желательности О предлагается преобразовать измеренные значения от- [c.207]

В зависимости от способа минимизации штрафных функций МАВ или МП вычислительные методы идентификации делятся на две группы прямые и косвенные. Первую группу составляют методы непосредственной минимизации штрафной функции на каждом шаге интервала наблюдения. К ним относится градиентный метод и его многочисленные модификации, метод стохастической аппроксимации и др. Второй подход к решению задачи идентификации состоит в применении принципов теории оптимального управления на каждом шаге итерации. В частности, для минимизации штрафных функций применяется принцип максимума Понтрягина, метод неопределенных множителей Лагранжа и др. При этом соответствуюш ая система канонических уравнений с необходимыми граничными условиями образует характерную нелинейную двухточечную (начало и конец интервала наблюдения) краевую задачу (ДТКЗ), решение которой представляет искомую оценку для заданного интервала наблюдения. Вычислительные методы решения указанной ДТКЗ образуют группу так называемых непрямых вычислительных методов решения задач идентификации. К ним можно отнести метод квазилинеаризации, метод инвариантного погружения, метод прогонки и др. [c.494]

В настоящее время отсутствует общепринятая классифика-пия методов поиска экстремума нелинейной функции многих переменных. Обычно в качестве отдельной группы выделяют методы, разработанные в классической математике метод поиска оптимума путем решения системы нелинейных уравнений, полученных при приравнивании нулю частных производных исследуемой функции по оптимизируемым параметрам, и метод неопределенных множителей Лагранжа. Эти методы позволяют решать задачи поиска оптимума нелинейной функции многих переменных только при отсутствии ограничений на оптимизируемые параметры или при ограничениях в виде равенств. Поэтому указанные методы нельзя относить к методам нелинейного математического программирования. [c.121]

chem21.info

Динамическое программирование и Лагранжа метод множителе

В простейших случаях, когда целевая функция задана аналитически, используют классические методы нахождения экстремума методами дифференциального исчисления. При наличии ограничений типа равенств, наложенных на независимые переменные, используют метод множителей Лагранжа. В более сложных случаях, когда критерий оптимальности представлен в виде функционалов, используют методы вариационного исчисления-, при оптимизации процессов, описываемых системами дифференциальных уравнений, применяют принцип максимума Понтрягина. Используют также динамическое, линейное программирование и другие методы оптимизации. [c.38] Модификацией метода простого перебора является метод динамического программирования, сущность которого изложена в разделе 8.2.4. Показано [231, 237], что этот метод чрезвычайно точен, поскольку его применение позволяет рассматривать все возможные решения. Однако к недостаткам указанного метода следует отнести то, что он весьма трудоемок и требует большого объема памяти ЭВМ. В связи с этим рекомендуют [237] комбинировать менее точные, но более простые методы неопределенных множителей Лагранжа и наискорейшего спуска с методом динамического программирования при получении нецелочисленного решения для оптимального вектора состава поэлементного резерва— применять метод неопределенных мно- кителей Лагранжа, при получении целочисленного решения из нецелочисленного округлением — воспользоваться методом динамического программирования. [c.207]

В настоящее время для решения оптимальных задач применяют в основном следующие методы 1) исследование функций классического анализа 2) метод множителей Лагранжа 3) вариационное исчисление 4) динамическое программирование 5) принцип максимума 6) линейное программирование. Однако общего метода, пригодного для решения всех без исключения задач, возникающих на практике, нет. Вместе с тем каждый из перечисленных выше методов имеет предпочтительные области применения. Так, метод динамического программирования наилучшим образом приспособлен для решения задач оптимизации многостадийных процессов. Такие задачи чаще всего возникают при проектировании процессов ООС и СК, осуществляемых либо в многоступенчатых реакторах, либо в каскадах реакторов. Поэтому мы в сжатой форме рассмотрим основные положения метода динамического программирования. [c.191]

Следует также отметить, что множители Лагранжа часто применяют и в других методах оптимизации в качестве вспомогательного средства, позволяющего упростить решение более сложных задач (подробно см. главы, посвященные изложению вариационного исчисления и динамического программирования). [c.139]

Для решения задачи I уровня оптимизации—для определения оптимального варианта поэлементного резервирования — используется метод неопределенных множителей Лагранжа, отличающийся от других возможных методов (наискорейшего спуска, динамического программирования и других) сравнительной простотой реализации на ЭВМ. Для решения задачи II уровня оптимизации— выбора оптимальной величины надежности БТС — применяется метод сканирования по ряду предварительно задаваемых значений надежности системы. Математической моделью, устанавливающей влияние изменений в технологической топологии БТС за счет ввода резервных элементов на величину ее надежности, является параметрический граф надежности (п. г. н.) [c.174]

В настоящее время для решения оптимальных задач применяют в основном следующие методы 1) методы исследования функций классического анализа 2) методы, основанные на использовании неопределенных множителей Лагранжа 3) вариационное исчисление 4) динамическое программирование 5) принцип максимума 6) линейное программирование 7) нелинейное программирование. В последнее время разработан и успешно применяется для решения определенного класса задач метод геометрического программирования (см. главу X). [c.29]

Множители Лагранжа можно применять для решения задач оптимизации объектов с распределенными параметрами и задач динамической оптимизации. Область действия метода значительно расширяется за счет использования множителей Лагранжа в качестве вспомогательного средства, позволяющего упростить решение более сложных задач (например, в вариационном исчислении, динамическом программировании). [c.247]

Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их [c.31]

Нужно учитывать, что использование множителей Лагранжа в динамическом программировании не всегда позволяет найти решение оптимальной задачи, т. е. не всегда удается так выбрать значение множителя, чтобы выполнялось условие (VI, 60). Получить какие-либо общие условия возможности применения этого метода в достаточно компактной и удобной для проверки форме довольно трудно. Поэтому при практических расчетах вопрос о применимости множителей Лагранжа для конкретной задачи обычно решается методом проб. [c.282]

Таким образом, показано, что результаты, получаемые при применении метода множителей Лагранжа, вариационного исчисления и динамического программирования, можно представить в форме условий принципа максимума. Вместе с тем, соотношения принципа максимума, найденные независимо от этих методов, имеют более общий характер и позволяют решать задачи, которые не могут быть сформулированы в терминах этих методов или требуют специального обоснования возможности их применения. [c.404]

Каждое ограничение добавляет еще одно уравнение и на каждое ограничение вводится один множитель Лагранжа. Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе программирования, где с их. помощью иногда удается снизить размерность, решаемой задачи. [c.144]

Как отмечалось, весьма эффективен расчет по методу динамического программирования с разрывом обратной связи. При этом уравнения связи (П1, 113) используются как ограничения. Применяя метод неопределенных множителей Лагранжа, составляют новую целевую функцию [c.76]

Расчет производится по методу динамического программирования для различных значений неопределенного множителя Лагранжа Я. В результате получают Ф (А.), Хо Ск), Xi %) и т. д., а затем выбирают такое Я, при котором удовлетворяется уравнение связи [c.76]

Для решения этой задачи может быть использован метод динамического программирования или (при условии выпуклости функции Ф) метод неопределенных множителей Лагранжа. [c.159]

Значение суммарной нагрузки хо вводится в устройство либо автоматически непрерывно, либо периодически оператором. В зависимости от вида характеристик агрегатов в вычислительном устройстве могут применяться различные алгоритмы оптимального распределения, основанные на динамическом программировании, методе неопределенных множителей Лагранжа или градиентном методе. В первом случае вычислительное устройство должно представлять собой цифровую вычислительную машину (ЦВМ), во втором и третьем случаях могут быть применены ЦВМ или специализированные аналоговые машины АВМ. Остановимся подробнее на возможностях технической реализации оптимального распределения в зависимости от вида характеристик агрегатов. [c.182]

Наличие ограничений усложняет задачу оптимизации, для ее решения используют более сложные и трудоемкие методы, в том числе метод прямого перебора метод неопределенных множителей Лагранжа градиентные методы (наискорейшего спуска) максимального элемента, динамического программирования, ветвей и границ и др. [c.773]

Задача распределения п сортов хлора по потребителям с учетом указанных ограничений и критерия оптимизации (прибыли) решается методом динамического программирования. Для понижения размерности используется метод неопределенных множителей Лагранжа. [c.88]

Рассматриваемая система считается отказавшей, если в момент отказа работающего элемента -го типа все 5 запасных элементов этого же типа находятся в ремонте. Поставленная задача может решаться двумя способами. Первый из них является параметрическим обобщением метода множителей Лагранжа на случай дискретных переменных 143]. Второй основан на применении метода динамического программирования 130]. Второй способ более общий, может применяться при наличии нескольких линейных ограничений, полностью формализуется и дает приемлемую точность результатов. Наличие этих факторов позволяет применять модель определения оптимального уровня запасов резервных элементов на химических предприятиях различных типов, поэтому выбираем метод решения задачи, основанный на принципах динамического программирования. [c.100]

К каждой задаче с изопериметрическими ограничениями можно обычным способом применить метод динамического программирования. Существо этого метода будет рассмотрено в разд. 19 гл. 5 в связи с методом множителей Лагранжа. [c.163]

Из этого примера видно, что с помощью дифференциальных уравнений и множителей Лагранжа действительно можно решать такие задачи. Вопросы, связанные с возможными трудностями при решении уравнений для различных комбинаций т] и должны быть рассмотрены другими приемами. Именно в связи с этим динамическое программирование оказывается более простым методом. Вместо того чтобы совместно решать большое число уравнений, с помощью динамического программирования можно свести задачу к рассмотрению последовательности функций, зависящих лишь от одной из переменных, описывающих концентрации (см. разд. 2 гл. 3). В методе, использующем дифференциальные уравнения, каждому ограничению соответствуют два уравнения одно—для ограничения, другое—для связанного с ним множителя Лагранжа. В методе динамического программирования каждое ограничение сужает допустимую область и в сущности облегчает решение задачи. [c.199]

Множитель Лагранжа используется в обычных расчетах и вариационном исчислении при решении задач, содержащих ограничения. Его можно применять для решения таких задач также и в динамическом программировании. В динамическом программировании типичной задачей, где можно применить этот метод, является задача, в которой фиксированная величина ресурсов должна быть израсходована за N стадий. [c.218]

Вычислить fk Z) с помощью метода динамического программирования, линейного программирования и с помощью метода множителя Лагранжа. [c.269]

Как правило, нельзя рекомендовать какой-либо один метод, который можно использовать для решения всех без исключения задач, возникающих на практике. Одни методы в этом отношении являются более общими, другие — менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, нелинейное программирование) иа определенных этапах реикния оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием и принципом максимума. [c.29]

Препятствием для использования, например, метода неопределенных множителей Лагранжа является наличие ограничений на управляющие воздействия или переменные состояния в форме неравенств. С этим же препятствием приходится сталкиваться при использовании вариационного исчисления, когда в случае ограничений типа неравенств невозможно записать уравнения Эйлера. Наконец, при выводе уравнения Беллмана в динамическом программировании (VI, 146) необходимо допущение о дифференцируе-мости функции /, для которой записывается это уравнение и которая связана с критерием оптимальности процесса, заданным в виде функционала (VII, 545) соотношением [c.404]

chem21.info

Метод неопределенных множителей Лагранжа

Дом Метод неопределенных множителей Лагранжа
просмотров - 73

Для решения оптимизационных задач по методу Лагранжа параметры режима сети должны быть разделены на независимые переменные Yи зависимые переменные X,гдеY иX –векторы переменных.

Пусть общее количество параметров режима равно m, а число независимых параметров n.

Тогда число компонент вектора Х будет равно m-n.

При решении этим методом целевая функция оптимизации выражается как функция независимых переменных: Z = F(Y).

Кроме этого должны быть составлены ограничения в виде равенств, связывающих между собой независимые и зависимые переменные. Количество ограничений должно быть равно числу зависимых переменных.

К примеру, если общее количество параметров равно 5, из которых лишь 2 являются независимыми, то число ограничений должно быть равно трем:

w1(X,Y) = 0;

w2(X,Y) = 0;

w3(X,Y) = 0.

На следующем этапе находится функция Лагранжа, которая включает в себя и

целевую функцию и уравнения связи:

L = F(Y) + l1 × w1(X,Y) + l2 × w2(X,Y) + l3 × w3(X,Y),

где l1, l2 , l3 - неопределенные множители Лагранжа.

Далее крайне важно найти частные производные, число которых должно быть равно общему числу параметров:

¶L / ¶y1; ¶L / ¶y2; ¶L / ¶l1; ¶L / ¶l2; ¶L / ¶l3.

Приравнивая каждую из полученных частных производных нулю, получают систему уравнений, метод решения которых зависит от конкретного содержания задачи.

Пример 7. Найти экстремум функции Z = x1×x2 + x2×x3 при ограничениях

x1 + x2 = 2,

x2 + x3 = 2.

Р е ш е н и е.

Составляем функцию Лагранжа:

L = x1×x2 + x2×x3 + l1(x1 + x2 - 2) + l2(x2 + x3 - 2).

Дифференцируем её по переменным x1, x2, x3, l1, l2 и полученные выражения приравниваем нулю:

l1 + x2 = 0,

x1 + x3 + l1 + l2 = 0,

x2 + l2 = 0,

x1 + x2 - 2 = 0,

x2 + x3 - 2.

Из первого и третьего уравнений следует, что l1 = l2 = -x2.

По этой причине

x1 – 2x2 + x3 = 0,

x1 + x2 = 2,

x2 + x3 = 3,

откуда x1 = x2 = x3 =1. Экстремум целевой функции Zextr.= 2.

Поскольку, к примеру, точка (0; 2; 0) принадлежит допустимой области и в

ней Z = 0, то делаем вывод, что точка (1; 1; 1) – точка глобального максимума.

Open Library - открытая библиотека учебной информации. Оптимизация методом неопределенных множителей лагранжа

1.-2. Постановка задачи

Метод неопределенных множителей Лагранжа

2. Геометрическая интерпретация метода множителей Лагранжа

1.4 Метод неопределенных множителей Лагранжа

1.4.1 Основные положения

1.4.2 Геометрическая интерпретация метода множителей Лагранжа

3. Экономическая трактовка метода множителей Лагранжа

4. Численные методы решения задач нелинейного программирования

Метод "золотого сечения"

Метод неопределенных множителей Лагранжа

Неопределенный множитель Лагранж - Справочник химика 21

Динамическое программирование и Лагранжа метод множителе

Метод неопределенных множителей Лагранжа

Дом Метод неопределенных множителей Лагранжа просмотров - 73

Читайте также

Дом Метод неопределенных множителей Лагранжа
просмотров - 73