Математика 2 семестр / Математика 2 семестр / Оптимизация функции. Оптимизация функции
ОПТИМИЗАЦИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ — КиберПедия
В данной работе приводятся фундаментальные понятия и конкретные методы, используемые при поиске безусловных минимумов функций нескольких переменных.
Методы прямого поиска
Многомерные методы, реализующие процедуру поиска оптимума на основе вычисления значений функции, с общих позиций можно разделить на эвристические и теоретические. Эвристические методы, как это следует из названия, реализуют процедуры поиска с помощью интуитивных геометрических представлений и обеспечивают получение частных эмпирических результатов. С другой стороны, теоретические методы основаны на фундаментальных математических теоремах и обладают такими операционными свойствами, как сходимость (по крайней мере при выполнении некоторых определенных условий). Ниже рассматриваются три метода прямого поиска:
1) поиск по симплексу, или S2-метод;
2) метод поиска Хука — Дживса;
3) метод сопряженных направлений Пауэлла.
Первые два из перечисленных методов относятся к категории эвристических и реализуют принципиально различающиеся стратегии поиска. В процессе поиска по S2-методу последовательно оперируют регулярными симплексами в пространстве управляемых переменных, тогда как при реализации метода Хука— Дживса используется фиксированное множество (координатных) направлений, выбираемых рекурсивным способом. Метод Пауэлла основан на теоретических результатах и ориентирован на решение задач с квадратичными целевыми функциями; для таких задач метод сходится за конечное число итераций. К числу общих особенностей всех трех методов следует отнести относительную простоту соответствующих вычислительных процедур, которые легко реализуются и быстро корректируются.
Критерий оптимальности
Сначала рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условия, которые (в достаточно общих возможных ситуациях) позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли эти точки точками минимума, максимума или седловыми точками. При этом задача выбора указанных точек остаётся вне рамок проводимого анализа; основное внимание уделяется решению вопроса о том, соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется
минимизировать f(х), xÎRN, (3.1)
при отсутствии ограничений на х, где х — вектор управляемых переменных размерности N, f — скалярная целевая функция. Обычно предполагается, что xi(для всех значений i = 1, 2, 3,…, N)могут принимать любые значения, хотя в ряде практических приложений область значений х выбирается в виде дискретного множества. Кроме того, часто оказывается удобным предполагать, что функция f и ее производные существуют и непрерывны всюду, хотя известно, что оптимумы могут достигаться в точках разрыва f или ее градиента
(3.2)
Функция f может принимать минимальное значение в точке , в которой f или f претерпевают разрыв. Кроме того, в этой точке f может не существовать. Для того чтобы построить систему конструктивных критериев оптимальности, необходимо (по крайней мере на первой стадии исследования) исключить из рассмотрения подобные ситуации, которые весьма усложняют анализ. Наконец, в ряде случаев приходится ограничиваться лишь идентификацией локальных оптимумов, поскольку нелинейная целевая функция f не всегда обладает свойством выпуклости и, следовательно, может оказаться мультимодальной.
Далее перейдем к вопросу анализа «в динамике», который формулируется следующим образом: если точка х(0)не удовлетворяет условиям, налагаемым упомянутыми выше критериями оптимальности, то как получить «хорошее» новое приближение x(1)к решению х*? Попытка дать ответ на этот вопрос приводит к необходимости рассмотрения ряда методов, описание которых составляет значительную часть данной главы. Рассматриваемые методы классифицируются в соответствии с тем, используется ли информация о производных исследуемых функций.
Рассматрим условия, которые позволяют характеризовать (т. е. классифицировать) точки пространства управляемых переменных. Критерии оптимальности необходимы для распознавания решений и, кроме того, составляют основу большинства используемых методов поиска решений. Рассмотрим разложение Тейлора для функции нескольких переменных:
f(x)=f( )+ f( ) ∆x+½∆x f( )∆x+O (∆x), (3.3)
где — точка разложения из пространства RN; ∆х = х - — величина изменения х; f(x) — N-мерный вектор-столбец первых производных f(х), вычисленных в точке ; f( ) = H ( ) — симметрическая матрица порядка N×N вторых частных производных f(x), вычисленных в точке . (Эту матрицу часто называют матрицей Гессе. Ее элемент, расположенный на пересечении i-й строки и j-го столбца, равен f / dx x .) O (∆x) — сумма всех членов разложения, имеющих порядок по ∆x выше второго. Пренебрегая членами высших порядков (т. е. исключая O (∆x)), определим величину изменения целевой функции f(х), соответствующего произвольному изменению х:
∆ f(x)= f(x) - f( ) = f( ) ∆x+½∆x f( )∆x (3.4)
Напомним, что по определению во всех точках из окрестности точки минимума целевая функция принимает значения, которые превышают минимальное, т. е. имеет место неравенство
∆f = f(x) - f( ) ≥0. (3.5)
Точка является точкой глобального минимума, если неравенство (3.5) выполняется для всех хÎ RN; такие точки будем обозначать через х**. Когда формула (3.5) справедлива лишь в некоторой δ-окрестности точки , т. е. для всех х, таких, что ||х – || < δ при заданном δ > 0, то есть точка локального минимума, или х*. Если же
то есть точка максимума (локального или глобального в соответствии с данными выше определениями). Исключение знака равенства из формул (3.5) и (3.6) позволяет определить точку строгого минимума или максимума. В случае когда ∆f принимает как положительные и отрицательные, так и нулевые значения в зависимости от выбора точек из δ-окрестности, точка представляет собой седловую точку.
Вернемся к равенству (3.4) и вспомним о выдвинутом ранее предположении о том, что f(х), f(x) и f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент f( ) должен быть равен нулю, т. е. должна быть стационарной точкой. В противном случае разность ∆f может принимать положительные или отрицательные значения в зависимости от знаков f( ) и ∆х. Таким образом, точка должна удовлетворять условию стационарности
f( ) = 0, (3.7)
и формула (3.4) принимает следующий вид:
∆f(x) = +½∆x f( )∆x. (3.8)
Очевидно, что знак ∆f(x) определяется квадратичной формой
Q(х) = ∆x f( )∆x (3.9)
или Q(z)=zTAz.
Из линейной алгебры известно, что
А — положительно полуопределенная матрица, если Q (z)≥0 для любых z;
А — отрицательно определенная матрица, если Q(z)<0 для любых z; (3.10)
А — отрицательно полуопределенная матрица, если Q(z)≤0 для любых z;
А — неопределенная матрица, если Q (z)>0 для некоторых z и Q(z)<0 для остальных z.
Из (3.10) следует, что стационарная точка есть
точка минимума, если 2f( ) — положительно полуопределенная матрица;
точка максимума, если 2f( ) — отрицательно полуопределенная матрица; (3.11)
cедловая точка, если 2f(x) 0 — неопределенная матрица.
2.3 Метод поиска по симплексу (S2-метод)
Первые попытки решения оптимизационных задач без ограничений на основе прямого поиска связаны с использованием одномерных методов оптимизации. Как правило, при реализации таких методов допустимая область определения показателя качества функционирования системы (целевой функции) заменяется дискретным множеством (решеткой) точек пространства управляемых переменных, а затем используются различные стратегии уменьшения области, которая содержит решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах решетки и, следовательно, непригодной для решения задач с числом переменных, превышающим 2. Более полезная идея заключается в выборе базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с двумя переменными можно воспользоваться квадратным образцом, изображенным на рис. 3.1. Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится, аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Рисунок 3.1 - Квадратный образец (частный случай кубического образца)
Этот тип эволюционной оптимизации был использован Боксом и другими исследователями для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба, т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно N, то поиск по кубическому образцу требует 2 +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.
Одна из вызывающих особый интерес стратегий поиска положена в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер. Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в N-мерном пространстве представляет собой многогранник, образованный N+1 равностоящими друг от друга точками-вершинами.
Например, в случае двух переменных симплексом является равносторонний треугольник; в трехмерном пространстве симплекс представляет собой тетраэдр. В алгоритме симплексного поиска используется важное свойство симплексов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается. Нетрудно видеть, что при переходе к новому симплексу требуется одно вычисление значения целевой функции. Рис. 3.2 иллюстрирует процесс построения нового симплекса на плоскости.
a — начальный симплекс; x(1), x(2), x(3); б — новый симплекс; x(2),x(3), x(4)
Рисунок 3.2 - Построение нового симплекса
Алгоритм симплекс-метода
Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом определяется вершина, которой соответствует наибольшее значение целевой функции. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка минимума, либо не начнется циклическое движение по двум или более симплексам. В таких ситуациях можно воспользоваться следующими тремя правилами.
cyberpedia.su
Оптимизация функции
Задание: ОПТИМИЗАЦИЯ ФУНКЦИИ
Оптимальные значения функции f (x, y) на некотором множествеD ‒ ее наибольшееfнаиб. fMAX и наименьшееfнаим. fMIN значения (заглавные латинские буквы подразумевают "глобальный" максимум и минимум, в отличие от локальных, которые будем обозначать строчными буквами ‒fmax иfmin ). Оптимальные точки функции ‒ точки, в которых функция принимает
оптимальные значения. Задача оптимизации функции состоит в нахождении ее оптимальных значений и оптимальных точек. Естественно, имеется две задачи оптимизации ‒ поиск наибольшего
значения и поиск наименьшего значения. Решение задачи оптимизации ‒ пара fOPT , ARGOPT
из оптимального значения fOPT и набораARGOPT оптимальных точек, в которых функция принимает это значение. Если множествоD компактно, а функцияf непрерывна, то обе задачи оп-
тимизации имеют решение (теорема Вейерштрасса). Если оптимальное значение принимается в единственной точке, то говорят, что решение единственное. Ситуацию, когда оптимальное значение принимается в нескольких точках, называют "альтернативным оптимумом".
Пример 1. Пусть f (x) sin x ,D ( ; ) . ТогдаfMAX 1,ARGMAX / 2 2 k, k Z ,fMIN 1,ARGMIN / 2 2 k, k Z .
Пример 2. Пусть f (x) sin x ,D (0; ) . ТогдаfMAX 1,ARGMAX / 2 , наименьшего значения в данном случае нет (почему?).
Домашнее задание состоит из двух частей ‒ исследование критических (в данном случае, стационарных) точек функции в области ее определения и задача оптимизации функции в указанной области.
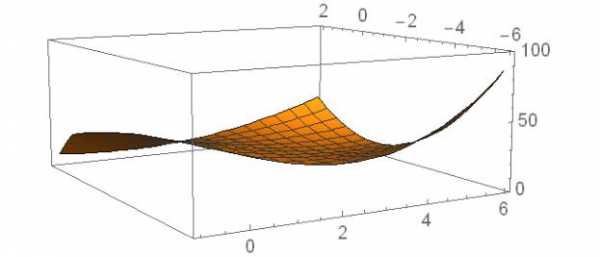
1. Найти и исследовать критические точки функции f (x, y) ( y 1)2 (x 3) (x 5)2 10.
Решение. Область определения функции ‒ R2 (вся плоскость). Находим точки стационарности функции ‒ точки, в которыхgrad f (x, y) 0 , точки, в которыхвсе частные производные
равны нулю. Вычисляем f (x, y) ( y 1)2 | 2(x 5), | f (x, y) 2( y 1)(x 3) и решаем систему |
x |
| y |
| ( y 1)2 2(x 5) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
уравнений |
| . Получаем три стационарных точки (они же ‒ "подозритель- | ||||||||||||||||
| 2( y 1)(x 3) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
ные" на локальный экстремум): M1 (3; 3) ,M2 (3;1) | и M3 (5; 1). |
|
|
|
|
| ||||||||||||
Вычисляем вторые производные и записываем матрицу Гессе: | f (x,y) 2, | f (x,y) 2(x 3), | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| xx |
|
|
| yy |
|
| |
|
|
|
|
|
|
|
|
|
| (x,y) |
| (x,y) |
|
| 2 | 2( y 1) |
| |
f (x, y) | f | (x,y) 2(y 1). Матрица | H (x, y) | fxx | fxy |
| . | |||||||||||
| f | (x,y) | f | (x,y) | 2( y 1) 2(x 3) | |||||||||||||
xy | yx |
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
| yx |
| yy |
|
|
|
|
|
| |
Точка M1 (3; 3) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2 | 4 |
|
| 4 |
| 16 | 0 . Согласно признаку, в точкеM1 (3; 3) |
| ||||||||||
2 |
|
| ||||||||||||||||
H (M1 ) | 4 | , DetH (M1 ) | 4 | 0 |
|
| ||||||||||||
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
локального экстремума нет (седловая точка, точка гиперболического типа).
Точка M2 (3;1) : |
|
|
|
|
|
|
| |||
H (M2 ) | 2 | 4 |
| 2 ) |
| 4 |
| 16 | 0 . Согласно признаку, в точкеM2 (3;1) | локально- |
2 |
| |||||||||
|
| , DetH (M |
|
|
| |||||
| 4 | 0 |
|
| 4 | 0 |
|
|
|
|
го экстремума нет (седловая точка, точка гиперболического типа).
Точка M3 (5; 1) : |
|
|
|
|
|
|
|
|
| ||
2 | 0 |
| Det H (M3 ) |
| 0 |
| 8 | 0 . Согласно признаку, в точкеM3 (5; 1) |
| ||
2 |
|
| |||||||||
H (M3 ) | 4 | , | 0 | 4 |
| есть ло- | |||||
0 |
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| (M3 ) 2 | 0 , тоM3 (5; 1) ‒ точка | |
кальный экстремум (точка эллиптического типа). Так как fxx | |||||||||||
локального минимума. Значение f (M3 ) f (5; 1) 10 .
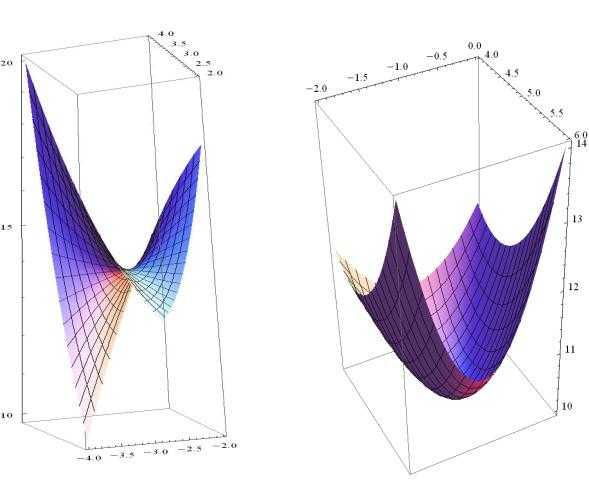
График в окрестности седловой точки | График в окрестности точки локального минимума |
2. Найти наибольшее fMAX и наименьшееfMIN значения этой функции в областиD , ограниченной линиямиy x ,y 2 ,x 1 иx 6 .
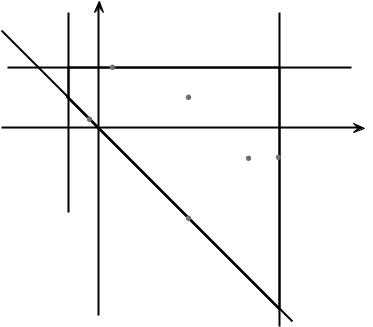
Рисуем область.
| y |
|
|
C | M4 | y 2 | B |
E | M6 | M2 |
|
x 1 | O |
| x |
|
|
| |
|
| M3 | M5 |
|
|
| |
|
| M1 | x 6 |
|
|
| |
|
| y x |
|
| 6 |
| A |
|
|
|
Получился четырехугольник (трапеция) ABCE .
Из общих соображений понятно, что оптимальные точки следует искать среди точек локальных экстремумов, лежащих внутри области, и среди точек на границе области. Маленькая хитрость состоит в том, что в задаче оптимизации, как правило, не проводят исследование критических точек на экстремум, ограничиваясь только вычислением значений функции.
Из первой части задания выписываем критические точки, попавшие вовнутрь области, и вычисляем значения функции: M2 (3;1) ,f (M2 ) 14 ;M3 (5; 1) ,f (M3 ) 10 .
Приступаем к исследованию функции на границе области (так называемая задача условной оптимизации ‒ найти оптимальные значения функции при условии, что ее аргумент находится на границе области). Граница состоит из четырех отрезков, поэтому придется четыре раза проделать примерно одно и то же.
Отрезок CB . Его уравнениеy 2 ,1 x 6 . ОбозначимfCB (x) функцию | f (x, y) при усло- | ||||
вии, что y 2 . В данном случаеf | CB | (x)f (x; 2) 9(x 3) (x 5)2 10 | x2 x 8 . Получаем | ||
|
|
|
|
| |
"школьную" задачу ‒ найти наибольшее и наименьшее значение функции | f | CB | (x)x2 x 8на | ||
отрезке [ 1; 6] .
Вычисляем производную, приравниваем ее к нулю, находим критические точки, попавшие вовнутрь отрезка, затем вычисляем значения функции в этих точках и на концах промежутка.
| (x) 2x 1 0 | x 0,5[1; 6]; | fCB 0,5 7, 75, | fCB 1 10, | fCB 6 38. |
fCB |
Возвращаемся к исследуемой функции. Вспоминаем, что на отрезке CB y 2 . В области определения возникает новая точкаM4 (0,5; 2) (отмечаем ее на рисунке) иf (M4 ) fCB (0,5) 7, 75 . Концы отрезка ‒ точкиC иB , поэтомуf (C) fCB (1) 10 ,f (B) fCB (6) 38 .
Отрезок AB . Его уравнениеx 6 ,6 y 2 . Обозначим | fAB ( y) функциюf (x, y) при усло- | |||||
вии, что x 6 . В данном случаеf | AB | ( y)f (6;y) 3(y 1)2 | 11. Получаем задачу ‒ найти | |||
|
|
|
|
|
| |
наибольшее и наименьшее значение функции f | AB | ( y) 3(y 1)2 11на отрезке [ 6; 2]. | ||||
|
|
|
|
|
| |
| y 1[6; 2]; fAB | 1 11, fAB 6 86, fAB 2 38. | ||||
fAB (y) 6(y 1) 0 | ||||||
Последнее значение можно было не вычислять (почему?). Разве что для контроля вычислений.
Возвращаемся к исследуемой функции. На отрезке AB x 6 . В области определения возникает новая точкаM5 (6; 1) иf (M5 ) fAB (1) 11. На концеA имеемf (A) fAB (6) 86 .
Отрезок CE . Его уравнениеx 1 ,1 y 2 . ОбозначимfCE ( y) функциюf (x, y) при условии,
что x 1. В данном случаеf | CE | ( y) f ( 1; y) 4( y 1)2 46 . Получаем задачу ‒ найти | |||
наибольшее и наименьшее значение функции f | CE | ( y) 4(y 1)2 | 46 на отрезке[1; 2] . | ||
|
|
|
|
| |
f ( y) 8( y 1) 0 y 1[1; 2], остается только вычислить значение функции на левом
CE
конце: fCE 1 20 .
Возвращаемся к исследуемой функции. На отрезке CE x 1 , поэтомуf (E) fCE (1) 20 .
Остался отрезок EA . Его уравнениеy x , | 1 x 6 . ОбозначимfEA (x) функциюf (x, y) | ||||||||||||||
при условии, что y x . В данном случае |
|
|
| ||||||||||||
f | EA | (x)f (x;x) (x 1)2 (x 3) (x 5)2 | 10 x3 4x2 3x 32 . Ищем наибольшее и | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
наименьшее значение функции |
|
| f | EA | (x)x3 | 4x2 | 3x 32на отрезке [ 1; 6]. | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
f |
| (x) 3x2 8x 3 0 | x |
| 1 | [ 1; 6], | x 3 [ 1; 6] . Очень редкое явление ‒ "хоро- | ||||||||
| |||||||||||||||
| EA |
|
|
|
| 1 |
|
| 3 |
|
| 2 | |||
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
| 1 |
| 878 |
|
|
| fEA 3 14 . Значения на концах можно не вычислять. | ||||||
шие корни". Далее fEA |
|
|
|
|
|
|
| 32,5 , | |||||||
|
|
|
|
| |||||||||||
|
|
| 3 |
|
|
| 27 |
|
|
|
|
|
| ||
Возвращаемся к исследуемой функции. Уравнение отрезка EA | y x . В области определения |
возникает новая точка M6 (1/ 3;1/ 3) и уже знакомая по из первой части точкаM1 (3; 3) . По- | |
следние вычисления: f (M6 )fEA (1/ 3) 878 / 27 32,5, а | f (M1)fEA (3) 14. |
Осталось "подведение итогов". Выписываем все отмеченные точки и значения функции в этих точках в таблицу (не обязательно):
f (M1)f (3; 3) 14 |
|
|
|
f (M2 )f (3;1) 14 |
|
|
|
f (M3 )f (5; 1) 10 |
|
|
|
f (M4 )f (0,5; 2) 7, 75 | MIN |
|
|
f (M5 )f (6; 1) 11 |
|
f (M6 )f ( 1/ 3;1/ 3) 32,5 |
|
f (A)f (6; 6) 86 | MAX |
|
|
f (B)f (6; 2) 38 |
|
|
|
f (C)f ( 1; 2) 10 |
|
|
|
f (E)f ( 1;1) 20 |
|
|
|
Остается записать ответ и посмотреть на картинку.
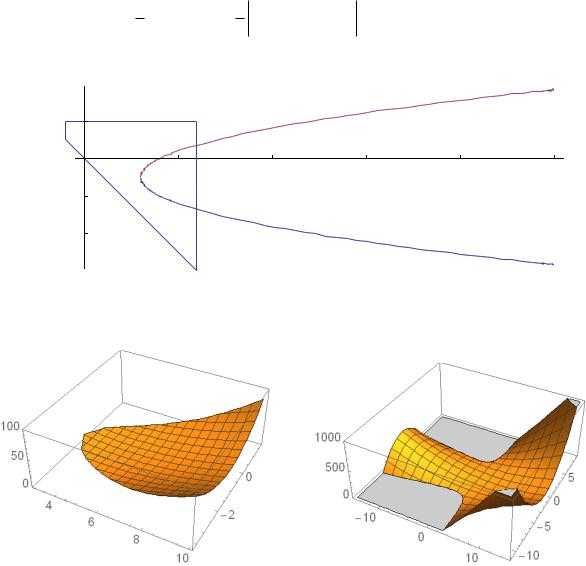
Дополнение. Множество точек, в которых определитель матрицы Гессе равняется нулю (точек па- | |||||
раболического типа) оказывается параболой, определяемой уравнением |
| ||||
1 DetH (x,y) | 1 | 2 | 2( y 1) x 3 (y 1)2 0. |
| |
4 | 4 2(y 1) | 2(x 3) |
|
| |
Парабола разбивает плоскость на две области |
|
|
| ||
2 |
|
|
|
|
|
5 |
| 10 | 15 | 20 | 25 |
2 |
|
|
|
|
|
4 |
|
|
|
|
|
Все точки вне параболы имеют гиперболический тип, а внутри ‒ эллиптический тип. Во внутрен- | |||||
ней области функция выпукла вниз, а все точки графика, расположенные над внешней областью ‒ | |||||
седловые. |
|
|
|
|
|
На поверхности графика лежит прямая линия, проходящая через точку (3; 0;14) , параллельная осиOy . Ее можно разглядеть на втором рисунке.
studfiles.net
Методы оптимизации функции одной переменной
Требуется найти безусловный минимум функции 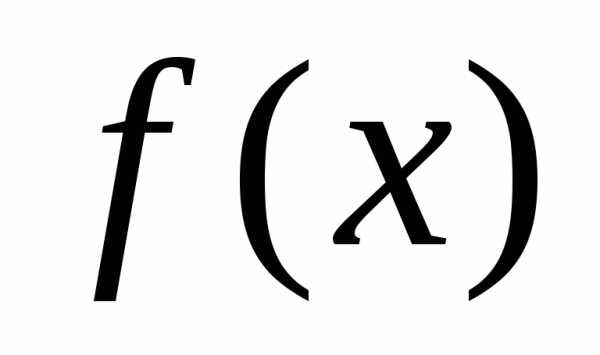 одной переменной, т.е. такую точку
одной переменной, т.е. такую точку , что.
, что.
Для решения этой задачи могут быть использованы методы полиномиальной аппроксимации, которые основываются на аппроксимации на некотором интервале 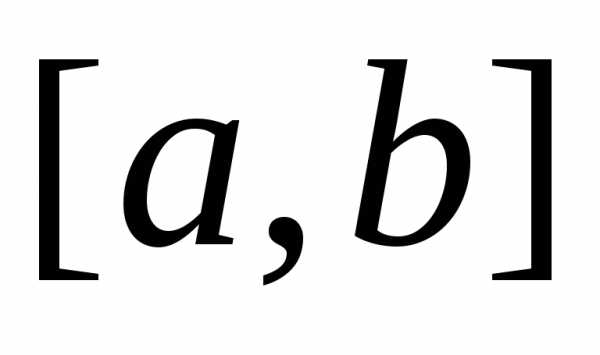 , таком, что
, таком, что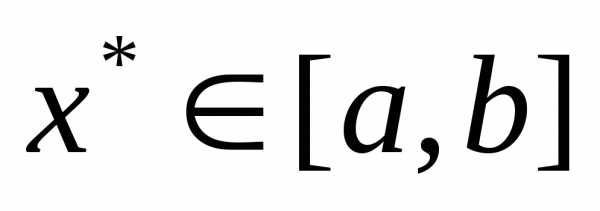 , функции
, функции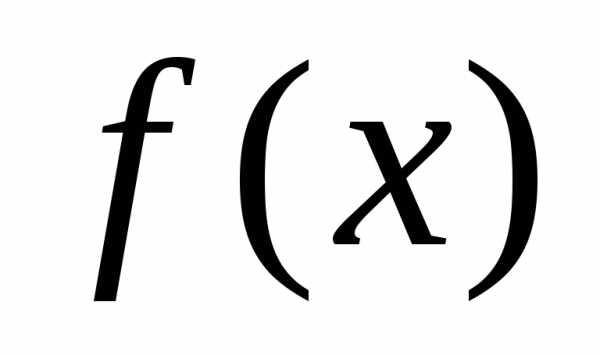 некоторым полиномом
некоторым полиномом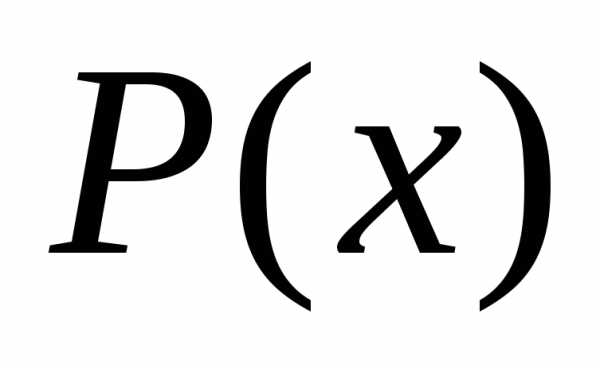 . Тогда задача нахождения минимума функции
. Тогда задача нахождения минимума функции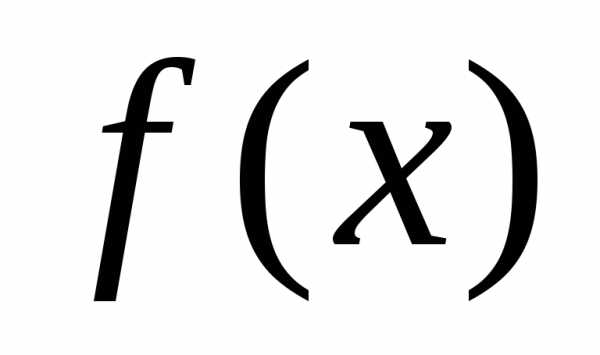 заменяется задачей нахождения минимума полинома
заменяется задачей нахождения минимума полинома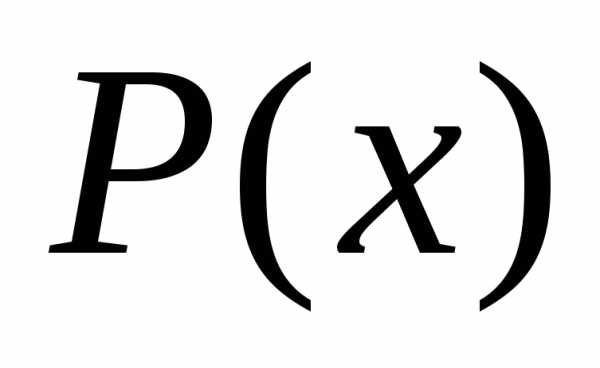 . Необходимыми условиями эффективной реализации такого подхода является унимодальность и непрерывность
. Необходимыми условиями эффективной реализации такого подхода является унимодальность и непрерывность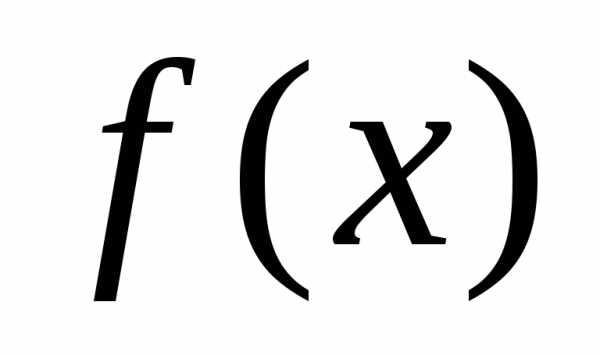 в аппроксимируемом интервале.
в аппроксимируемом интервале.
Согласно теореме Вейерштрасса об аппроксимации, если функция непрерывна в некотором интервале, то её с любой степенью точности можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно её аппроксимирует, то координату точки оптимума функции можно оценить координатой точки оптимума полинома.
Согласно теореме Вейерштрасса качество оценок координат точки оптимума можно повысить двумя способами:
использованием полинома более высокого порядка
уменьшением интервала аппроксимации.
Второй способ является более предпочтительным, поскольку процедура построения полинома выше 3-го порядка довольно сложная.
Метод квадратичной интерполяции
Пусть известно значение функции f(x) в трех несовпадающих точках х1, х2, х3. Тогдаf(x) может аппроксимирована квадратичным полиномом вида:
где A,B,C– определяются из уравнения:

После решения этих уравнений получаем:
A=[(x3-x2)f1+(x1-x3)f2+(x2-x1)f3]/
B=[(x22-x32)f1+(x32-x12)f2+(x12-x22)f3]/
C=[x2x3(x3-x2)f1+ x1x3 (x1-x3)f2+ x2x1 (x2-x1)f3]/
=(x1-x2)(x2-x3)(x3-x1)
Точка минимума полинома 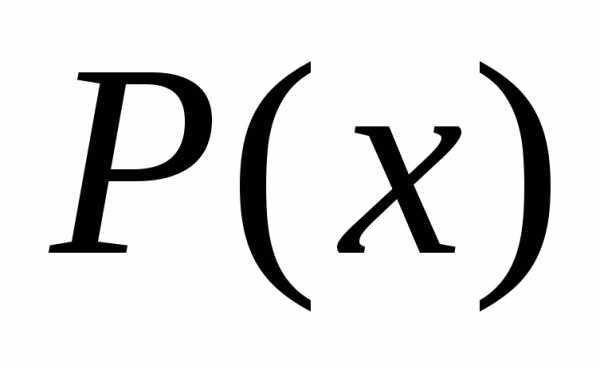 вычисляется следующим образом:
вычисляется следующим образом: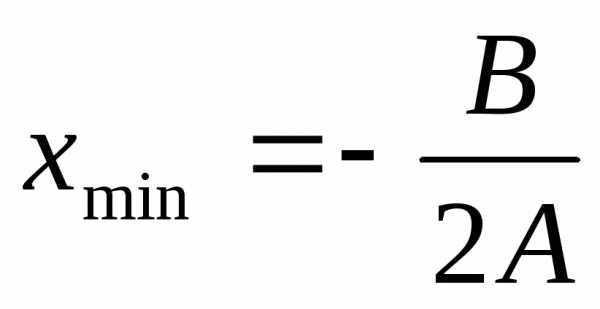 , при
, при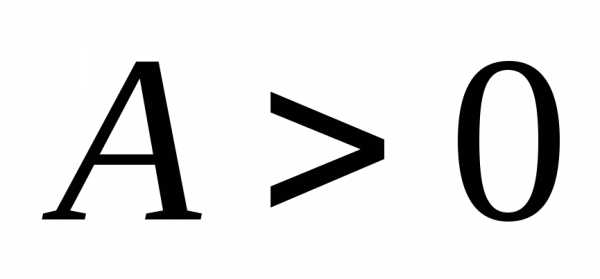
Тогда оценить точку оптимума функции f(x) можно значением (оценка оптимальности):
(оценка оптимальности):
Метод Пауэлла (квадратичной интерполяции)
Шаг1. Задать начальную точку 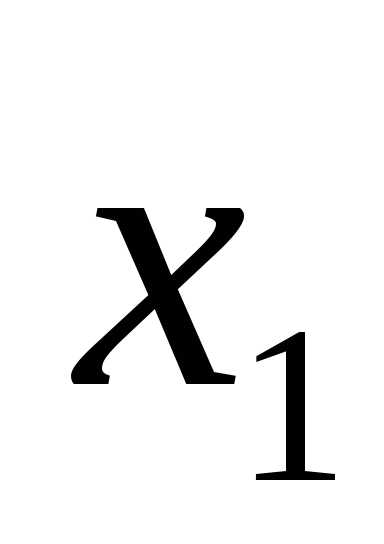 , величину шага
, величину шага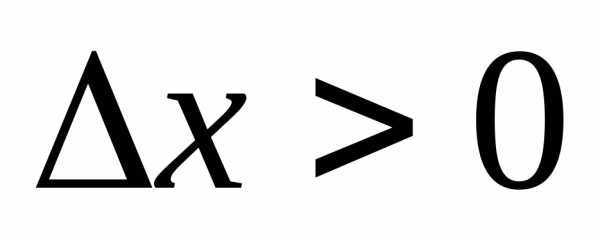 ,
,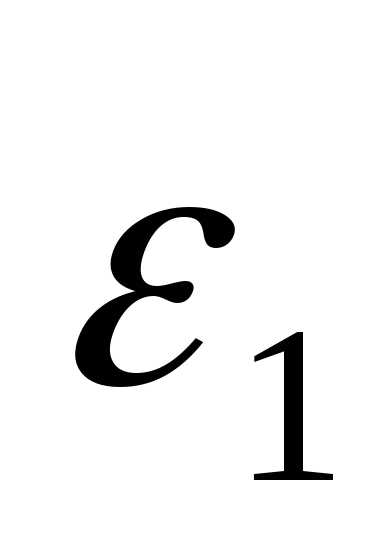 и
и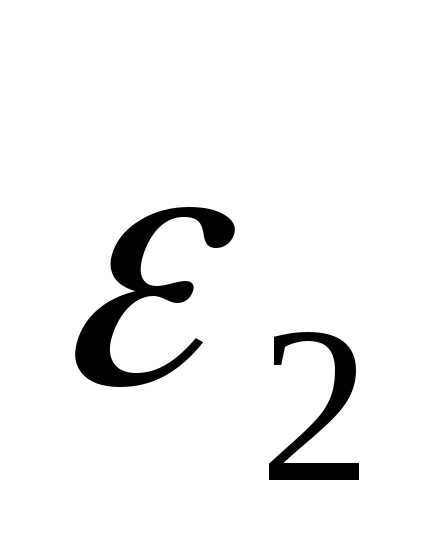 - малые положительные числа, характеризующие точность
- малые положительные числа, характеризующие точность
Шаг 2. Вычислить
Шаг 3. Вычислить и
Шаг 4. Сравнить 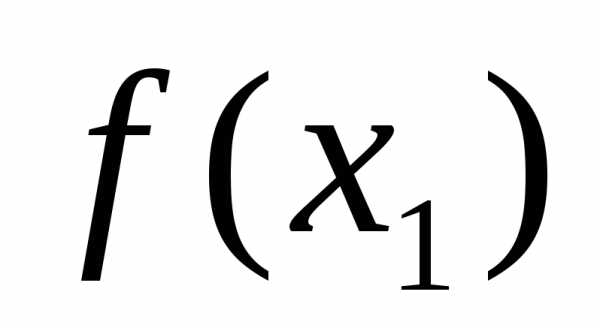 с
с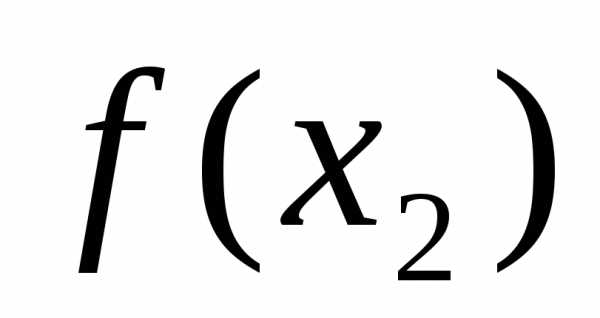 :
:
а) если , положить
б) если , положить
Шаг 5. Вычислить
Шаг 6. Найти ,
Шаг 7. Вычислить точку минимума интерполяционного полинома, построенного по трем точкам:
и величину функции 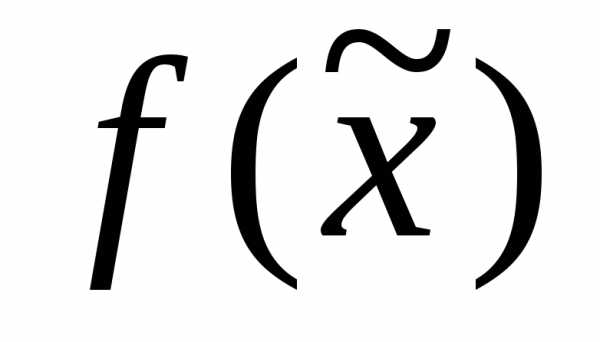 . Если знаменатель дроби на некоторой итерации обращается в ноль, то результатом интерполяции является прямая. В этом случае рекомендуется обозначить
. Если знаменатель дроби на некоторой итерации обращается в ноль, то результатом интерполяции является прямая. В этом случае рекомендуется обозначить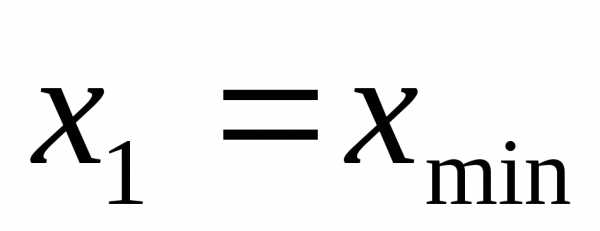 и перейти к шагу 2.
и перейти к шагу 2.
Шаг 8. Проверить выполнение условий окончания:
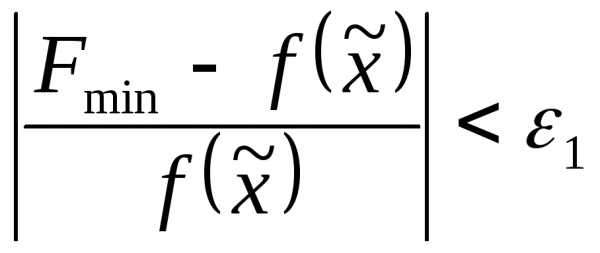 и
и 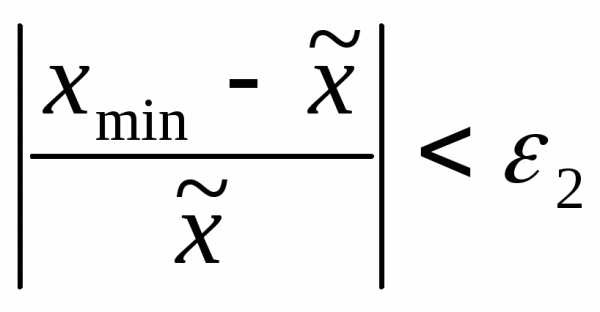 .
.
Тогда
а) если оба условия выполнены, процедура закончена и 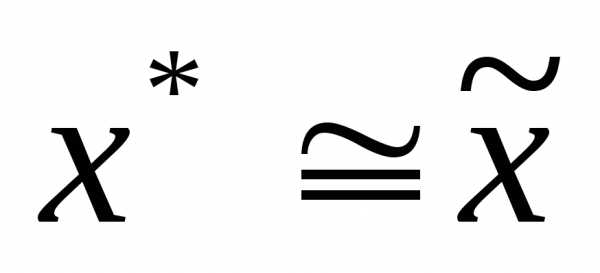 ;
;
б) если хотя бы одно из условий не выполнено и , выбрать наилучшую точку (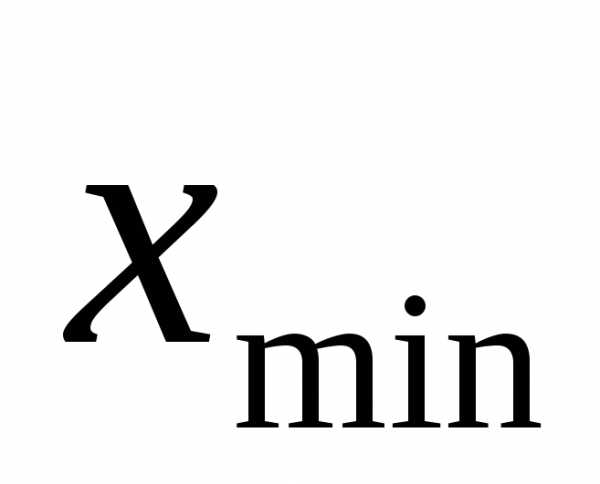 или
или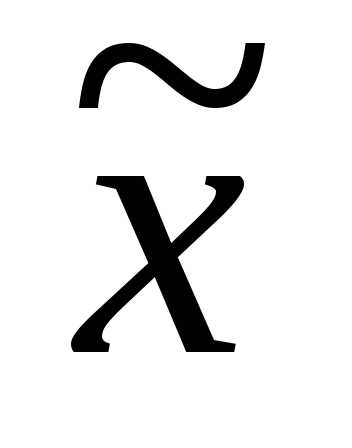 ) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 6.
) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 6.
в) если хотя бы одно из условий не выполнено и , то положить и перейти к шагу 2.
и перейти к шагу 2.
Метод первого приемлемого значения (квадратичная интерполяция с использованием производных).
Данный метод отличается от предыдущего тем, что полином строится исходя из значений f(x) в двух точках х1, х2 (f(х1) иf(х2)) иf’(х1) илиf’(х2) (производная определяет тангенс угла наклона в точке).
Тогда для нахождения коэффициентов квадратичного полинома 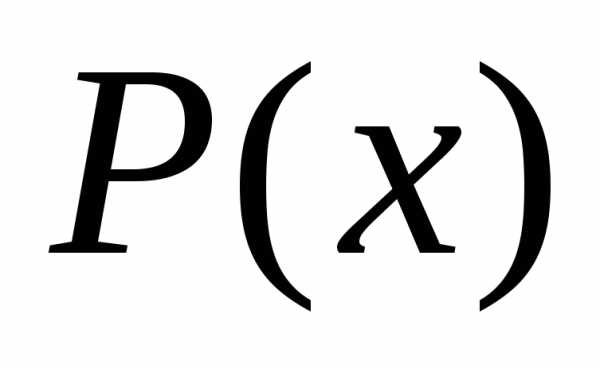 используется следующая система:
используется следующая система:
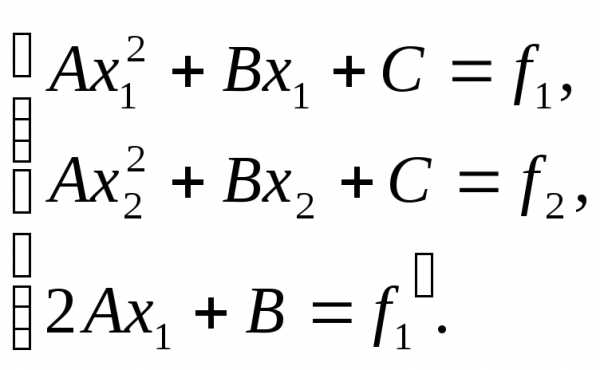
Решая эту систему получаем:
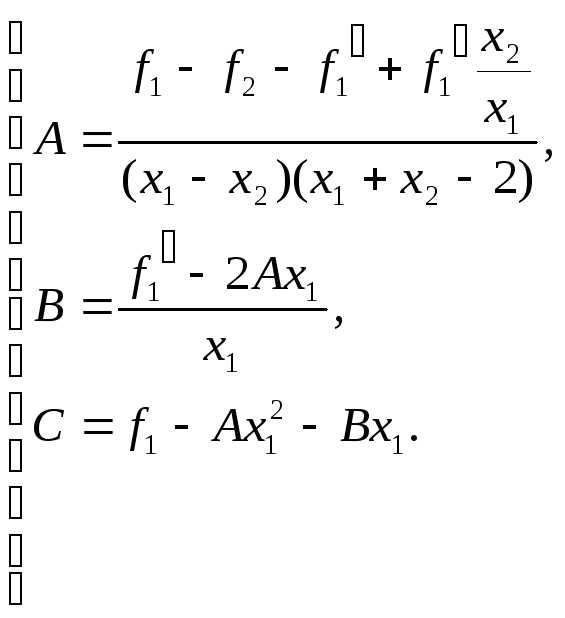
Метод кубической интерполяции (Давидона)
Для кубической интерполяции в методе Давидона используется значение функций и ее производных, вычисленных в точках х1, х2.
Используется кубический полином следующего вида:
Параметры а0, а1, а2, а3 подбираются т.о., чтобы значениеP(х) иP’(х) в точках х1, х2совпадали со значениямиf(х) иf’(х).
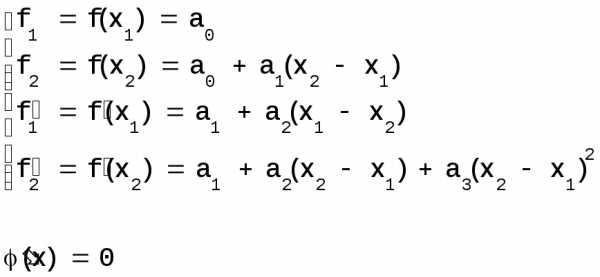
Решение, определяющее стационарную точку кубического полинома выглядит следующим образом:
Эта формула гарантирует, что точка  расположена между х1, х2.
расположена между х1, х2.
Процесс поиска заканчивается, если производная в полученной точке достаточно мала, или процедура становится неэффективной.
studfiles.net
Методы оптимизации функций многих переменных
Кафедра: ИТ
МЕТОДЫ ОПТИМИЗАЦИИ ФУНКЦИЙ
МНОГИХ ПЕРЕМЕННЫХ
Екатеринбург 2007
Оглавление
Введение
Лабораторная работа № 1.
1. Методы безусловной оптимизации
1.1 Теоретический обзор. Исследование функции на безусловный экстремум
1.2 Численные методы минимизации функции
2. Порядок выполнения лабораторной работы
3. Пример выполнения лабораторной работы
4. Задания для лабораторного практикума
Лабораторная работа № 2.
1. Методы условной оптимизации
1.1 Теоретический обзор. Решение задачи минимизации со смешанными ограничениями
1.2 Седловые точки функции Лагранжа
1.3 Решение задач квадратичного программирования методом седловой точки
2. Порядок выполнения лабораторной работы
3. Пример выполнения лабораторной работы
4. Задания для лабораторного практикума
Библиографический список
Приложение
Настоящая работа является первой в серии методических указаний к лабораторным работам по дисциплинам "Методы оптимизации и нелинейное программирование" и "Методы оптимизации". Данные дисциплины читаются студентам 2-го курса специальности 230101 - Вычислительные машины, комплексы, системы и сети и направления 230100 - Информатика и вычислительная техника (бакалавры).
В указаниях рассматриваются задачи безусловной и условной нелинейной оптимизации. В теоретической части по каждой теме приводятся базовые понятия, теоремы и алгоритмы, которые потребуются для выполнения работ. Для выполнения графической и расчетной частей задач и реализации численных методов оптимизации студенты должны применить знание языков программирования и пакетов MATLAB, MATCAD, EXCEL. Выбор конкретного инструмента предоставляется самому студенту. Приведены примеры порядка выполнения и оформления лабораторных работ.
Проведенные вычисления, графические работы, анализ полученных результатов должны быть оформлены в виде отчета в соответствии со стандартными требованиями, предъявляемыми к отчетам и пояснительным запискам [1]. Сведения из теории, содержащиеся в данных методических указаниях, в отчет включать не рекомендуется.
Цель лабораторной работы - закрепление навыков исследования функций на выпуклость, решение задач на нахождение безусловного экстремума выпуклой функции аналитически и численными методами, изучение способов визуализации функций двух переменных в EXCEL и MATLAB.
Рассматривается задача
f (x ) → extr, x
Rn . (1)Метод поиска безусловного экстремума основывается на следующих утверждениях:
Пусть функция f ( x) дифференцируема в точке х*
Rn . Тогда если х* - локальное решение задачи (1), тоgradf ( x* ) = 0. (2)
Пусть функция f (x ) дважды дифференцируема в точке х*
Rn . Тогдаа) если х* - точка локального минимума в задаче (1), то матрица Гессе Н (х* ) неотрицательно определена, т.е.
р Rn выполняется неравенство (Н (х* ) р,р ) ≥0;б) если х* - точка локального минимума в задаче (1), то матрица Н (х*) неположительно определена, т.е.
р Rn выполняется неравенство (Н (х* ) р,р) ≤0.Пусть функция f ( x) дважды дифференцируема в точке х*
Rn иgradf ( x* ) = 0. Тогда
а) если матрица Н (х* ) положительно определена, т.е.
р Rn , р ≠0, (Н (х* ) р,р) >0, то х* - точка строгого локального минимума функции f ( x) на Rn ;б) если матрица Н (х* ) отрицательно определена, т.е.
р R , р ≠0, (Н (х* ) р,р) х* - точка строгого локального максимума функции f ( x) на Rn .Если gradf ( x* ) = 0, то х* называется стационарной точкой. Для выпуклой (вогнутой) на Rn функции стационарные точки являются точками ее глобального минимума (максимума). Строго выпуклые (вогнутые) функции имеют единственный глобальный минимум (максимум).
Критерий выпуклости функции. Дважды непрерывно дифференцируемая на выпуклом множестве Х с непустой внутренностью функция является выпуклой (вогнутой) на этом множестве в том и только том случае, когда матрица Гессе Н (х* ) неотрицательно (не положительно) определена для всех х
Х .При исследовании на знакоопределенность матрицы вторых производных функции рекомендуется применять критерий Сильвестра или анализ собственных значений матрицы.
Схема поиска безусловных экстремумов функции:
Составить и решить систему алгебраических уравнений (2).
В стационарных точках (точках, являющихся решением системы (2)) исследовать на знакоопределенность матрицу вторых производных; точки, в которых Н (х) > 0, являются точками глобального минимума; стационарные точки, в которых Н (х) < 0, являются точками глобального максимума.
Исходя из вида исследуемой функции, проанализировать стационарные точки, в которых матрица вторых производных не является строго знакоопределенной.
Найденные точки локального экстремума исследуются на глобальный экстремум (если это возможно). В частности, если матрица Гессе неотрицательно (не положительно) определена на всем пространстве Е n , то все стационарные точки функции являются точками глобального минимума (максимума).
Численное решение задачи минимизации (1), как правило, связано с построением минимизирующей последовательности точек x0 , x1 , x2 ,…, xn ,…, обладающих свойством
f ( xk ) < f ( xk-1 ), k =0,1,… (3)
Общее правило построения минимизирующей последовательности имеет вид
x k+1 = x k + t k d k , k =0,1,…,
где х0 - начальная точка поиска; dk - приемлемое направление перехода из точки xk в точку xk+1 , которое обеспечивает выполнение условий (3) и называется направлением спуска; tk - величина шага. Начальная точка поиска задается исходя из физического содержания решаемой задачи и априорных данных о существовании и положении точек экстремума.
При решении вопроса о выборе численного метода рекомендуется оценить поведение линий уровня целевой функции в окрестностях предполагаемой точки экстремума. Число m = L/l , где L и l - максимальное и минимальное собственные значения гессиана функции f в предполагаемой точке экстремума x0 ( характеризующее разброс собственных значений оператора f (x)) , называется числом обусловленности гессиана функции f в точке x0 . Если m >> 1, то функция f называется плохо обусловленн ой или овражн ой . Овражность , то есть вытянутость линий уровня вдоль одного направления, приводит к тому, что градиентные методы поиска экстремума функции сходятся медленно.
В зависимости от наивысшего порядка частных производных функции f ( x), используемых для формирования dk и tk , численные методы принято делить на три группы:
Методы нулевого порядка, использующие информацию только о значениях функции f ( x) ( методы деформируемого многогранника, конфигураций). Эти методы могут применяться в тех случаях, когда функция задана неявно или не задана аналитически, но известен ряд значений функции или эти значения вычисляются непосредственно в ходе реализации алгоритма. Они также могут быть полезны в случаях, когда производные функции могут быть заданы аналитически, но их выражения очень громоздки.
Методы первого порядка, использующие информацию о значениях самой функции f ( x) и ее первых производных (методы наискорейшего градиентного спуска, дробления шага, Гаусса-Зейделя, Флетчера-Ривса).
Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) ( метод Ньютона и его модификации).
Метод конфигураций (Хука - Дживса)
Следует выделить два этапа метода конфигураций:
1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам.
Исследующий поиск начинается в точке х0 , называемой старым базисом. Направления поиска - координатные направления. По каждому направлению поочередно с шагом +t0 (-t0 ) проверяется выполнение условия (2) и в качестве нового базиса берется точка с координатами, полученными в результате удачных шагов из начальной точки по каждому направлению.
mirznanii.com
3. Условная оптимизация метод штрафных функций
5. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой ищется оптимум. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру поиска оптимума. Однако, напротив, процесс оптимизации становится более сложным, поскольку при наличии ограничений даже нельзя использовать применяемые нами выше условия оптимальности. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом.
Например, безусловный минимум функции f x x 22 имеет место в стационарной точкеx 2. Но если задача минимизации решается с учетом ограниче-
ния x 4 , | то будет найден условный минимум, которому соответствует точка | |
x 4. | Эта | точка не является стационарной точкой функции f(х), так как |
f 4 | 4 . Поэтому нужно изучить необходимые и достаточные условия опти- | |
мума в задачах с ограничениями, которые иначе называют задачами условной оптимизации.
5.2. Методы штрафных функций
Рассмотрим задачу условной оптимизации
f (x) min,x Rn , | (5.7) | ||
g j x0, | j 1,2,...,J , | (5.8) | |
hk x0, | k 1,2,...,K , | (5.9) | |
x l x x u ,i 1,2,...,n . | (5.10) | ||
i | i | i |
|
Такая задача также называется задачей нелинейного программирования. Говорят, что точкаx соответствует допустимому решению задачи нели-
нейного программирования, если для нее выполняются все ограничения, то есть соотношения (5.8–5.10).
Предполагается, что для вектора x* , являющегося решением задачи нели-
нейного программирования, известно некоторое начальное приближение x0 , возможно недопустимое. В методах штрафных функций строится последова-
тельность точек xm ,m 0,1,...,M , которая начинается с заданной точкиx0 и заканчивается точкойxM , дающей наилучшее приближение кx* среди всех точек
построенной последовательности. В качестве xm берутся точки решения вспомогательной задачи безусловной минимизации, полученной преобразованием исходной целевой функции с помощью так называемыхштрафных функций. В этих методах исходная задача условной оптимизации преобразуется в последовательность задач безусловной оптимизации.
Методы штрафных функций классифицируются в соответствии со способами учета ограничений-неравенств.В зависимости от того, являются ли эле-
менты последовательности xm допустимыми или недопустимыми точками, говорят ометодах внутренней и внешней точки соответственно. Если последова-
тельность xm содержит точки обоих типов, метод называютсмешанным.
Пусть необходимо решить задачу (5.7–5.10).Основная идея метода штрафных функций заключается в следующем. Строят вспомогательную функцию
J | K |
|
Q x,r,l f x rjGj gj x lk Hk hk x, | (5.11) | |
j 1 | k 1 |
|
такую, что приближенное решение задачи (5.7–5.10)получается в результате решенияпоследовательности задач безусловной минимизации функции
Q x,r,l min,x Rn . (5.12)
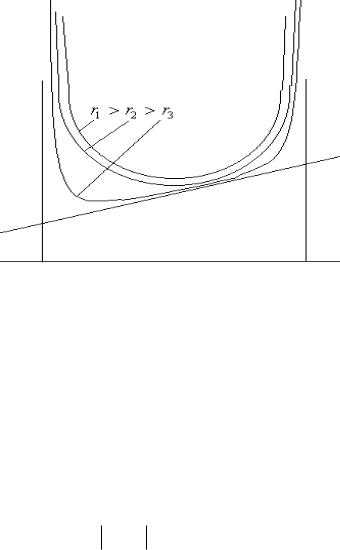
В методе внешних штрафных функций функцииH,G выбираются таким образом, чтобы они становились отличными от нуля (положительными) при нарушении соответствующего ограничения (рис. 22). А так как мы минимизиру-
ем (5.11), то движение в сторону нарушения становится невыгодным. Внутри допустимой области в данном методе функции H иG должны быть равны нулю.
Например, для ограничений-неравенствGj g j x 0 приg j x 0 .
Рис. 22. Поведение штрафных функций rjGj gj x в методах внешней точки, j=1,2,3 (снизу – функции rjGj (x) )
Приближенное решение задачи (5.7–5.10)получается в результате решения последовательности задач (5.12) приrj ,lk ,j 1,...,J ,k 1,...,K .
В методе барьерных функций функцииH,G выбираются отличными от нуля в допустимой области и такими, чтобы при приближении к границе допустимой области (изнутри) они возрастали, препятствуя выходу при поиске за границу области (рис. 23). В этом случае эти функции должны быть малыми (положительными или отрицательными) внутри допустимой области и большимиположительными вблизи границы (внутри области). Например, для ограничений
неравенств Gj g j x приg j x 0 .
Рис. 23. Поведение штрафных функций Gj gj x в методах барьерных функций, j=1,2,3
Такие методы называют еще методами внутренней точки. В алгоритмах, использующих функции штрафа данного типа, требуют, чтобы в процессе поиска точкаx всегда оставалась внутренней точкой допустимой области. Приближенное решение задачи(5.7–5.10)получается в результате решения последовательности задач (5.12) приrj ,lk 0,j 1,...,J ,k 1,...,K .
Для ограничений-равенствпри выборе функций штрафов обычно требуют, чтобыHk hk x 0 приhk x 0 .
Это могут быть, например, функции вида:
Hk hk x hk x, или
Hk hk x hk x , где – четное (например, =2).
Для ограничений-неравенствфункции штрафа подбирают таким образом, чтобы
Gj gj x0 | , при g j x 0, |
|
|
| |||||||||
Gj gj x0 | , при g j x 0 . |
|
|
| |||||||||
Этому требованию отвечают функции вида: |
| ||||||||||||
Gj gj x | 1 | g j x |
| g j x |
| , |
|
| (5.13) | ||||
|
|
|
| ||||||||||
|
|
|
| ||||||||||
| 2 |
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||||
| 1 |
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| ||||
Gj gj x |
|
|
| g j x | g j x |
| , | (5.14) | |||||
|
| ||||||||||||
| 2 |
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||||
при четном . При =2 штраф называют квадратичным.
В качестве барьерных функций для ограничений-неравенствмогут служить функции вида:
Gj gj x | 1 | , | (5.15) | |
| ||||
g j x | ||||
|
|
| ||
Gj gj xln gj x. | (5.16) | |||
Логарифмический штраф (5.16) – это барьерная функция, не определенная в недопустимых точках (то есть для таких x , чтоg(x) 0 ). Поэтому в тех случа-
ях, когда приходится иметь дело с недопустимыми точками (например, когда за-
данное начальное приближение x0 не является допустимым), требуется специальная процедура, обеспечивающая попадание в допустимую область.
Штраф, заданный функцией (5.15), не имеет отрицательных значений в допустимой области. Этот штраф, как и предыдущий, является барьером; в этом случае также возникают трудности, связанные с возможным появлением недо-
пустимых точек. |
|
|
|
|
|
|
|
|
| |
Часто функцию Q x,r,l | выбирают в виде |
| ||||||||
J |
|
| 1 |
| 1 | K |
|
|
| |
Q x, r,l f x R |
|
|
| hk x2 | , или | |||||
g |
| x | R | |||||||
j 1 | j |
| k 1 |
|
|
| ||||
|
|
|
|
|
|
| ||||
J |
|
|
|
|
|
| 1 | K |
| |
Q x, r,l f x Rln gj x | hk | x 2 , | ||||||||
| ||||||||||
j 1 |
|
|
|
|
|
| R k 1 |
| ||
где положительный штрафной параметр R 0 , монотонно убывая от итерации к итерации.
Последовательность действий при реализации методов штрафных функций или барьерных функций выглядит следующим образом:
1. На основании задачи (5.7–5.10)строим функцию (5.11). Выбираем начальной приближениеx и начальные значения коэффициентов штрафаrj ,lk ,
число итераций, точность безусловной оптимизации, точность соблюдения ограничений и т.д.
2.Решаем задачу (5.12).
3.Если полученное решение не удовлетворяет системе ограничений в случае использования метода штрафных функций, то увеличиваем значения коэффициентов штрафа и снова решаем задачу (5.12). В случае метода барьерных функций значения коэффициентов уменьшаются, чтобы можно было получить решение на границе.
4.Процесс прекращается, если найденное решение удовлетворяет системе ограничений с определенной точностью.
studfiles.net
Оптимизация функций отклика - Справочник химика 21
Математической моделью служит функция отклика, связывающая параметр оптимизации, характеризующий результаты эксперимента, с переменными параметрами, которыми варьируют при проведении опытов [c.6]Канонический анализ математической модели. Для целей оптимизации исследуемого объекта математическую. модель его часто представляют в типовой канонической форме. Каноническая форма уравнения регрессии второго порядка позволяет получить наглядную геометрическую интерпретацию функции отклика в области оптимума, что способствует как успешному продолжению исследований, так и удобному представлению результатов. [c.235]
ОПТИМИЗАЦИЯ ФУНКЦИИ ОТКЛИКА. [c.114]В ходе собственно эксперимента проводится измерение некоторых величин, которые характеризуют сущность изучаемого процесса или явления. Такие величины называются параметрами оптимизации, функциями отклика или просто откликами. Эксперимент предъявляет к отклику следующие требования отклик должен однозначно характеризовать изучаемый объект или процесс, быть количественно измеримым и статистически эффективным [53]. [c.106]
Оптимизация методом крутого восхождения по поверхности отклика. Задача оптимизации ставится таким образом необходимо определить экспериментально координаты экстремальной точки Х2° ".....функции y = f(xi, Х2,. .., Xk). Построим контурные сечения г/= onst поверхности отклика для /г = 2 (рис. 29, а). При традиционном эксперименте обычно фиксируют один из фак- [c.174]
Интерпретация и оптимизация функции отклика сильно упрощается, если модель является линейной. При полном отсутствии взаимодействия (корреляций) между факторами такая модель может стать адекватной. Для трехфакторного эксперимента нелинейная модель (6.6) в этом случае перейдет в линейную вида [c.111]
Параметр оптимизации (функция отклика) [c.186]
Функция отклика (параметр оптимизации) [c.116]
Оптимизируемую величину называют функцией отклика. Математически задача оптимизации — отыскание экстремума функции отклика. Будем называть задаваемые величины — факторами, их значения — уровнями фактора. [c.116]
Адекватная математическая модель, которой мы теперь располагаем, имеет вид полинома первой степени. Коэффициенты полинома являются частными производны.ми функции отклика по соответствующим переменным. Их геометрический с.мысл - тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению параметра оптимизации при изменении данного фактора. [c.290]
Далее был рассчитан градиент и реализованы опыты по крутому восхождению (табл. 2). Результаты оптимизации показали, что значение фактора Х3 стало граничным (функция отклика принимает максимальное значение) функция уо на каждом шаге оптимизации принимает значение, большее предыдущего, и не зависит от фактора Хз функция г/а принимает наибольшее значение в центре плана, т. е. при нуле-ных значениях факторов х Х2 и Хз. Очевидно, что для функций отклика Ук и Уо оптимальное соотношение компонентов имеет вид [c.89]
Это выражение, написанное в явном виде, является уравнением некоторой поверхности отклика в пространстве (й + 1)-мерного измерения. Таким образом, если все параметры правой части (6.1) определены, мы имеем полную информацию о виде и свойствах поверхности отклика, что является предпосылкой для начала оптимизации функции у. [c.109]
В качестве основной характеристики процесса (функции отклика) было выбрано произведение СД, где Л — изменение содержания бензола в смеси при прохождении через мембрану (Д — X бензола — У бензола). Следует отметить, что при оптимизации процессов мембранного разделения можно использовать и другие функции отклика, учитывающие одновременно скорость и селективность процесса. Наиболее правильно составленная функция отклика должна в своем экстремальном значении соответствовать минимальной стоимости процесса разделения. [c.196]
Опыт -У. X, X, функция отклика (параметр оптимизации) [c.58]
Использование принципов регрессионного и корреляционного анализа при обработке опытных данных позволяет найти зависимость между переменными и условия оптимума. В обоих случаях математической моделью является функция отклика, связывающая параметр оптимизации, характеризующий результаты эксперимента, с переменными, которые экспериментатор варьирует при проведении опытов [c.65]
С точки зрения химико-технологического исследования, величины х являются различными параметрами процесса (концентрации, давления, температуры, объемные скорости) они представляют собой независимые переменные и называются факторами. Функция у называется функцией отклика (или параметром оптимизации) и зависит от цели исследования — обычно это бывает селективность, степень конверсии, себестоимость, прибыль и т. д. [c.428]
При движении по градиенту проводят последовательно эксперименты, отличающиеся друг от друга по своим координатам на величину выбранного шага или на несколько шагов сразу. В результате экспериментально наблюдаемое значение функции отклика закономерно возрастает или убывает и, наконец, проходит через максимум или минимум. Найденная экспериментально достаточно малая окрестность экстремума называется почти стационарной областью, так как все первые производные здесь близки к нулю. Исследование почти стационарной области изложенным методом, очевидно, невозможно, потому что ее уже нельзя аппроксимировать плоскостью. Геометрическая интерпретация рассматриваемого метода оптимизации представлена на рис., ПО. [c.444]
Параметр, характеризующий результаты экспериментов, будем называть параметром оптимизации или функцией отклика. [c.32]
При оптимизации необходимо принимать во внимание ограничения. наложенные на влияющие факторы и некоторые функции отклика. [c.103]
Важно отметить, что как влияющие факторы, так и функции отклика могут изменяться только в определенных пределах. Так, концентрации реагентов не могут быть отрицательными, температура и давление в аппарате не могут превыщать безопасных пределов, себестоимость продукции должна быть не выще плановой и т. п. Следовательно, оптимизацию процессов, как правило, осуществляют в условиях ограничений на влияющие факторы и функции отклика. [c.21]
Величина, характеризующая уровень оптимизации процесса, называется критерием оптимальности. В частном случае критерием оптимальности может быть одна из функций отклика, характеризующих процесс. [c.21]
Оптимизация процесса представляет собой целенаправленный поиск значений влияющих факторов, при которых достигается экстремум критерия оптимальности (с учетом ограничений, наложенных на все влияющие факторы и функции отклика). [c.21]
Для оптимизации биотехнологических процессов микробиологического синтеза практически всегда необходимо знать концентрацию целевого продукта в конце ферментации. Поэтому для анализа связи между входными и выходными факторами первостепенное значение имеет модель функции отклика, связывающая входные факторы с концентрацией целевого продукта в конце культивирования. Истинный характер этой связи определяется множеством закономерностей процесса и не может быть одним и тем же для различных конкретных процессов, входных и выходных параметров. Тем не менее можно выделить наиболее существенную характерную особенность взаимодействия факторов в задаче оптимизации в случае поиска оптимальных рецептур питательных сред. Это взаимодействие типа лимитирования, известное в биологии как принцип Либиха. Словесное описание (описательная модель на естественном языке) данного принципа гласит [c.19]
Математической моделью служит функция отклика, связывающая параметр оптимизации, характеризующий результаты эксперимента, с переменными параметра- [c.6]
Задача построения интерполяционной модели системы, когда оптимизация функции отклика не производится, сводится к определению такой полиноми-нальной функции (уравнения регрессии), которая позволяет предсказать выходной параметр с определенной точностью во всех точках заранее заданной области (условие адекватности). Адекватность мате-матической модели устанавливается методами математической статистики. [c.43]
Известно, что математичес ие функции, в том числе и зависимость параметра оптимизации от выбранных параметров ("функция отклика ), могут быть представлены полиномом п-степени. Если отбросить члены второго порядка и выше, то функция отклика представляется плоскостью [c.13]
Иногда экоперИ Мент связан с отысканием оптимального значения функции отклика и тогда он называется экстремальным, а сама функция — параметром оптимизации. Однако чаще необходимо лишь установить временную зависимость прочности, а для ненагруженных конструкций — за,кон старения. Здесь экспериментатор сталкивается с необходимостью построения интерполяционной модели, соответствующей реальному процессу [c.102]
Морган и Деминг [102] также использовали экспериментальный подход к оптимизации процесса при одновременном изменении скорости газа-носителя и температуры колонки. Как конечную цель оптимизации они предложили хроматографическую функцию отклика ( hromatographi respon e iun tion) RF на основе введенного в (36) параметра разделения 0 [c.131]
Задача оптимизации в данном случае заключается в поиске условий или значений факторов, при которых оптическая плотность раствора заданной концентрации по олову будет максимальной. Вполне понятно, что при изменении независиипропорционально коэффициентам регрессии функция отклика будет эффективно отражать суммарное действие всех факторов. Для получения максимального значения функции отклика необходимо увеличивать те переменные, которые входят в уравнение регрессии с положительным знаком, и уменьшать те, которые входят с отрицательным. Бокс и Уилсон разработали прием достижения максимума в функции отклика, получивший название крутого восхождения. Техника расчета по этой методике заключается в следующем. Один из факторов, например Хг, выбирают как базовый и вычисляют для него произведения коэффициента регрессии Ьг на интервал варьирования ЛХг, т. е. гАХг, и определяют шаг движения по градиенту ЛХ. Выбор АХ является очень важным элементом расчета. Чрезмерно малый шаг потребует очень большого числа опытов, а при слишком большом шаге могут быть не замечены важные особенности системы или будет очень быстро превышен предел физически возможных значений фактора (например, концентрация раствора превысит растворимость соединения и т.д.). Величина шага должна, конечно, существенно превышать погрешность измерения фактора. Обычно принимают АХ АХ. Затем вычисляют отношение [c.376]
При рассмотрении полученных коэффициентов регрессий было установлено, что по всем параметрам оптимизации (кроме умо) линейные коэффициенты при первом переменном факторе отрицательны по знаку и в большинстве значимы. Так как целью исследования является получение максимальной величины для функции отклика (при этом все коэффициенты должны иметь положительный знак), то отрицательный знак при bi свидетельствует о том, что максимум функции отклика был проскочен , например, из-за большого интервала варьирования. Для большинства определяемых элементов, кроме Мп, V, Мо и 51, коэффициенты взаимодействия типа ХгХ] и Х1Х2Х3 незначимы и не оказывают существенного влияния на параметр оптимизации и на ошибку воспроизводимости при данном интервале варьирования. [c.167]
Анализ расчетных данных показывает, что гипотеза об адекватном представлении модели процесса данной системой уравнений может быть принята, так как значения коэффициентов нргг большей части нелинейных членов уравнений соизмеримы с ошибкой их определения, к сам вклад этих членов в величины функций оптимизации невысок. Кроме того, расчетное значение критерия Фишера (/ р ,сч ) Для всех функций отклика меньше табличного (fтлaл) [c.33]
Использовать эти функции отклика при планировании эксперимента неудобно, и лучше находить при опытах регрессионные уравнения для тех функций, которые непосредственно влияют на экономические показатели, прежде всего для степени конверсии, селективности и производительности. После этого из анализа различных затрат выводят уравнение себестоимости или прибыли, связывающее их как с первоначальными функциями отклика, так и с независимыми переменными (давлениями, температурой, количеством катализатора или инициатора, объемной скоростью или временем), вычисляют для каждого опыта плана экономический критерий оптимизации и находят обычным образом регрессионное уравнение, связывающее этот критерий с независимыми переменными. Далее можно использовать описанный способ крутого восхождения . [c.447]
Среди всех и.меющихся функций отклика, описывающих объект оптимизации, выбирают одну наиболее важную и принимают ее в качестве критерия оптимальности у. Затем указывают ограни- [c.99]
Усовершенствование модели проводилось в направлении уменьшения суммы квадратов отклонений. Оптимизация выбранных параметров проводилась путем преобразования функции отклика в кононическое уравнение второго порядка. [c.405]
Интерпретация знаков коэффициентов при оптимизации зависит от того, ищем ли мы максимум или минимум функции отклика. Если у (в нашем случае Уд), то увеличение значений всех факторов, коэффициенты которых имеют знак плюс, благоприятно, а знак минус - неблагоприятнф. Если же (у нас У1.У2,У4). тоу наоборот, благоприятно увеличение значений тех факторов, знаки коэффициентов которых отрицательны. При оценке влияния эффектов взаимодействия факторов на тараметры оптимизации пришто правило, что если эффект взаимодействия имеет положительный знак, то для увеличения параметра оптимизации требуется одновременное увеличение или уменьшение значений, факто-, ров, например х = +1 и х = +1 или х, = -1 и Х2 = -Г. Для уменьшения параметра оптимизации факторы должны одновременно изменяться в разных направлениях, например х = [c.45]
Функция желательности. Задачу оптимизации процессов, ха-ракгеризующихся несколькими откликами, обычно сводят к задаче оптимизации по одному критерию с ограничениями в виде равенств или неравенств. В зависимости от вида поверхности отклика и ха-ракгера ограничений для оптимизации предлагается использовать методы неопределенных множителей Лагранжа, линейного и нелинейного программирования, ридж-анализ [10] и др. К недостаткам этих способов решения задачи оптимизации следует отнести вычислительные трудности. В частности, при описании поверхности отклика полиномами второго порядка решение задачи на условный экстремум с применением неопределенных множителей Лагранжа приводит к необходимости решать систему нелинейных уравнений. Поэтому одним из наиболее удачных способов решения задачи оптимизации процессов с большим количеством откликов является использование предложенной Харрингтоном [23] в качестве обобщенного критерия оптимизации так называемой обобщенной функции желательности О. Для построения обобщенной функции желательности О предлагается преобразовать измеренные значения от- [c.207]
chem21.info
Оптимизация функций | Бесплатные курсовые, рефераты и дипломные работы
Постановка задачи: на множестве (допустимое множество) задана функция (целевая функция) одного или нескольких аргументов, требуется приближенно с заданной точностью найти те значения аргумента (аргументов) из X, в которых эта функция принимает минимальное значение:
На функцию , как правило, накладываются те или иные ограничения. Минимизировать функцию, пользуясь методами:
Метод половинного деления (дихотомия).Предполага-
Рис. 1. Дихотомия
ется, что и функция унимодальна на заданном отрезке. … Вначале выбираются две пробные точки
где (см. рис. 1). Затем исходный отрезок, содержащий точку минимума, сокращается до следующим способом: если , то выбирается левая часть отрезка, полагаем , , а если , то — правая, , . К полученному отрезку применяется та же процедура выбора пробных точек и сокращения отрезка локализации минимума и т.д., пока не станет
(1)
В качестве приближенного решения можно взять точку
Метод золотого сечения.Как и в предыдущем методе, предполагается, что и функция унимодальна на этом отрезке. Вначале выбираются две пробные точки
Исходный отрезок сокращается до следующим способом: если , то выбирается левая часть отрезка, полагаем , , , а если , то — правая, , , . В алгоритме метода золотого сечения, в отличие от дихотомии, на всех последующих итерациях производится расчет только той точки и значение функции в ней, которые необходимо обновить. При выполнении неравенства вычисляются и , а при — и . Процедура прекращается, когда становится истинным неравенство (1).
Метод градиентного спуска.Алгоритм использует тот факт, что направление, обратное градиенту функции есть направление её самого быстрого убывания (см. Рис. 2). Здесь допустимое множество и функция предполагается непрерывно дифференцируемой в указанной области.
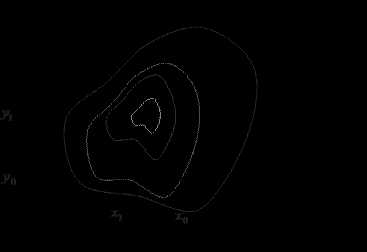
Рис.2. Метод градиентного спуска
Задав произвольно начальную точку и начальный шаг вычислить и
Если на -ой итерации , то шаг уменьшить вдвое и повторить вычисления. Уменьшать шаг в два раза до тех пор, пока не будет выполнено неравенство
К следующей итерации перейти с шагом, определённым на предыдущей итерации. Процедура останавливается, когда выполняется соотношение
refac.ru