4.5.6. Непрямые методы условной оптимизации. Методы условной оптимизации
8 9 Методы условной оптимизации
8.9. Методы условной оптимизации
В общем случае задача может содержать ограничения в виде равенств и неравенств, которые и определяют допустимое множество D. Наличие ограничений существенно усложняет решение задачи оптимизации. В большинстве случаев условный оптимум достигается на границе допустимого множества, при этом даже унимодальная функция может иметь на границе несколько локальных экстремумов.
Из большого числа методов условной оптимизации можно выделить 3 основные группы:
методы возможных направлений: метод проектирования градиента, методы Зойтендейка, Вулфа и др.;
методы штрафных и барьерных функций;
модификации методов безусловной оптимизации.
Методы первой группы отличаются способом определения возможных направлений. Направление d в точке xkD называется возможным направлением, если существует 0, при котором
Эти условия означают, что на направлении d найдутся допустимые точки, в которых значение функции лучше, чем в точке xk.
Ниже рассматривается один из методов возможных направлений.
8.9.1. Метод проектирования градиента
Градиент дает направление, в котором функция возрастает с наибольшей скоростью. Однако при условной оптимизации оно, как правило, не является возможным направлением. Поэтому используют не сам градиент (антиградиент), а его проекцию на поверхность ограничений, точнее, на плоскость, аппроксимирующую эту поверхность в текущей точке. Очевидно, что проекция градиента определяет направление наискорейшего изменения функции на поверхности ограничений.
Приведем один из вариантов метода проектирования градиента сначала для задачи с ограничениями-равенствами, а затем для общего случая. Метод применим, если целевая функция и все функции ограничений дифференцируемы.
Пусть ограничения заданы в виде
(8.55)
Найдем возможное направление l, на котором скорость изменения целевой функции максимальна:
(8.56)
В допустимой области D функции j постоянны. Поэтому искомое направление должно удовлетворять системе равенств
(8.57)
Из связи направления с координатами следует:
что перепишем в виде
(8.58)
Таким образом, для нахождения наилучшего возможного направления необходимо решить задачу оптимизации (8.56) – (8.58). Так как условия имеют вид равенств, а функции дифференцируемы, для решения этой вспомогательной задачи воспользуемся методом Лагранжа.
Запишем функцию Лагранжа:
. (8.59)
Неизвестными в ней являются векторы и . Взяв производные и приравняв их нулю, получаем
Отсюда выразим компоненты искомого вектора:
(8.60)
Подставив (8.60) в (8.58), находим:
С учетом этого выражения формула (8.60) принимает вид
(8.61)
После раскрытия скобок окончательно имеем:
(8.62)
Так как направление ищется в конкретной точке, то все производные в (8.62) – известные константы. Поэтому система уравнений (8.62) является линейной системой относительно j. Ее решение не вызывает затруднений (при условии, что матрица системы не является особенной). Найдя значения j и подставив их в (8.61), получаем компоненты проекции градиента (в знаменателе (8.61) имеем длину проекции градиента). Движение осуществляется в направлении, противоположном проекции.
Аналогично градиентному методу новая точка вычисляется по формуле
. (8.63)
Алгоритм.
Задать начальную точку, удовлетворяющую системе (8.55), начальное значение h0и точность по величине проекции градиента .
В текущей точке вычислить градиенты всех функций (f и j) и решить систему (8.62).
Вычислить проекцию градиента по формуле (8.61).
Проверить: если завершить поиск.
Вычислить новую точку по формуле (8.63).
Проверить: если значение целевой функции улучшилось, перейти на шаг 2, иначе уменьшить hk в два раза и перейти на шаг 5.▲
Качественный характер работы алгоритма иллюстрирует рис. 8.39. Здесь функции зависят от 2-х переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество.
При линейных ограничениях могут возникать проблемы поиска лишь при очень малых значениях градиентов функций ограничений и совпадении их направлений, так как это приводит к вырожденности матрицы системы (8.62).
В случае нелинейных ограничений движение на основе линейной аппроксимации нарушает равенства. Поэтому в алгоритм необходимо внести изменения, обеспечивающие выполнение равенств с необходимой точностью . С этой целью алгоритм дополняется проверкой величины невязки, которая выполняется в каждой новой точке. Если , то включается процедура коррекции, заключающаяся в минимизации невязки:
(8.64)
Для решения задачи (8.64) можно применить любой метод безусловной оптимизации, но в данном контексте целесообразен метод градиентов. При этом значения (n-m) переменных фиксируются, так как для выполнения равенств достаточно m переменных. Понятно, что при частых коррекциях трудоемкость алгоритма значительно возрастает.
Теперь рассмотрим случай, когда ограничения заданы в виде неравенств j(x)0. Поиск начинается из точки, в которой удовлетворяются все ограничения. Пока они выполняются как строгие, движение осуществляется по градиентному методу. Когда достигается граница допустимого множества, одно или несколько ограничений обращаются в равенства. Такие ограничения называют активными. В точках с активными ограничениями направление движения определяется по проекции градиента на поверхность этих ограничений, то есть применяется вышеприведенный алгоритм. Пример поиска минимума при двух линейных неравенствах показан на рис. 8.40. Очевидно, что при смешанных и нелинейных ограничениях алгоритм весьма существенно усложняется и требует большого объема вычислений. Поэтому метод проектирования градиентов целесообразно применять при линейных ограничениях.
8.9.2. Метод штрафных функций
Совершенно иной подход используется в методах штрафных и барьерных функций. Ограничения задачи специальным образом отражаются в критерии, в результате чего критерий модифицируется, а исходная задача на условный экстремум сводится к задаче на безусловный экстремум.
В методе штрафных функций в критерий вводится штраф при нарушении условий задачи. Пусть в общем случае имеем задачу
f(x) min; (8.65)
i(x) 0, ; (8.66)
i(x) = 0 , . (8.67)
Тогда можно построить вспомогательную функцию
(x) = f(x) + H(x), (8.68)
где H(x)–функция штрафа, - параметр штрафа.
Вспомогательная функция играет роль модифицированного критерия, который при выполнении всех ограничений должен совпадать с исходным. Поэтому необходимо, чтобы в допустимой области Н(х) равнялась нулю, а вне ее была положительной. Для задачи (8.65)-(8.67) функция штрафа включает две составляющие Н(х) =Н(x) + Н(x), учитывающие ограничения-неравенства и ограничения-равенства соответственно и удовлетворяющие условиям
(8.69)
Возможны разные конструкции функций, обладающих указанными свойствами. Типичные представители составляющих штрафной функции имеют вид
где р – натуральное число. Для дифференцируемости функций берут четные значения р, обычно р = 2.
Чем больше , тем сильнее влияет функция штрафа и, значит, тем точнее выполняются условия задачи.
Пример 8.8. Дана задача
f(x) = x min;
(x)=3 – x 0.
Ответ очевиден: x*=3. Теперь сведем эту задачу к определению безусловного экстремума вспомогательной функции. Построим штрафную функцию в соответствии с (8.69): H = [max (0, 3-x)]2. Тогда приходим к задаче
=x+[max (0, 3-x)]2 min.
На рис. 8.41 и 8.42 показаны функции H и для двух значений . Видно, что точки минимума вспомогательной функции с увеличением приближаются к точке условного минимума исходной задачи. Такой же вывод следует из аналитического решения. Действительно, при x<3 вспомогательная функция имеет вид
= x + (3 - x)2.
Находим минимум этой функции:
Отсюда получаем
Пример 8.9. Рассмотрим влияние параметра шага в задаче
Здесь и На рис. 8.43 построены линии уровня функции для разных значений и линия ограничения . При =0 имеем =f, и минимум достигается в точке безусловного минимума f: x1=x2=1. С увеличением меняется форма линий уровня и положение минимума. При =1 минимум смещается к линии ограничения, а при =1000 он практически точно совпадает с условным минимумом задачи.
В обоих примерах с увеличением генерируемые точки приближаются к оптимальному решению извне допустимого множества. Поэтому ряд авторов называют рассматриваемый метод методом внешних штрафов.
Таким образом, чтобы безусловный минимум вспомогательной функции был близок к условному минимуму решаемой задачи, необходимо брать очень большое значение , теоретически бесконечное. Однако при больших возникают серьезные трудности при поиске минимума вспомогательной функции. Поэтому предлагается решать последовательность задач минимизации с возрастающими значениями . При этом в качестве начальной точки следующей задачи берется оптимальная точка предыдущей. Такой прием использован в следующем алгоритме штрафных функций.
Алгоритм.
1. Задать: начальную точку x0, точность , начальное значение 0 и число > 1.
2. Минимизировать (x) одним из методов безусловной оптимизации, в результате чего определяется .
3. Проверить: если , то остановиться, приняв за оптимальное решение задачи.
Положить , за начальную точку принять и вернуться на шаг 2.▲
Рекомендуется выбирать значения параметров алгоритма из диапазонов: 0(0,1], (1,10]. Начальную точку следует задавать в недопустимой области.
Пример 8.10. Алгоритмом штрафных функций решить задачу
Возьмем начальную точку x0=(-5;5), 0=0,21, =5 и =0,0001. Применяя для минимизации метод Ньютона, получаем результаты, представленные в табл. 8.4.
Таблица 8.4
№ итерации | | x1 | x2 | f | | H |
0 | 0.21 | -5 | 5 | 270 | 283.533 | 13.533 |
1 | 1.05 | -0.191 | -0.132 | -0.094 | 0.939 | 1.032 |
2 | 5.25 | -0.209 | -0.169 | -0.09 | 5.035 | 5.125 |
3 | 26.25 | -0.654553 | -1.059105 | 1.651353 | 13.504372 | 11.853019 |
4 | 131.25 | -0.990765 | -1.731532 | 5.068137 | 7.691651 | 2.623514 |
5 | 656.25 | -1.046856 | -1.843717 | 5.814225 | 6.343889 | 0.529664 |
6 | 3281.25 | -1.057736 | -1.865478 | 5.964774 | 6.070887 | 0.106113 |
7 | 16406.25 | -1.059899 | -1.869804 | 5.994933 | 6.016163 | 0.02123 |
8 | 82031.25 | -1.060331 | -1.870668 | 6.000967 | 6.005213 | 0.004246 |
9 | 410156.25 | -1.060417 | -1.870841 | 6.002174 | 6.003023 | 0.000849 |
10 | 2050781.25 | -1.060434 | -1.870876 | 6.002415 | 6.002585 | 0.00017 |
11 | >107 | -1.060434 | -1.870884 | 6.002469 | 6.002503 | 3.397E-05 |
Как следует из таблицы, решение с заданной высокой точностью получено за 11 итераций алгоритма. Заметим, что несмотря на увеличение значение H сходится к нулю, обеспечивая сходимость алгоритма. Траектория поиска и линии уровня функции f изображены на рис. 8.44.▲
Другой пример поиска методом штрафных функций приведен на рис. 8.45 для задачи
Поиск проведен из начальной точки (-2;-7) с параметрами 0=0,1 и =2. Здесь, как и в предыдущем примере, на первой итерации алгоритма движение направлено в сторону безусловного минимума целевой функции. Это объясняется небольшим начальным значением параметра штрафа, при котором основное влияние на направление оказывает целевая функция. С возрастанием направление поиска ориентируется на условный экстремум.
Еще один пример поиска показан на рис. 8.46 для задачи
Здесь поиск производился при 0=1 и =10. Такие параметры обусловили другой характер движения к условному минимуму: первая итерация уже не приводит в окрестность безусловного экстремума и траектория не имеет резких изменений направления поиска.
Таким образом, выбор параметров поиска имеет существенное влияние на эффективность алгоритма.
textarchive.ru
4.9. Методы условной оптимизации
4.9.1. Общие положения
В общем случае задача может содержать ограничения в виде равенств и неравенств, которые и определяют допустимое множество D. Наличие ограничений существенно усложняет решение задачи оптимизации. В большинстве случаев условный оптимум достигается на границе допустимого множества, при этом даже унимодальная функция может иметь на границе несколько локальных экстремумов.
Из большого числа методов условной оптимизации можно выделить 3 основные группы:
методы возможных направлений: метод проектирования градиента, методы Зойтендейка, Вулфа и др.;
методы штрафных и барьерных функций;
модификации методов безусловной оптимизации.
Методы первой группы отличаются способом определения возможных направлений. Направление d в точке xkD называется возможным направлением, если существует 0, при котором
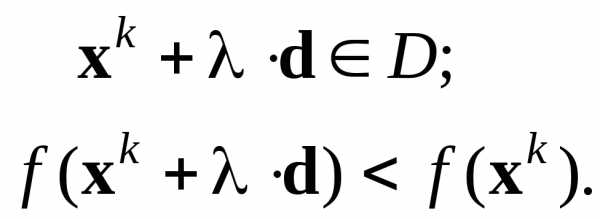
Эти условия означают, что на направлении d найдутся допустимые точки, в которых значение функции лучше, чем в точке xk.
Ниже рассматривается один из методов возможных направлений.
4.9.2. Метод проектирования градиента
Градиент дает направление, в котором функция возрастает с наибольшей скоростью. Однако при условной оптимизации оно, как правило, не является возможным направлением. Поэтому используют не сам градиент (антиградиент), а его проекцию на поверхность ограничений, точнее, на плоскость, аппроксимирующую эту поверхность в текущей точке. Очевидно, что проекция градиента определяет направление наискорейшего изменения функции на поверхности ограничений.
Приведем один из вариантов метода проектирования градиента сначала для задачи с ограничениями-равенствами, а затем для общего случая. Метод применим, если целевая функция и все функции ограничений дифференцируемы.
Пусть ограничения заданы в виде
(4.55)
Найдем возможное направление l, на котором скорость изменения целевой функции максимальна:
(4.56)
В допустимой области D функции j постоянны. Поэтому искомое направление должно удовлетворять системе равенств
(4.57)
Из связи направления с координатами следует
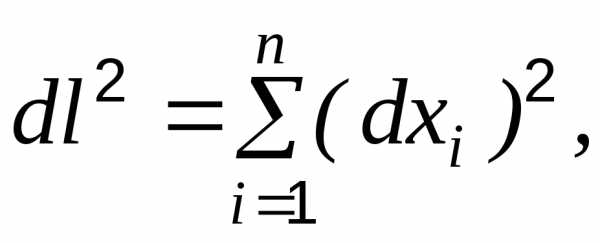
что перепишем в виде
 (4.58)
(4.58)
Таким образом, для нахождения наилучшего возможного направления необходимо решить задачу оптимизации (4.56)–(4.58). Поскольку условия имеют вид равенств, а функции дифференцируемы, для решения этой вспомогательной задачи воспользуемся методом Лагранжа.
Запишем функцию Лагранжа:
. (4.59)
Неизвестными в ней являются векторы 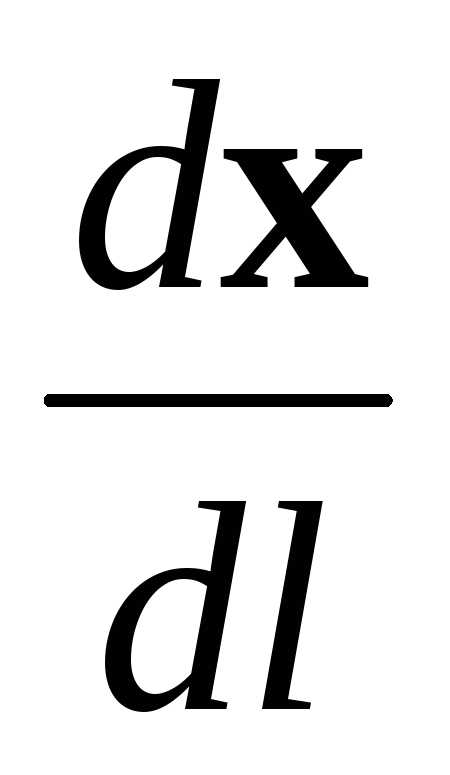 и. Взяв производные
и. Взяв производные 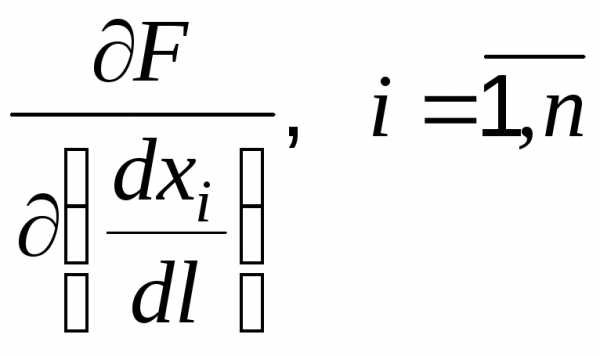 и приравняв их нулю, получаем
и приравняв их нулю, получаем
Отсюда выразим компоненты искомого вектора:
(4.60)
Подставив уравнение (4.60) в формулу (4.58), находим
С учетом этого выражения формула (4.60) принимает вид
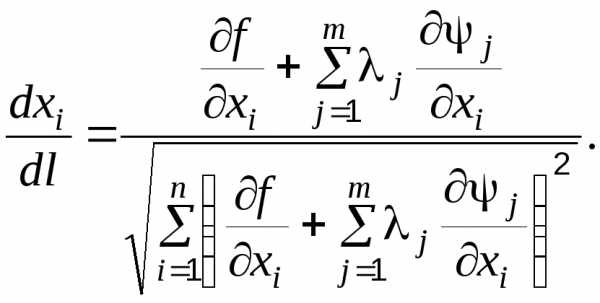 (4.61)
(4.61)
Для определения неизвестных множителей j воспользуемся системой (4.57). Подставив в нее формулу (4.61), получаем
После раскрытия скобок окончательно имеем
(4.62)
Так как направление ищется в конкретной точке, то все производные в уравнении (4.62) – известные константы. Поэтому система уравнений (4.62) является линейной системой относительно j. Ее решение не вызывает затруднений (при условии, что матрица системы не является особенной). Найдя значения j и подставив их в формулу (4.61), получаем компоненты проекции градиента (в знаменателе (4.61) имеем длину проекции градиента). Движение осуществляется в направлении, противоположном проекции.
Аналогично градиентному методу новая точка вычисляется по формуле
. (4.63)
Алгоритм
Задать начальную точку, удовлетворяющую системе (4.55), начальное значение h0 и точность по величине проекции градиента .
В текущей точке вычислить градиенты всех функций (f и j) и решить систему (4.62).
Вычислить проекцию градиента по формуле (4.61).
Проверить: если завершить поиск.
Вычислить новую точку по формуле (4.63).
Проверить: если значение целевой функции улучшилось, перейти на п. 2, иначе уменьшить hk в два раза и перейти на п. 5.
Качественный характер работы алгоритма иллюстрирует рис. 4.38. Здесь функции зависят от 2 переменных, поэтому в каждой точке на линии ограничения может быть всего 2 направления, лучшее из которых определяет проекция градиента. В многомерной задаче таких направлений бесконечное множество.
Рис. 4.38. Качественный характер работы алгоритма
При линейных ограничениях могут возникать проблемы поиска лишь при очень малых значениях градиентов функций ограничений и совпадении их направлений, так как это приводит к вырожденности матрицы системы (4.62).
В случае нелинейных ограничений движение на основе линейной аппроксимации нарушает равенства. Поэтому в алгоритм необходимо внести изменения, обеспечивающие выполнение равенств с необходимой точностью . С этой целью алгоритм дополняется проверкой величины невязки, которая выполняется в каждой новой точке. Если 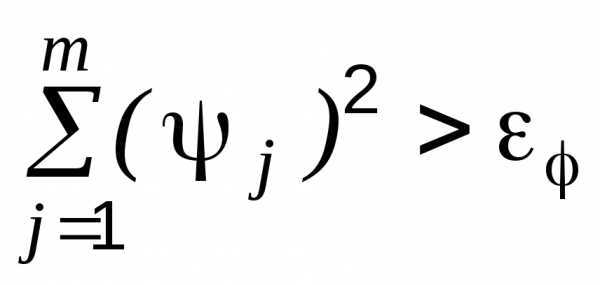 , то включается процедура коррекции, состоящая в минимизации невязки:
, то включается процедура коррекции, состоящая в минимизации невязки:
 (4.64)
(4.64)
Для решения задачи (4.64) можно применить любой метод безусловной оптимизации, но в данном контексте целесообразен метод градиентов. При этом значения (n – m) переменных фиксируются, так как для выполнения равенств достаточно m переменных. Понятно, что при частых коррекциях трудоемкость алгоритма значительно возрастает.
Теперь рассмотрим случай, когда ограничения заданы в виде неравенствj(x) 0. Поиск начинается из точки, в которой удовлетворяются все ограничения. Пока они выполняются как строгие, движение осуществляется по градиентному методу. Когда достигается граница допустимого множества, одно или несколько ограничений обращаются в равенства. Такие ограничения называют активными. В точках с активными ограничениями направление движения определяется по проекции градиента на поверхность этих ограничений, т.е. применяется вышеприведенный алгоритм. Пример поиска минимума при двух линейных неравенствах показан на рис. 4.39.
Очевидно, что при смешанных и нелинейных ограничениях алгоритм весьма существенно усложняется и требует большого объема вычислений. Поэтому метод проектирования градиентов целесообразно применять при линейных ограничениях.
studfiles.net
4.5.6. Непрямые методы условной оптимизации
F(X,а) необходимо начинать с внутренней точки областиG. При этом в процессе оптимизации траектория спуска никогда не выйдет за пределы допустимой области. Все перечисленные особенности функции Ф(X,а) определили наименование рассматриваемой группы методов.
Таким образом, внутренняя штрафная функция Ф(X,а) должна обладать следующими свойствами:
→ ∞ приx G,
Φ(X,a)= → 0 приx G,x dG,a → 0,→ ∞ приx G,x → dG,
где dG – граница областиG. |
|
Внутренние штрафные | функции задаются в форме |
Φ(X,a)= a∑m ϕj (zj (X)), где ϕj | – непрерывные дифференцируе- |
j=1 |
|
мые функции, определяемые ограничениями-неравенствамиисходной задачи нелинейного программирования. В качестве внут-
ренних штрафных | функций используют, например, такие: | ||
Φ(X,a)= a∑m | 1 |
| , Φ(X,a)= −a∑m ln(zj (X)). |
| |||
j=1 z j(X) | j=1 | ||
Алгоритм метода внутренних штрафных функций состоит в следующем:
1.В качестве начальной точки X[0] выбирают произвольную внутреннюю точку областиG.
2.Задаются некоторой монотонно убывающей сходящейся к нулю последовательностью {ak},k=1,2,..., положительных чисел.
3.Для первого элемента а1 этой последовательности решают задачу безусловной минимизации функцииF(X,а1 ) одним из рассмотренных выше методов, в результате чего определяют точку
X[1]=X(а1). Эту точку используют в качестве начальной для решения задачи поиска минимума функцииF(X,а2 ) и так далее.
4.Вычисления прекращают при выполнении условий |f(X[k])–
f(X[k–1])|≤ε,||X[k]–X[k–1]||≤δ, гдеε,δ – заданные числа, определяющие точность вычислений.
Таким образом, метод внутренних штрафных функций предусматривает последовательное решение задач безусловной минимизации функций F(X,аk ),k=1,2,..., причем решение предыдущей задачиX(аk) используется в качестве начальной точки для поиска
studfiles.net
6.8. Методы условной оптимизации
где H k – матрица, рассчитываемая по специальному алгоритму на основеH k 1 . Заметим, что (136) применимо и к методу наискорейшего спуска, еслиH k
– единичная матрица. Если принять H k Яk 1, гдеЯ k 1 – обратная матрица вторых частных производныхF(X ) поX , называемая матрицей Гессе, то мы имеем метод Ньютона, относящийся к методам второго порядка. Методы второго порядка в САПР практически не применяютсяиз-затрудностей расчета матрицы Гессе и плохой сходимости вдали от минимума. Поэтому вместоЯ k 1 используется ее приближение, рассчитываемое в методе переменной метрики без использования вторых производныхF(X ) поX .
Метод штрафных функций основан на преобразовании исходной задачи (116) с ограничениями к задаче без ограничений с применением к последней методов безусловной оптимизации. Преобразование проводится по формуле(X ) F(X ) (X ), где(X ) иF(X ) – соответственно новая и первоначальная целевые функции,(X ) – функция штрафа, учитывающая нарушенные ограничения. В методе штрафных функций, называемомметодом внешней точки, функция штрафа
N | m |
|
(X )r1 min 0,i ,(X )2 | r2 (j (X ))2 , | (137) |
i 1 | j 1 |
|
где N иm – количества ограничений соответственно типа неравенствi (X ) 0 и равенствj (X ) 0 в исходной задаче математического программирования (116),r1 иr2 – коэффициенты, подбираемые из компромиссного удовлетворения требований точности и экономичности вычислений.
Метод внутренней точки, или метод барьерных функций, характеризуется функцией штрафа

(x)
N |
| m |
|
(X )r1 1i X | r2 (j (X))2 . | (138) | |
i 1 |
| j 1 |
|
На рис. 49 показаны функции (x) | и F (x ) для одномерного случая при | ||
наличии ограничения (x) 0 . Точка условного минимума х* функцииF (x ) в методе штрафных функций становится точкой безусловного минимума функции
, чем и обеспечивает правильность получаемых результатов.
Метод проекции градиента, относящийся к методам первого порядка, обладает высокой эффективностью среди методов, непосредственно применимых к задачам с ограничениями типа равенств. Его сущность заключается в том, что шаги поиска осуществляются не в направлении антиградиента (134), как в методе наискорейшего спуска, а в направлении проекции антиградиента на гиперповерхность ограничений, задаваемую системой равенств (X ) 0 . К началу каждого шага условие(X ) 0 должно выполняться, что достигается предварительным спуском на гиперповерхность ограничений. Таким образом, метод проекций градиента состоит из чередующихся спусков на гиперповерхность ограничений и шагов вдоль гиперповерхности в направлении, противоположном проекции градиента целевой функции. При поиске максимина в систему уравнений, задающую
гиперповерхность ( X ) , включаются уравнения | вида s'(X )s' ' (X ) | 0 , где | |||
s' (X ) – запас работоспособности | некоторого выходного | параметра, | причем | ||
включение осуществляется | на | k -омшаге | поиска, | если окажется | |
s' (X k )s' ' (X k 1), где s' ' (X ) | – целевая функция. |
|
|
| |
(x )
F(x)
(x )
178
X
studfiles.net
Метод условной оптимизации
Этот метод, также как и метод суперкритерия, предполагает, что критерии не равнозначны. Мы можем выбрать самый значимый для нас критерий, но не можем оценить вес каждого критерия численно (не можем сказать, сколько рублей стоит 1 час). В этом случае в качестве единственного критерия мы оставляем самый значимый для нас критерий, а остальные критерии считаем ограничениями (условиями). Далее различают два случая введения ограничений: типа равенств и типа неравенств. Первый случай проще осуществляется технически, но менее адекватен реальности. Второй более адекватен реальности, но труднее осуществляется технически.
Пример. Как и в предыдущем примере будем выбирать лучший подарок по двум критериям: q1 - цена подарка, главный критерий; q2 - время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин.
Рассмотрим случай ограничений типа равенств. Зададим ограничение по времени (так как это не главный для нас критерий): время, затрачиваемое на приобретение подарка q2 = 1 час. 20 мин. Выберем теперь из всех подарков такие, у которых q2 = 1 час. 20 мин. Видим, что таких подарков в нашем списке нет. Таким образом, далее мы осуществляем выбор на пустом множестве альтернатив. Это значит, что мы отвергли все предложенные альтернативы.
Естественно, что в реальных ситуациях принятия решений ограничения типа равенств встречаются не часто. Более адекватный случай – ограничения типа неравенств. Зададим в нашем примере ограничения типа неравенств. Будем считать, что нам надо купить подарок не ровно за 1 час. 20 мин. (как это было в ограничении типа равенств), а не более, чем за 1 час 20 мин., т.е. 0 мин. q2 1 час 20 мин. Выбираем из всего множества подарков те, которые покупаются не более, чем за 1 час 20 мин. В это множество вошли второй и третий подарок. Теперь мы выбираем из них наилучший на основании только главного критерия – цены. Наилучшим будет второй подарок, т.к. у него меньшая цена (350 руб.)
Достоинства метода:
не вводится никаких новых критериев;
выявляется только самый значимый критерий, но численные значения весов не определяются.
Недостатки метода:
ограничения типа равенств часто являются неадекватными реальным ситуациям принятия решений;
с ограничениями типа неравенств часто технически сложно решать задачу принятия решений.
Метод уступок
На практике при решении многокритериальных задач выбора при неравнозначных критериях часто пользуются методом уступок. Как и в методе условной оптимизации, выбирают главный критерий. Далее задают значение вспомогательного критерия. После этого при фиксированном значении вспомогательного критерия ищут альтернативу с оптимальным значением главного критерия. Если значение главного критерия удовлетворяет лицо, принимающее решение, то найденная альтернатива принимается. Если значение главного критерия не удовлетворяет лицо, принимающее решение, то он пытается «уступить», т.е. снизить значение второстепенного критерия в надежде получить выигрыш в значении главного критерия. Если при сделанной уступке лицо, принимающее решение не выигрывает в значении главного критерия, то он либо продолжает процесс уступок, либо принимает какое-то решение из предыдущих, либо отвергает все альтернативы.
Поясним суть этого метода на рисунке. Пусть q1(x) - главный критерий. Зафиксируем значение второстепенного критерия q2(x) = C21. При данном фиксированном значении этого критерия (на рисунке это нижняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*1. Предположим, что значение главного критерия q1(x1*1) нас не удовлетворяет.
Мы делаем уступку в значении второстепенного критерия q2(x), полагая его значение q2(x) = C22 > C21. Далее при этом значении критерия q2(x) (на рисунке это средняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*2. Предположим, что значение главного критерия q1(x1*1) нас не удовлетворяет.
Мы готовы сделать еще уступку в значении второстепенного критерия q2(x), полагая его значение q2(x) = C23 > C22. Далее при этом значении критерия q2(x) (на рисунке это верхняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q1(x). Это точка x1*3. Значение главного критерия q1(x1*3) = Q нас теперь удовлетворяет. На этом процесс поиска решения прекращается. Найденная альтернатива x1*3 считается принятой.
Пример. Выбираем лучший подарок по двум критериям: q1 - цена подарка, главный критерий; q2 - время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего подарков соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение 2 часа, 1 час и 30 мин.
Зафиксируем значение второстепенного критерия q2(x) = 20 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это множество пусто. Такое положение нас не удовлетворяет. Сделаем уступку по времени. Положим q2(x) = 30 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок третий. Посмотрим значение главного критерия – цену. Допустим, что его цена 400 руб. нас не устраивает. Вновь делаем уступку по времени. Положим q2(x) = 1 час. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок второй. Посмотрим значение главного критерия – цену. Допустим, что его цена 350 руб. нас устраивает, т.е. мы считаем цену нашей уступки по времени (30 мин.) адекватной цене нашего выигрыша в главном критерии (50 руб.). Тогда процесс выбора окончен. Мы выбираем второй подарок.
Достоинства метода:
Недостатки метода:
метод не гарантирует, что за достаточно большое число шагов найдётся удовлетворяющее решение. Это возможно из-за того, что цена уступок не будет адекватной цене нашего выигрыша.
studfiles.net
4.5.5. Прямые методы условной оптимизации
1. В качестве первой вершины начального комплекса выбирают некоторую допустимую точку X[1,0]. Координаты остальных
q–1вершин комплекса:хi [j,0]=аi +ξi (bi –ai ),I=1,2,...,n;j=2,...,q. Здесьаi ,bi – соответственно нижнее и верхнее ограни-
чения на переменную хi ,ξi – псевдослучайные числа, равномерно распределенные на интервале [0;1]. Полученные таким образом
точки удовлетворяют ограничениям аi ≤хi ≤ bi , однако ограниче-
ния zj (X)≤0 могут быть нарушены. В этом случае недопустимая точка заменяется новой, лежащей в середине отрезка, соединяющего недопустимую точку с центром тяжести выбранных допустимых вершин. Данная операция повторяется до тех пор, пока не будут выполнены все ограничения задачи.
2.Далее, как и в методе деформируемого многогранника, на каждой итерации заменяется вершина X[h,k], в которой значение целевой функции имеет наибольшую величину. Для этого она отражается относительно центра тяжестиX[n+2,k] остальных вершин комплекса. ТочкаX[n+3,k], заменяющая вершинуX[h,k], определяется по формулеX[n+3,k]=(a+1)X[n+2,k]+aX[h,k], гдеа>0
–некоторая константа, называемая коэффициентом отражения. Наиболее удовлетворительные результаты дает значение а=1,3. При этом новые вершины комплекса отыскиваются за небольшое количество шагов, а значения целевой функции уменьшаются достаточно быстро.
3.Если f(X[n+3,k])≥f(X[h,k]), то новая вершина оказывается худшей вершиной комплекса. В этом случае коэффициента уменьшается в два раза. Аналогично поступают, если при отраже-
нии нарушаются ограничения zj (X)≤0, до тех пор, пока точкаX[n+3,k] не станет допустимой.
Вычисления заканчиваются, если значения целевой функции в центре тяжести комплекса мало меняются в течение пяти после-
довательных итераций: | f(X[n+2,k+1])–f(X[n+2,k])|≤ε,k=1,2....,5,
где ε – заданная константа. В этом случае центр тяжести комплекса считают решением задачи.
Достоинства комплексного метода Бокса: его простота, удобство для программирования, надежность в работе. Метод на каждом шаге использует информацию только о значениях целевой функции и функций ограничений задачи. Все это обусловливает успешное применение его для решения различных задач нелинейного программирования.
studfiles.net
7.5. Методы условной многокритериальной оптимизации
После нахождения множества Парето, если количество точек в нём  , встаёт вопрос о выборе единственного решения.. Так как точки на множестве Парето обладают свойством, что каждая из них лучше по одному критерию, но хуже по другому, то объективно предпочесть эти точки невозможно.Условная оптимизацияпредполагает введение условия согласованности в компонентах критерия, которое всегда является хотя и разумным, но субъективным. Подобные условия еще называют схемой компромиссов. Рассмотрим несколько простейших из них.
, встаёт вопрос о выборе единственного решения.. Так как точки на множестве Парето обладают свойством, что каждая из них лучше по одному критерию, но хуже по другому, то объективно предпочесть эти точки невозможно.Условная оптимизацияпредполагает введение условия согласованности в компонентах критерия, которое всегда является хотя и разумным, но субъективным. Подобные условия еще называют схемой компромиссов. Рассмотрим несколько простейших из них.
Принцип равенства критериев. Рассматривают множество Парето для стандартных критериев. Тогда оптимальной считается та точка множеств Парето, гдеk1=k2=…=kL(см. рисунок).
П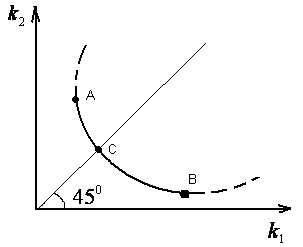 ринцип равного влияния. Здесь оптимальной считается точка множества Парето, являющаяся точкой касания прямойk1 +k2minи области Парето (точка С, см. рисунок)
ринцип равного влияния. Здесь оптимальной считается точка множества Парето, являющаяся точкой касания прямойk1 +k2minи области Парето (точка С, см. рисунок)
Принцип минимакса. Оптимальной считается точка множества Парето, где обеспечиваетсяminmaxkiст. (см. рисунок).
Кроме указанных простейших приемов применяются более сложные. 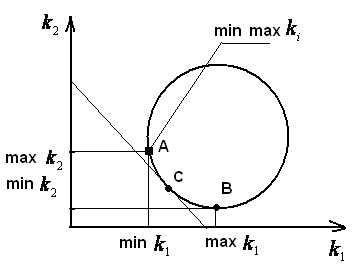
1) Метод скаляризации. Здесь формируется некоторая скалярная функция многих переменных:
K0- это скалярная величина, которая обобщает все критерии. Наиболее распространённой разновидностью функцииfявляется линейная функция
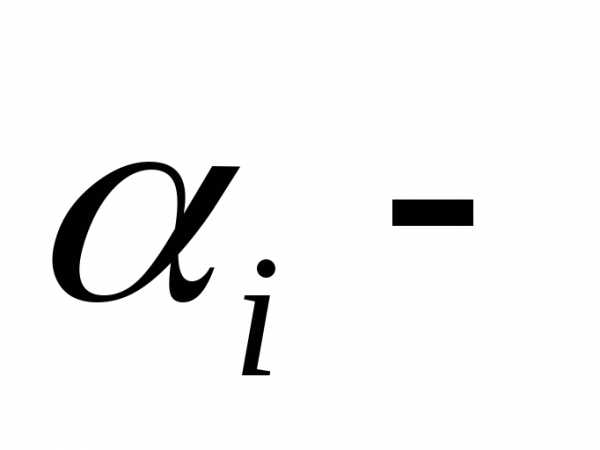 вес каждой компоненты критерия, чем эта величина больше, тем большее влияние оказывает этот критерий. Для нестандартных критериев веса могут иметь размерность, причем если Ki→max, то
вес каждой компоненты критерия, чем эта величина больше, тем большее влияние оказывает этот критерий. Для нестандартных критериев веса могут иметь размерность, причем если Ki→max, то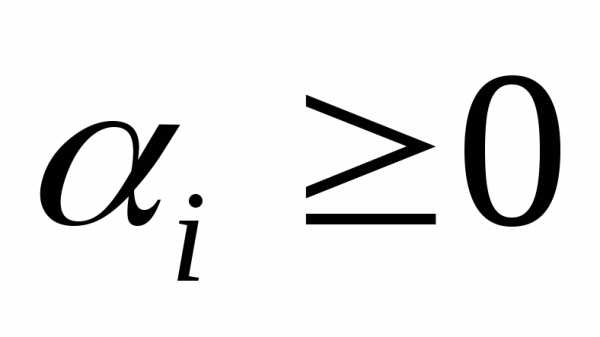 , а когда Ki→min, то
, а когда Ki→min, то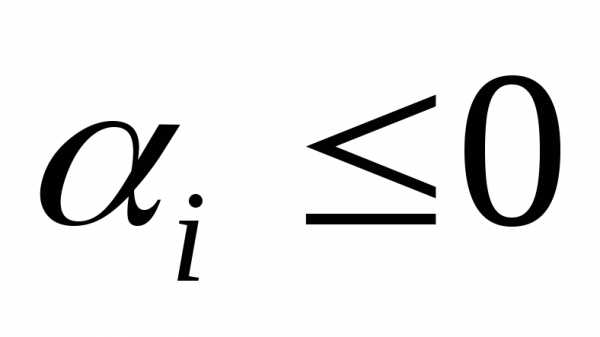 . Подобная комплексная оценка зачастую затруднительна. На практике часто используют и другие способы искусственно объединить несколько показателей в один обобщённый показатель ( критерий). В качестве обобщённого критерия, например, берут дробь:
. Подобная комплексная оценка зачастую затруднительна. На практике часто используют и другие способы искусственно объединить несколько показателей в один обобщённый показатель ( критерий). В качестве обобщённого критерия, например, берут дробь:
K 0= (k1хk2х...km)/(km+1х….kL, )
где k1...km– увеличиваются
km+1..kL- уменьшаются
Вольное использование подобных критериев чревато опасностями и может привести к неправильным рекомендациям.
Общим недостатком «составных критериев» является то, что недостаток эффективности по одному показателю всегда можно скомпенсировать за счёт другого (например, малую вероятность выполнения боевой задачи – за счёт малого расхода боеприпасов и т.п.)
На этот счет известна шутка Л.Н.Толстого, что если представить оценку человека в виде дроби:
то можно получить самую высокую оценку в случае 
2).Метод главного критерия. В этом методе сначала выбирают главный критерий и объявляют его единственным критерием. Все остальные критерии становятся управляемыми переменными, на которые накладываются ограничения, что бы они были не хуже заданной величиныki0. Например, если всеkiminи главныйk1, то получаем однокритериальную задачу математического программирования
k1 = f ( X) –> min
Фi (X) < 0, i = 1,2,3,…m
k2 (X)<k20 , k3(X)<k30 , … , kL(X)<kL0 .
Тогда, эти ограничения войдут в комплекс заданных условий .
Например, в промышленности можно потребовать, что бы прибыль
–> max, план по ассортименту – выполнен, а себестоимость – не выше заданной.
При бомбардировке – понесённый ущерб противника – максимальный, потери и стоимость операции не выходили за известные пределы.
Здесь все показатели эффективности, кроме одного, переводятся в разряд ограничений. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются как недопустимые.
Такой метод чаще всего используется при оптимизации сложных технических систем (самолетов, автомобилей, бытовой техники и т.д.).
3). Метод последовательных уступок. Проранжируем все критерии и расположим их в порядке убывающей важности:k1,k2 ….kL.. Пусть все критерии нужно максимизировать. Сначала отбросим все критерии кромеk1 и найдем допустимое решение, обращающее в максимумk1 . Как правило при этом другие критерии не получают своих наилучших значений. Поэтому исходя из практических соображений и точности, с какой известны исходные данные назначается уступка ⌂k1, которую мы согласны допустить для того, чтобы обратить в максимумk2 . Наложим наk1 ограничение, чтобы он был не меньше чемk1*- ⌂k1 (k1*- максимально возможное значениеk1 )и при этом ограничении ищем решение, обращающее в максимумk2 . Далее снова назначается уступка в показателеk2 ценой, которой находится максимумk3и т.п.
На втором этапе решаем задачу
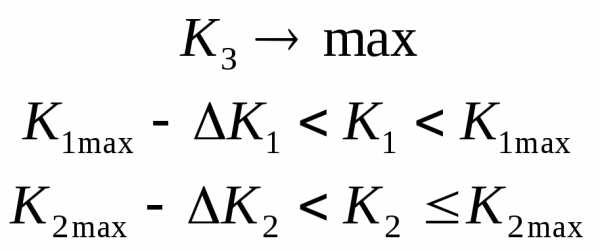
И так далее.
Такой способ хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом. Заметим , что иногда даже при малом ⌂k«свобода» выбора позволяет достичь существенной оптимизацииk2 . Это зависит от вида границы критериального пространства. (см. рисунок).
Очевидно, успех такого метода зависит от того, насколько «тупой» максимум. Процедура может быть повторена для других 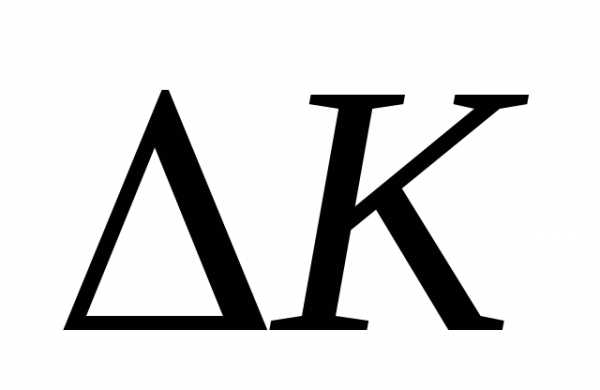 .
.
4. Метод последовательной оптимизации. В некоторых случаях критерии системы не слишком связаны друг с другом, т.е. улучшение одного критерия по крайней мере в ограниченных пределах не «мешает» другому. Это характерно для сложных систем, состоящих из отдельных достаточно автономных подсистем, (например: процессор компьютера, система электропитания, система охлаждения, система отображения), когда отдельные критерии относятся к этим подсистемам. Расположим все критерии в порядке убывания важности. Сначала оптимизируют систему по важнейшему показателю, отбросив все остальные, затем по второму, и т. д.
Следует отметить, что в вышеприведенных методах используется процедура упорядочения критериев по важности. Эта самостоятельная проблема является достаточно сложной и поэтому решается на основе методов экспертных оценок, изложенных в 10 главе.
studfiles.net