Одномерная оптимизация Методы дихотомии золотого сечения Ньютона секущих. Методы оптимизации метод ньютона
Одномерная оптимизация Методы дихотомии золотого сечения Ньютона секущих
 Одномерная оптимизация. Методы дихотомии, золотого сечения, Ньютона, секущих.
Одномерная оптимизация. Методы дихотомии, золотого сечения, Ньютона, секущих.
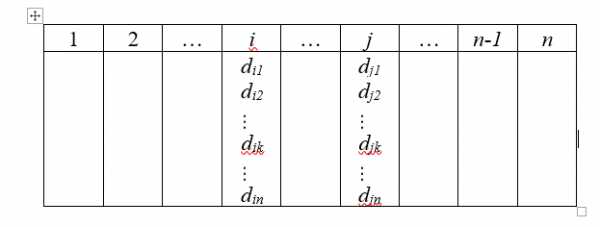
 Оптимизация (от лат. «optimus» -наилучший) – поиск наилучшего варианта, при наличии множества альтернативных. Задача для решения методом оптимизации состоит в минимизации вещественнозначной функции f(x) N-ного аргумента x, компоненты которого удовлетворяют системе ограничений в виде уравнений Hk(x)=0, k=1, 2, …, m или неравенств gj(x)≥ 0, j=m+1, …s. Задачи без ограничений с N=1 называются задачами одномерной оптимизации
Оптимизация (от лат. «optimus» -наилучший) – поиск наилучшего варианта, при наличии множества альтернативных. Задача для решения методом оптимизации состоит в минимизации вещественнозначной функции f(x) N-ного аргумента x, компоненты которого удовлетворяют системе ограничений в виде уравнений Hk(x)=0, k=1, 2, …, m или неравенств gj(x)≥ 0, j=m+1, …s. Задачи без ограничений с N=1 называются задачами одномерной оптимизации
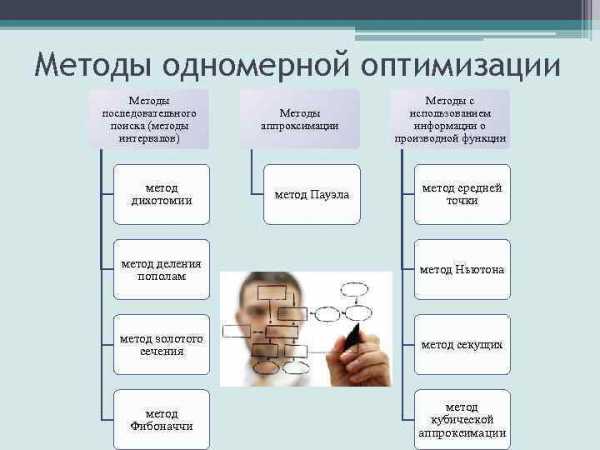 Методы одномерной оптимизации Методы последовательного поиска (методы интервалов) метод дихотомии Методы аппроксимации метод Пауэла Методы с использованием информации о производной функции метод средней точки метод деления пополам метод Ньютона метод золотого сечения метод секущих метод Фибоначчи метод кубической аппроксимации
Методы одномерной оптимизации Методы последовательного поиска (методы интервалов) метод дихотомии Методы аппроксимации метод Пауэла Методы с использованием информации о производной функции метод средней точки метод деления пополам метод Ньютона метод золотого сечения метод секущих метод Фибоначчи метод кубической аппроксимации
 Метод золотого сечения • Отрезок AB разделен точкой D в пропорции золотого сечения, если отношение всей длины отрезка к длине большей его части равно отношению длины большей его части к длине меньшей, т. е. • Пусть длина AB = 1, а AD = x. Тогда, откуда x =. Понятно, что больший отрезок можно было бы отложить не от левого, а от правого конца отрезка. Тогда получили бы точку золотого сечения C, симметричную т. D относительно центра, и AC =. Точку C называют первой, а D второй точкой золотого сечения. Эти точки обладают замечательными свойствами. • Рисунок - Первая и вторая точка золотого сечения
Метод золотого сечения • Отрезок AB разделен точкой D в пропорции золотого сечения, если отношение всей длины отрезка к длине большей его части равно отношению длины большей его части к длине меньшей, т. е. • Пусть длина AB = 1, а AD = x. Тогда, откуда x =. Понятно, что больший отрезок можно было бы отложить не от левого, а от правого конца отрезка. Тогда получили бы точку золотого сечения C, симметричную т. D относительно центра, и AC =. Точку C называют первой, а D второй точкой золотого сечения. Эти точки обладают замечательными свойствами. • Рисунок - Первая и вторая точка золотого сечения
 Алгоритм • На первой итерации принимаем a 1 = a, b 1 = b и вычисляем c 1 = , d 1 =. • Далее, получив значения функции f в точках c 1 и d 1 , сравниваем их. ØЕсли f(c 1) ≤ f(d 1), то a 2 = a 1 , b 2 = d 1 , d 2 = c 1 , c 2 = ØЕсли же f(c 1) > f(d 1), то a 2 = c 1 , b 2 = b 1 , c 2 = d 1 , d 2 =.
Алгоритм • На первой итерации принимаем a 1 = a, b 1 = b и вычисляем c 1 = , d 1 =. • Далее, получив значения функции f в точках c 1 и d 1 , сравниваем их. ØЕсли f(c 1) ≤ f(d 1), то a 2 = a 1 , b 2 = d 1 , d 2 = c 1 , c 2 = ØЕсли же f(c 1) > f(d 1), то a 2 = c 1 , b 2 = b 1 , c 2 = d 1 , d 2 =.
 • Далее сравниваем f(c 2) с f(d 2), определяя новые значения a 3 , b 3 , и т. д. до тех пор, пока не выполнится , где требуемая точность. • На каждой итерации длина локализующего отрезка уменьшается в раз, следовательно (b – a).
• Далее сравниваем f(c 2) с f(d 2), определяя новые значения a 3 , b 3 , и т. д. до тех пор, пока не выполнится , где требуемая точность. • На каждой итерации длина локализующего отрезка уменьшается в раз, следовательно (b – a).
 Пример расчёта методом золотого сечения Рассмотрим функцию , a = 0. 5, b = 3. 5 и найдем точку минимума с погрешностью ε=0. 5. 1) a 1 = 0. 5, b 1 = 3. 5, 2) a 2 = a 1 = 0. 5, b 2 = d 1 = 2. 354, d 2 = c 1 = 1. 646, поэтому продолжаем
Пример расчёта методом золотого сечения Рассмотрим функцию , a = 0. 5, b = 3. 5 и найдем точку минимума с погрешностью ε=0. 5. 1) a 1 = 0. 5, b 1 = 3. 5, 2) a 2 = a 1 = 0. 5, b 2 = d 1 = 2. 354, d 2 = c 1 = 1. 646, поэтому продолжаем
 3) a 3 = c 2 = 1. 208, b 3 = b 2 = 2. 354, c 3 = d 2 = 1. 646, поэтому продолжаем 4) a 4 = a 3 = 1. 208, b 4 = d 3 = 1. 916, d 4 = c 3 = 1. 646, т. е. это последняя итерация Принимаем хm=
3) a 3 = c 2 = 1. 208, b 3 = b 2 = 2. 354, c 3 = d 2 = 1. 646, поэтому продолжаем 4) a 4 = a 3 = 1. 208, b 4 = d 3 = 1. 916, d 4 = c 3 = 1. 646, т. е. это последняя итерация Принимаем хm=
present5.com
1. Метод Ньютона и его модификации
1.1. Метод Ньютона
Предположим, функция f выпукла и дважды дифференцируема на Rn, причем матрица f’’(x) невырождена на Rn. В методе Ньютона последовательность x0, x1, x2,… генерируется исходя из следующих соображений.
По определению дважды дифференцируемой функции для очередной точки xk имеем
. (1.1)
Для определения следующей точки xk+1 минимизируется функция fk(x), является квадратичной частью приращения f(x)-f(xk), т.е. решается задача
. (1.2)
Ясно, что fk’’(x)=f’’(xk) . Так как необходимым и достаточным условием выпуклости функции является неотрицательная определенность матрицы ее вторых производных, а функция f выпукла по условию, то функция fk выпукла. Поэтому необходимое и достаточное условие имеет вид
. (1.3)
Решая полученную систему линейных уравнений и принимая найденную точку минимума за xk+1, получаем
. (1.4)
Данное соотношение определяет метод Ньютона минимизации функции f, совпадающий, как нетрудно увидеть методом Ньютона для решения системы уравнений f’(x)=0.
Исследуем сходимость метода.
1.2. Сходимость метода Ньютона и оценка скорости сходимости
Теорема. Пусть функция f дважды дифференцируема, сильно выпукла с константой θ>0 на Rn и удовлетворяет условию
, (1.5)
где М>0, а начальная точка x0 такова, что , т.е.
. (1.6)
Тогда последовательность 1.1 сходится к точке минимума х* с квадратичной скоростью:
. (1.7)
Доказательство. Точка минимума х* существует и единственна. Условие сильной выпуклости эквивалентно следующему:
. (1.8)
Отсюда следует, что матрица f’’(x) положительно определенна и потому невырождена при всех xRn . Таким образом, метод 1.1 определен корректно.
Учитывая, что f’(x*)=0, получаем
, (1.9)
т.е.
. (1.10)
Оценим величину Интегрируя поt от 0 до 1 соотношение
. (1.11)
И вычитая с обеих частей полученного равенства , имеем
, (1.12)
Откуда, в силу 1.2 имеем
. (1.13)
Подставляя сюда , приходим к неравенству
. (1.14)
Оценим теперь величину . Полагаяполучаем из 1.4
(1.15)
откуда
. (1.16)
С учетом полученной оценки из 1.6 следует, что
. (1.17)
Это неравенство справедливо при всех х поэтому, используя 1.3, получаем
. (1.18)
Утверждение теоремы теперь непосредственно следует из 1.5.
Таким образом, сходимость метода Ньютона доказана лишь дл достаточно хорошего начального приближения х0. При этом условие 1.3, гарантирующее сходимость для данного приближения, труднопроверяемо, так как фигурирующие в нем константы, как правило, неизвестны.
Сложность отыскания нужного начального приближения является недостатком метода Ньютона. Еще более существенным недостатком является трудоемкость метода, обусловленная необходимостью вычисления и обращения на каждом шаге матрицы вторых производных минимизируемой функции.
В силу названных причин применение классического метода Ньютона далеко не всегда приводит к успеху. Многочисленные модификации направлены на то, чтобы, сохраняя основное достоинство метода Ньютона – его быструю сходимость, уменьшить трудоемкость и ослабить требования на выбор начального приближения.
studfiles.net
Метод Ньютона.
Метод Ньютона относится к методам 2-го порядка и рекомендуется с применению в том случае, когда задача минимизации достаточно хорошо локализована.
Обычно это имеет место в том случае, когда на начальном этапе применяется один из методов 0-го порядка, а затем осуществляется переход к методу Ньютона. Для этого необходимым условием является гладкость , существование не равных нулю , , для .
Тогда если -k-е приближение к точке минимума, то расчетной формулой метода Ньютона будет формула
.
Метод Ньютона имеет высокую скорость сходимости:
где  - точка минимума;С - некоторая положительная константа.
- точка минимума;С - некоторая положительная константа.
Процесс вычисления продолжается до тех пор, пока не будет достигнуто
На следующем рисунке приведена блок-схема алгоритма.
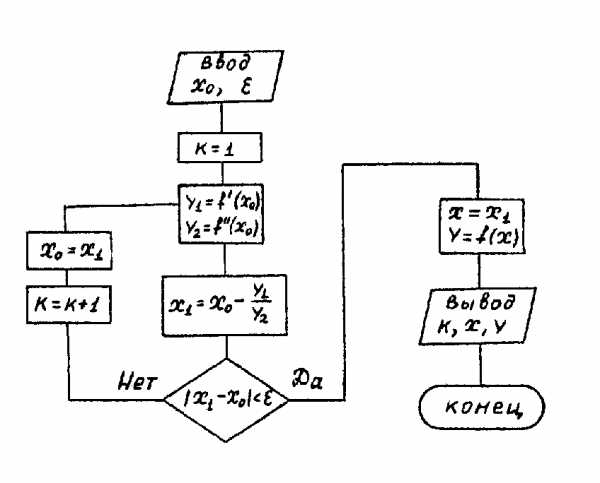
Рисунок 3.3.14
Блок - схема метода Ньютона.
Пример.
Найти минимум на отрезке c точностью.
Зададимся , например, возьмем середину отрезка :
Пусть
Для данного примера расчетной формулой метода Ньютона будет
1-й шаг.
2й шаг.
Решение.
Замечание.
Число сохраняемых знаков после округления определяется заданной точностью .
Численные методы минимизации многоэкстремальных функций.
До сих пор рассматривались унимодальные функции, имеющие на отрезке единственную точку минимума. Если функция на отрезке многоэкстремальна (то есть существует несколько минимумов функции ), то возникает задача отыскания глобального минимума функции .
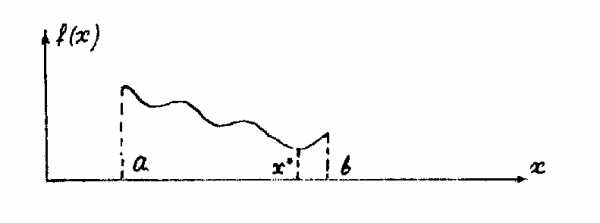
Рисунок 3.4.15
Рисунок 3.4 .15 - пример такой функции, где - точка глобального минимума.
Ограничимся рассмотрением функций, удовлетворяющих условию Липшица на отрезке :
,
где M - константа Липшица.
Существует несколько методов определения глобального минимума таких функций. Остановимся на двух из них: методе перебора и методе ломаных.
Метод перебора.
Суть метода перебора состоит в следующем:
в точках отрезка
, 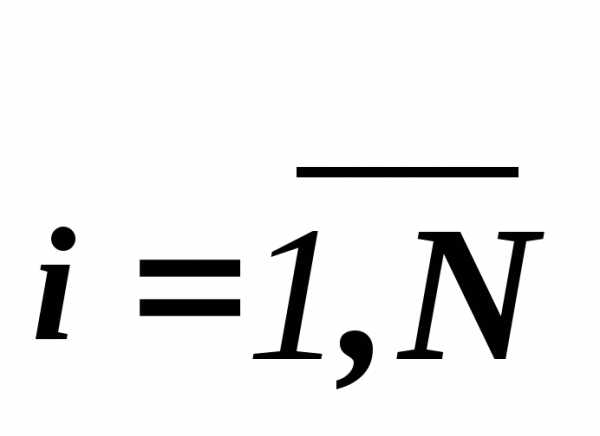
вычисляются значения функции и в качестве минимального значения принимается значение
.
Погрешность метода не превосходит величины. Это легко показать, так как если точка глобального минимума, то очевидно, найдется такая точка
точка глобального минимума, то очевидно, найдется такая точка 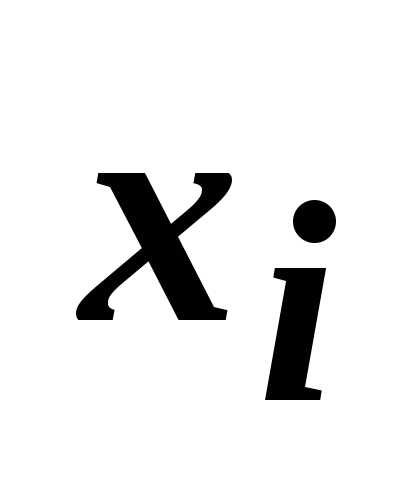 ,, что
,, что
Тогда с учетом условия Липшица
Таким образом, задаваясь необходимой величиной погрешности можно определить требуемое количество точекна отрезке :
Блок-схема метода перебора приведена ниже.
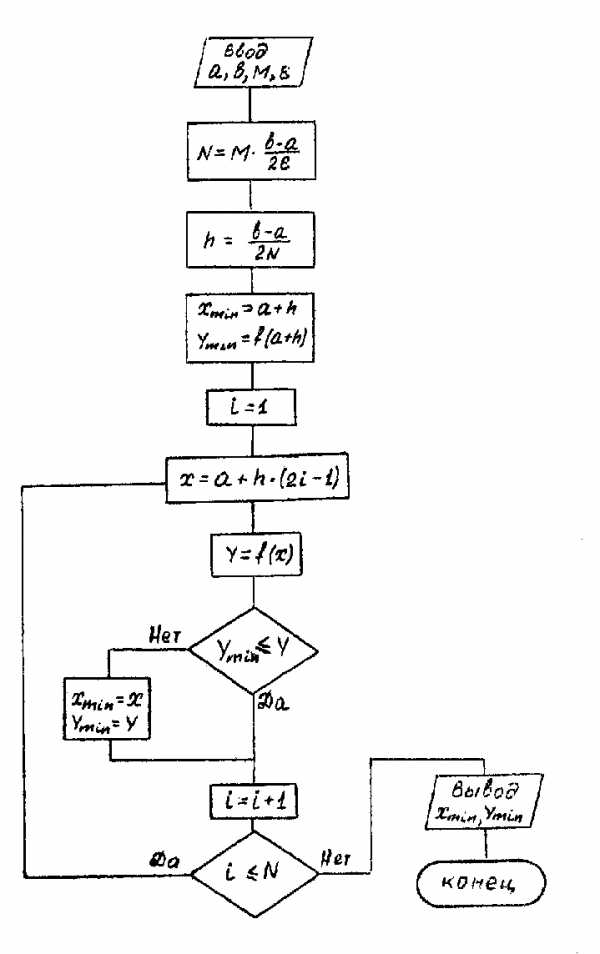
Рисунок 3.4.16
Метод ломаных.
На отрезке выбирают точек
В каждой точке вычисляется значение функции и строится миноранта
для функции, представляющая собой ломаную:
определяется точка x, в которой достигает минимума, и она принимается в качестве дополнительнойточки для исследования функции на минимум
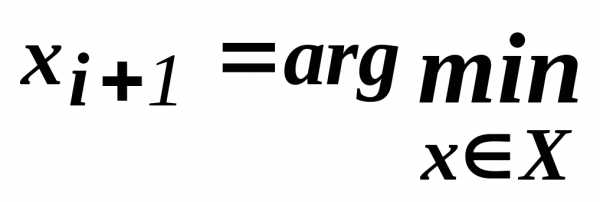 .
.
С введением точки минорантапреобразуется в минорантуи далее процесс введения следующей точки повторяется.
В качестве приближения к искомому значению минимума после вычислений значений функции принимается величина
.
Очевидно, что погрешность метода не превосходит величины
- .
Значение может быть задано или же будет определяться, исходя из требуемой точностивычисления значения минимума функции . Во втором случае вычисления прекращаются как только
-
Рисунок 3.4 .17 - Рисунок 3.4 .20 иллюстрируют применение метода ломаных для определения глобального минимума функции . Проведено четыре итерации.
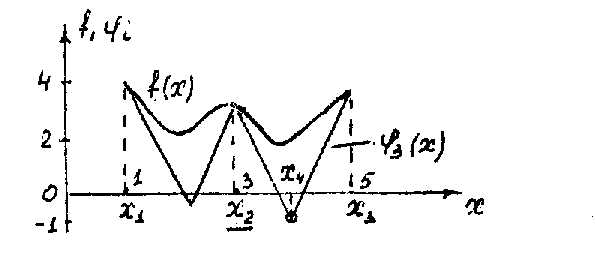
Рисунок 3.4.17
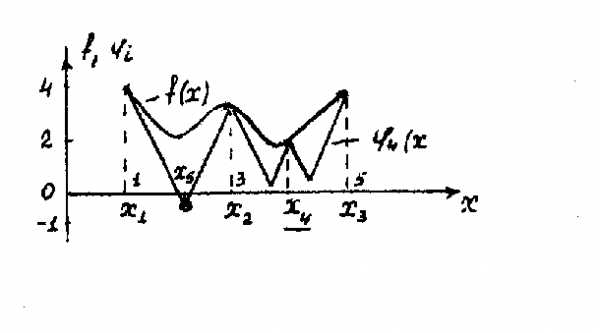
Рисунок 3.4.18
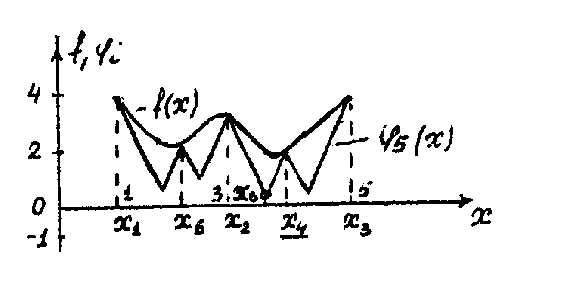
Рисунок 3.4.19
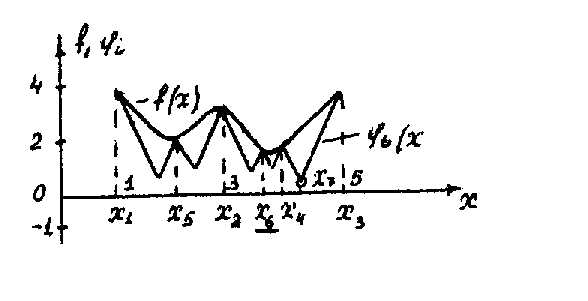
Рисунок 3.4.20
При реализации обоих методов требуется знать значение константы Липшица . На практике значение часто неизвестно. В этом случае в качестве можно использовать оценку
,
где
,
studfiles.net
3.3. Методы второго порядка
Методы прямого поиска и градиентные методы являются достаточно эффективными только на начальном этапе минимизации. На последующих этапах, когда поисковые точки находятся вблизи точки минимума , необходимо применять методы, имеющие более высокую скорость сходимости. Важнейший класс методов такого типа составляют методы второго порядка, к которым относятся метод Ньютона и связанные с ним квазиньютоновские методы. Они позволяют учитывать структуру целевой функции.
3.3.1. Метод Ньютона
Пусть функция 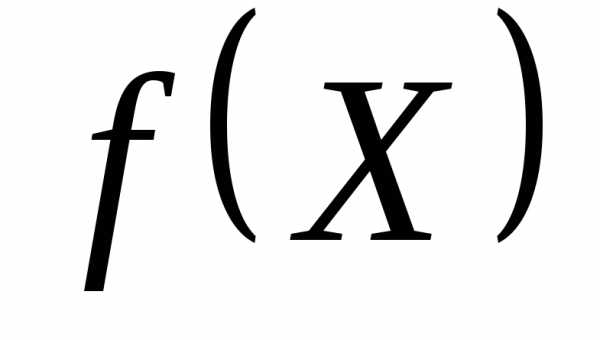 дважды непрерывно дифференцируема и
дважды непрерывно дифференцируема и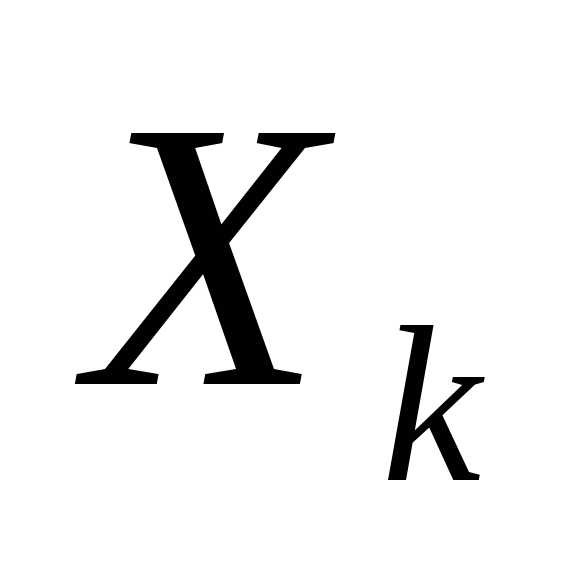 - некоторая точка пространства поиска. Из курса математического анализа известно, что дважды непрерывно дифференцируемую функцию в достаточно малой окрестности точки
- некоторая точка пространства поиска. Из курса математического анализа известно, что дважды непрерывно дифференцируемую функцию в достаточно малой окрестности точки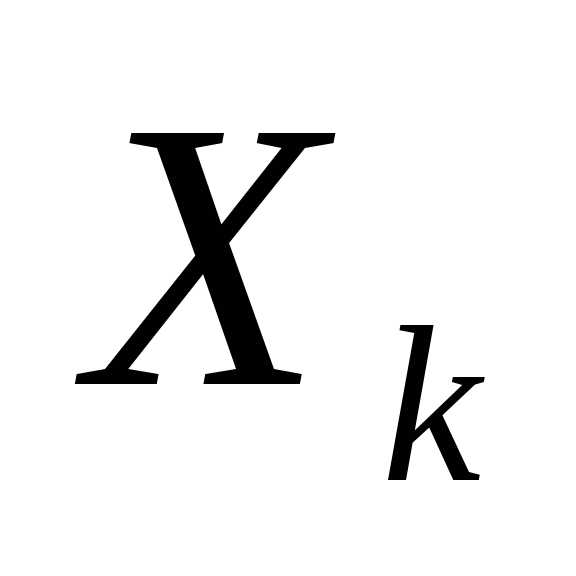
где 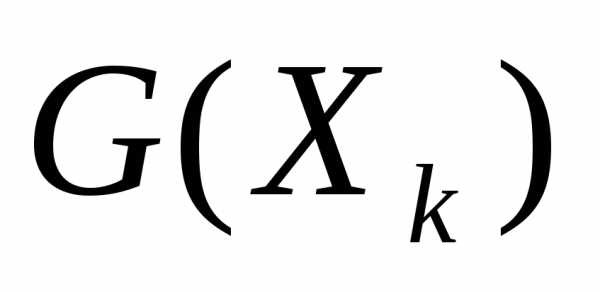 - матрица Гессе.
- матрица Гессе.
Если функция 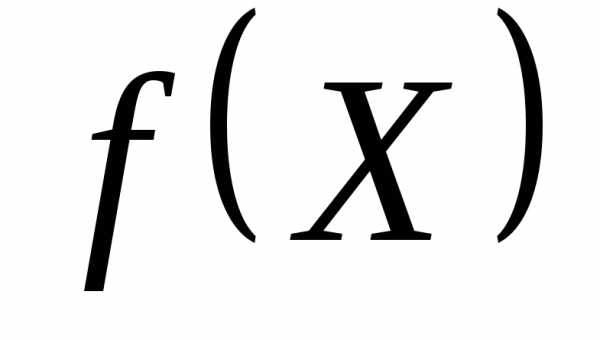 в некоторой точке
в некоторой точке  имеет минимум, то в этой точке.
имеет минимум, то в этой точке.
Отсюда следует, что если матрица 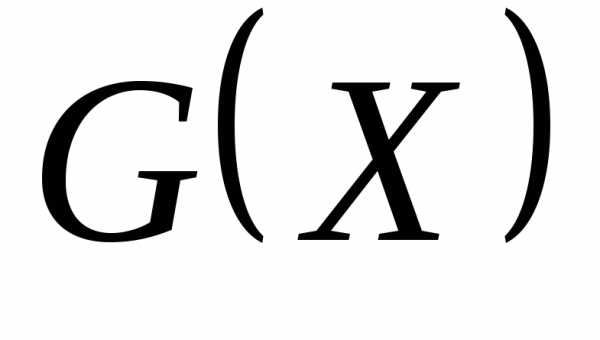 имеет обратную, то точкуможно найти по формуле
имеет обратную, то точкуможно найти по формуле
.
Повторяя эту процедуру, получим рекуррентную формулу метода Ньютона:
,
В задачах поиска минимума произвольной квадратичной функции с положительной матрицей вторых производных, метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки. В общем случае метод Ньютона может расходиться, если начальное приближение находится вдали от точки минимума. Сходимость метода Ньютона можно гарантировать только в тех случаях, когда начальное приближение находится в достаточно малой окрестности точки минимума и матрица Гессе положительно определена и хорошо обусловлена. Поэтому на практике этот метод обычно используется в сочетании с одним из методов, быстро сходящимся вдали от точки минимума.
Важнейшим обобщением метода Ньютона является метод Ньютона с регулировкой шага. Последовательность итераций строится в соответствии с формулой
,
Выбор 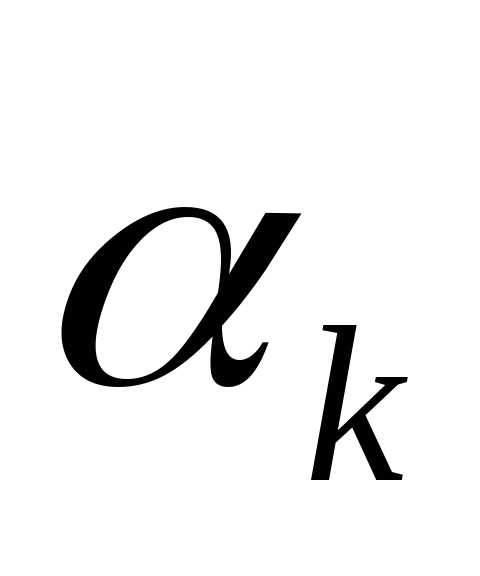 осуществляется таким образом, чтобы. Эта модификация метода Ньютона оказывается надежной и эффективной. Тем не менее на каждой итерации надо обращать матрицу Гессе, для чего требуется большой объем памяти ЭВМ.
осуществляется таким образом, чтобы. Эта модификация метода Ньютона оказывается надежной и эффективной. Тем не менее на каждой итерации надо обращать матрицу Гессе, для чего требуется большой объем памяти ЭВМ.
Для устранения этих недостатков были разработаны квазиньютоновские методы, использующие ньютоновские направления по мере возможности и уклоняющиеся от них только тогда, когда это необходимо. Самым широко используемым является метод Дэвидона - Флетчера - Пауэлла.
Пример. Щелкнув по значку, откроется Mathcad документ метода Ньютона, в котором можно выполнить вычисления.
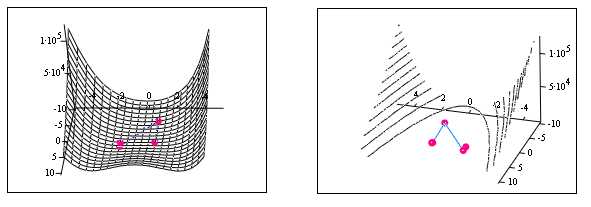
Минимизация функции
методом Ньютона
3.3.2.Метод Дэвидона - Флетчера - Пауэлла
Первоначально метод был предложен Дэвидоном и затем развит Флетчером и Пауэллом. Метод Дэвидона-Флетчера-Пауэлла называют также и методом переменной метрики. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска на 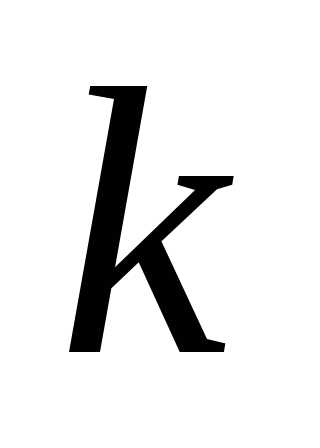 -той итерации задаются в виде. Направление градиента является, таким образом, отклоненным в результате умножения на
-той итерации задаются в виде. Направление градиента является, таким образом, отклоненным в результате умножения на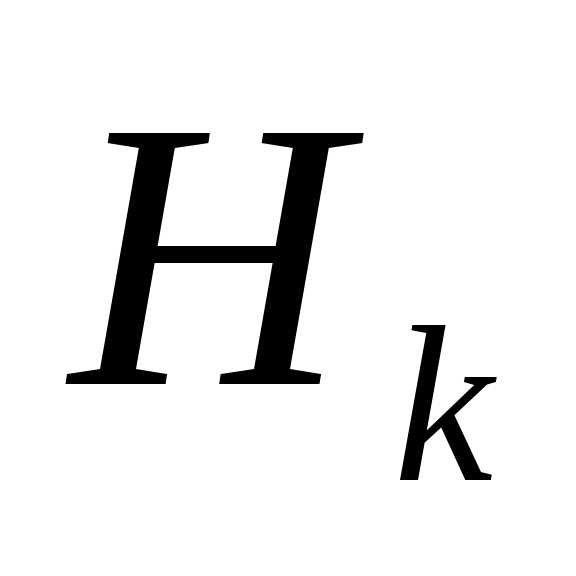 , где
, где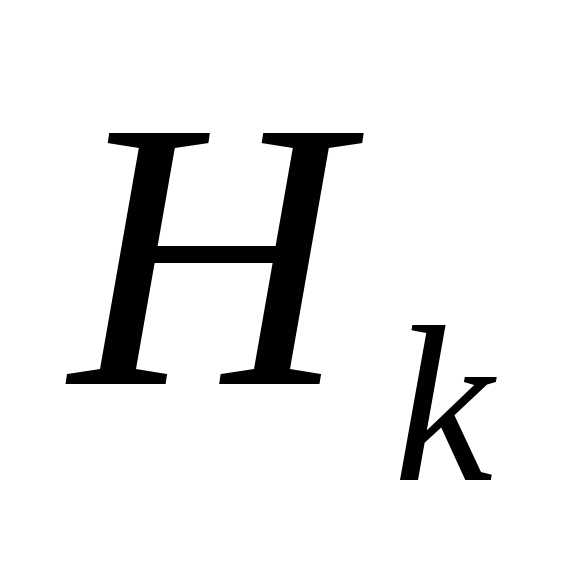 - положительно определенная симметрическая матрица порядка
- положительно определенная симметрическая матрица порядка  , аппроксимирующая обратную матрицу Гессе. На каждом шаге матрица
, аппроксимирующая обратную матрицу Гессе. На каждом шаге матрица 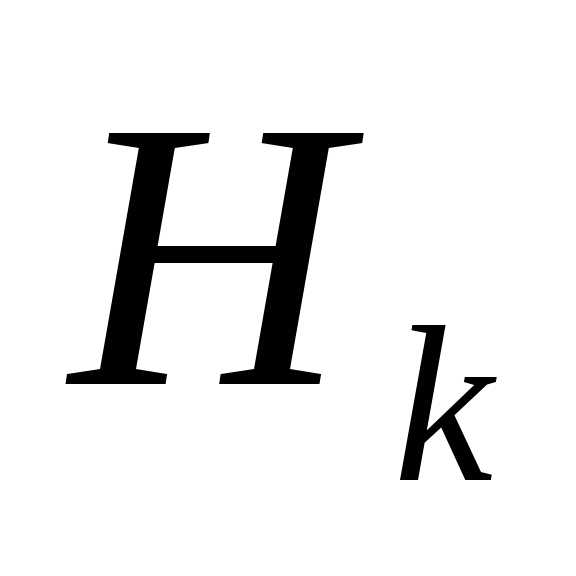 обновляется, т.е. представляется в виде
обновляется, т.е. представляется в виде
,
где
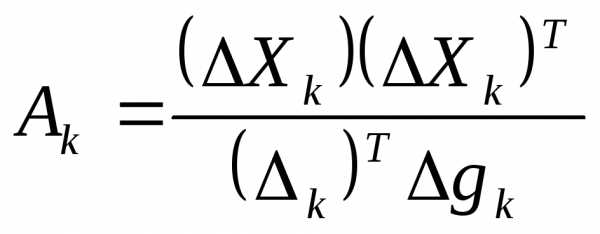 ; (1)
; (1)
; (2)
; (3)
. (4)
Следует отметить, что 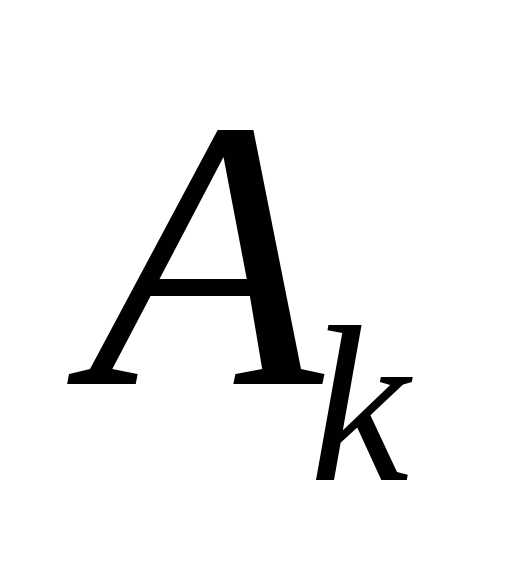 и
и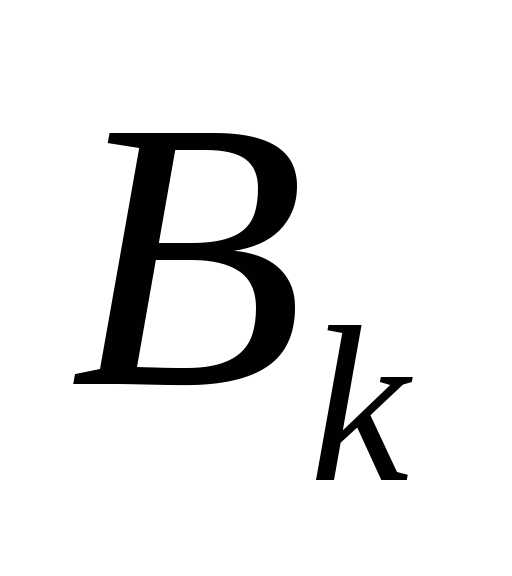 - симметричные матрицы, следовательно,
- симметричные матрицы, следовательно,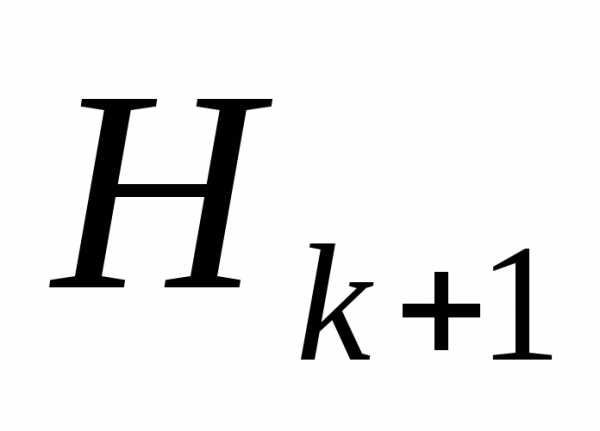 - симметричная и положительно определенная матрица. Матрица
- симметричная и положительно определенная матрица. Матрица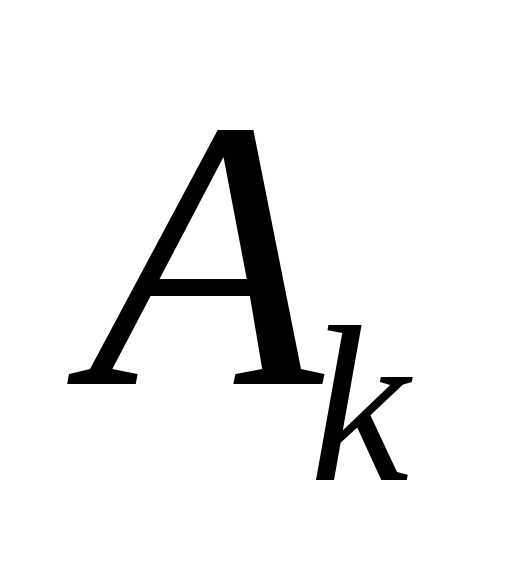 обеспечивает сходимость
обеспечивает сходимость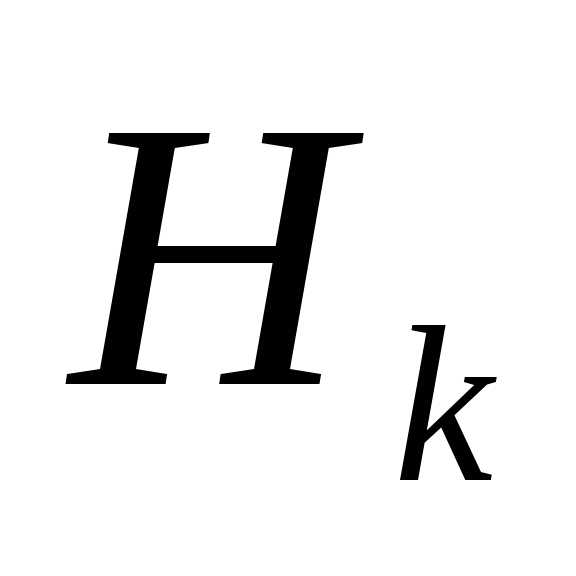 к
к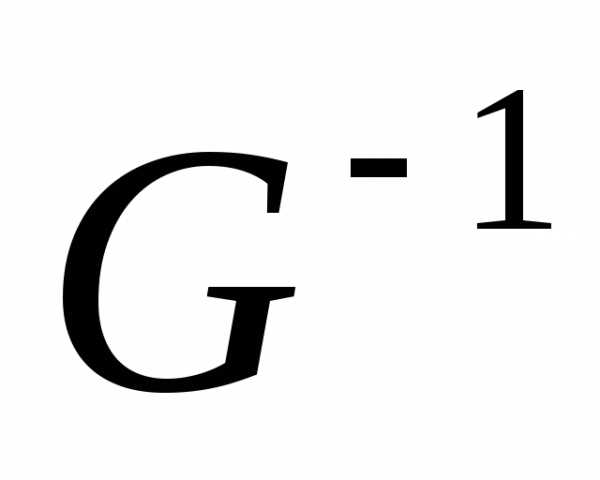 ; матрица
; матрица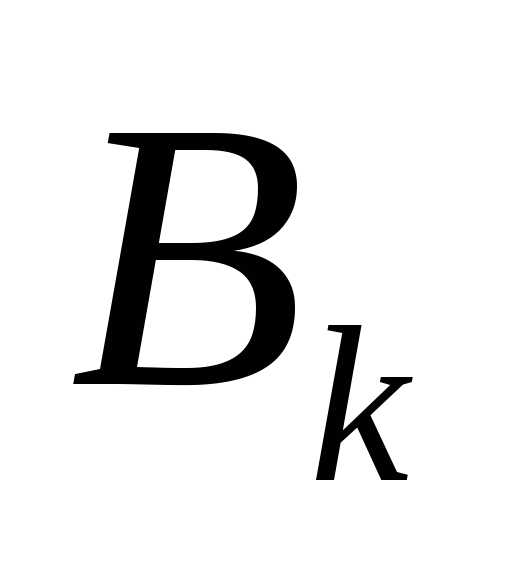 обеспечивает положительную определенность
обеспечивает положительную определенность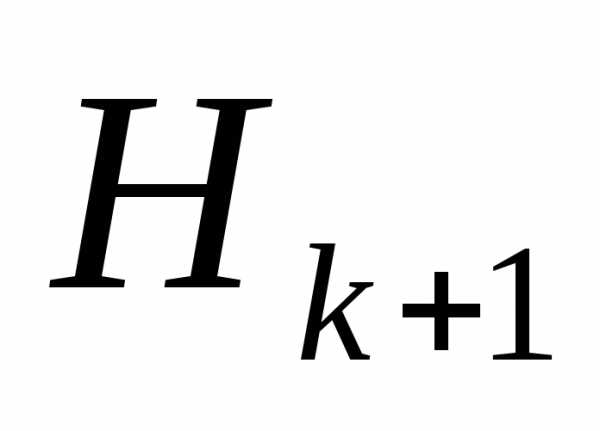 на всех этапах и на конечном этапе исключает начальную
на всех этапах и на конечном этапе исключает начальную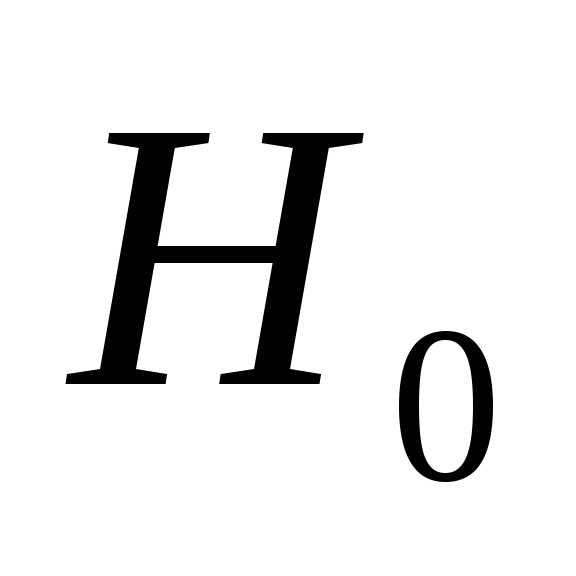 . В качестве
. В качестве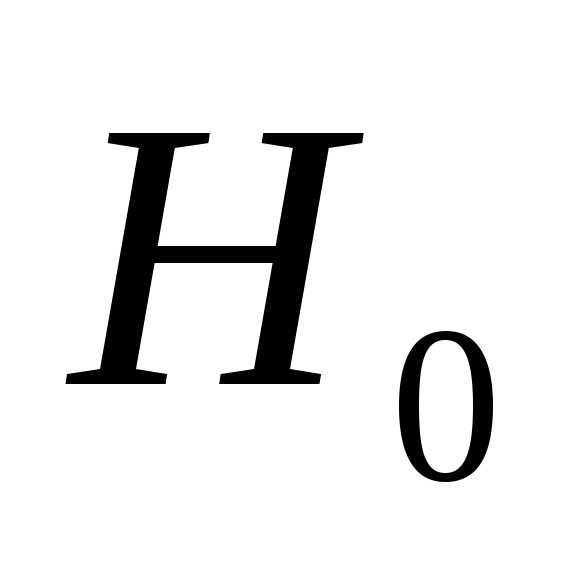 можно выбрать единичную.
можно выбрать единичную.
studfiles.net
Численные методы безусловной оптимизации Метод Ньютона Историческая
 Численные методы безусловной оптимизации. Метод Ньютона
Численные методы безусловной оптимизации. Метод Ньютона
 Историческая справка Метод Ньютона был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» , адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» или «Аналитическая геометрия» в собраниях трудов Ньютона, которая была написана в 1671 году. Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году
Историческая справка Метод Ньютона был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» , адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» или «Аналитическая геометрия» в собраниях трудов Ньютона, которая была написана в 1671 году. Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году
 Применение: для нахождения корней функции f(x) = 0 Алгоритм: Дано уравнение f(x)=0 где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)=…=fk-1(ξ)= 0.
Применение: для нахождения корней функции f(x) = 0 Алгоритм: Дано уравнение f(x)=0 где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)=…=fk-1(ξ)= 0.
 Приближенное нахождение корней уравнения I) Отделение корней, то есть установление интервалов [αi, βi], в которых содержится один корень уравнения. 1. f(a) • f(b) 0; x 0 є[a; b] II) Уточнение приближенных корней, то есть доведение их до заданной точности
Приближенное нахождение корней уравнения I) Отделение корней, то есть установление интервалов [αi, βi], в которых содержится один корень уравнения. 1. f(a) • f(b) 0; x 0 є[a; b] II) Уточнение приближенных корней, то есть доведение их до заданной точности
 Пример решения метода Ньютона Дано: (1) Интервал: -1; 1 Точность: ε
Пример решения метода Ньютона Дано: (1) Интервал: -1; 1 Точность: ε
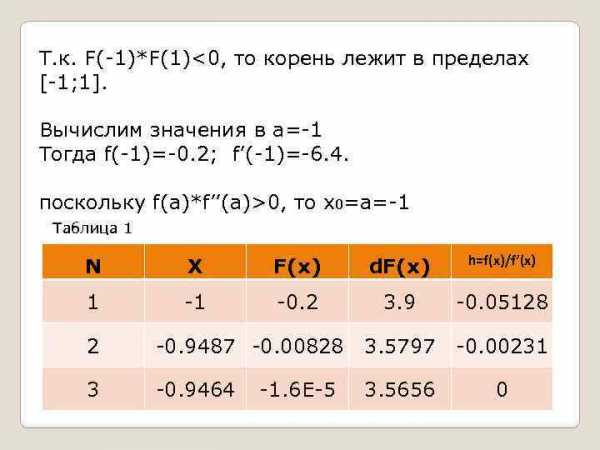 Т. к. F(-1)*F(1)0, то x 0=a=-1 Таблица 1 N X F(x) d. F(x) h=f(x)/f’(x) 1 -1 -0. 2 3. 9 -0. 05128 2 -0. 9487 -0. 00828 3. 5797 -0. 00231 3 -0. 9464 3. 5656 0 -1. 6 E-5
Т. к. F(-1)*F(1)0, то x 0=a=-1 Таблица 1 N X F(x) d. F(x) h=f(x)/f’(x) 1 -1 -0. 2 3. 9 -0. 05128 2 -0. 9487 -0. 00828 3. 5797 -0. 00231 3 -0. 9464 3. 5656 0 -1. 6 E-5
 (5) (6) Ответ: x=-0, 94640472, F(x)= -1. 6 E-5
(5) (6) Ответ: x=-0, 94640472, F(x)= -1. 6 E-5
 Достоинства и недостатки Достоинства Недостатки если минимизируемая функция является квадратичной, то метод позволит найти минимум за один шаг необходимость достаточного начального приближения. если минимизируемая функция относится к классу поверхностей вращения (т. е. обладает симметрией), то метод также обеспечивает сходимость за один шаг медленная скорость сходимости, что приводит к значительным затратам машинного времени при решении сложных нелинейных уравнений если функция несимметрична, то метод не обеспечивает сходимость за конечное число шагов необходимость вычисления производных на каждом шаге
Достоинства и недостатки Достоинства Недостатки если минимизируемая функция является квадратичной, то метод позволит найти минимум за один шаг необходимость достаточного начального приближения. если минимизируемая функция относится к классу поверхностей вращения (т. е. обладает симметрией), то метод также обеспечивает сходимость за один шаг медленная скорость сходимости, что приводит к значительным затратам машинного времени при решении сложных нелинейных уравнений если функция несимметрична, то метод не обеспечивает сходимость за конечное число шагов необходимость вычисления производных на каждом шаге
present5.com
метод Ньютона и его модификации, методы переменной метрики.
Постановка задачи
,, задана функция. Необходимо найтиmin(илиmax)
исходные данные:
Классификация методов:
1) Прямые методы поиска
Знание целевой ф-ии не нужно, необходимо только уметь вычислять ее в точках
2) Методы первого порядка (градиентные методы)
Нужно знать вид функции, уметь вычислять первую производную. Выбор направления основан на вычислении градиента
3) Методы второго порядка
Нужно знать вид функции, уметь вычислять градиент и матрицу Гессе
Метод Ньютона.
1.,k= 0, выч-м–матрица Гессе
2.Вычисляем
3.
4.выч-м
2.Вычисляем
5. Если , то, останов, иначеk=k+1 и переход к шагу 2.
Модификации:
Метод Ньютона-Рафсона(с опт. выбором шага)
, где– минимум ф-ии вдоль направления
Первая модификация метода Ньютона.
Модификация 2 метода Ньютона
Через mитераций вычисляем, т.е. Н не изменяется m итераций, потом вычисляется, потом снова m раз не изменяется и т.д.
10. Задача линейного программирования. Основные определения. Лексикографический вариант прямого симплекс-метода. Вырожденность в задачах линейного программирования. Геометрическая интерпретация симплекс-метода.
Общая форма ЗЛП:
, –целевая ф-ия
–вектор-строка
–вектор-столбец
n–размерность пространства
– ограничения Х
,
кол-во ограничений m
- неотрицательные переменные (остальные- свободные)
– матрица mxn
–вектор-столбец
Основные определения
–столбец
Опр.Любой набор линейно-независимых столбцов (,…,) называется базисом
А=[B,N], где В-матрица, состоящая из линейно-независимых столбцов
N-все остальные.
число базисов
x=,
Опр.Переменные, являющиеся компонентаминазываются базисными переменными
Переменные , не являющиеся компонентаминазываются небазисными переменными
Опр.Решение системыназывается базисным решением.
Каждому базису соответствует базисное решение, но базисное решение может соответсвовать немкольким базисам.
Утв.является базисным решением<=> множество столбцов, которые образуют базис ({}) являются линейно-независимыми.
Опр.Базисным допустимым решением называется любой элемент мн-ва
Утв.является базисно-допустимым решением (бдр) <=> когдаявл. крайней точкой
Опр.Симплекс-таблица называется прямо допустимой, если,i=1..m
Опр.Симплекс-таблица называется двойственно допустимой, если,j=1..n
Утв.Если ЗЛП разрешима, то существует прямо и двойственно допустимая симплекс-таблица
(ЗЛП разрешима, если х не и ф-ия ограничена снизу)
Утв.(достаточное условие оптимальности) если симплекс-таблица явл прямо и двойственно допустимой, то соответствующее базисное решение оптимальное.
Опр.Базисное решение называется вырожденным, если, для которого
Утв.Пусть базисно допустимое решение х невырожденное,,, то тогда существует другое б.д.р., у которого целевая ф-ия меньше
Опр.ЗЛП называется вырожденной, есливырожденное б.д.р.
Утв.В случае невырожденной ЗЛП прямой симплекс-метод является конечным, а если ЗЛП вырожденная, то зацикливание возможно
Лексографический вариант
Опр.Пусть задан вектор=(), тогда векторлексиграфически положительный,если первый отличный от нуля компонент вектора положительный. (0,0,0,1,-1,0…) , т.е. если
Утв.Пусть заданы 2 вектора,, тогда, если.
Если задано множество таких векторов, то среди них всегда можно найти вектор, который будет лексикографическим минимумом : lexmin
Опр.Симплекс-таблица называется нормальной, если все её строки лексографически положительны
Утв.Прямую с.-т. всегда можно преобразовать в нормальную с.-т. путем переобозначения переменных и изменения порядка расположения столбцов
Лексикографический вариант прямого симплекс-метода алгоритма:
0.построить нормальную симплекс-таблицу
1.если с.-т. является двойственно допустимой (т.е. ,j=1..n), то решение оптимальное и конец, иначе переход к шагу2
2.определяем ведущий столбец, т.е. находим такое j=s, что(если их несколько, то выбираем любой из них)
3. если , то конец (ЗЛП решения не имеет), иначе определяем ведущую строкуr:(если 2 одинаковых, то любой)
4.преобразуем симплекс-таблицу с ведущим элементом .(Заменяем соответствующую базисную переменную на небазисную) и переходим к шагу1 (в результате с.-т. остается всегда прямо допустимой)
Утв.Если ЗЛП вырождена, то алгоритм будет конечным (всегда)
Геометрическая интерпретация симплекс-метода.
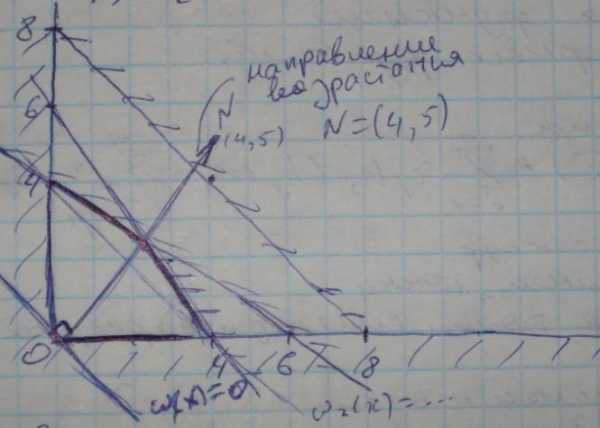
Решение лежит на границе области
25
studfiles.net