Оптимизация полимодальных одномерных целевых функций. Метод ломаных методы оптимизации
7 Метод ломаных
В формулах (5) величина n число шагов, задается перед началом вычислений. При k = n процесс вычислений заканчивается.
Теорема 3. Для задачи А метод n является единственным оптимальным последовательным методом на классе Q унимодальных функций. Наилучшая гарантированная точность множества последовательных методов Pn на классе Q равна
= b a.
Fn+2
Следствие. Кол-вонеобходимых при решении задачи А вычислений значенийф-иf(x) 2 Q гарантирующих погрешность6 " равно числу n, удовлетворяющему неравенствам
Предназначен для решения задач минимизации 1-огои2-оготипа для функций не являющихся унимодальными. Рассмотрим данный метод для класса функций, удовлетворяющих условию Липшица на отрезке и запишем определение. Говорят, чтоф-яудовлетворяет условию Липшица на отрезке [a; b], если существует постоянная L > 0 такая, что
jf(x) f(v)j 6 L jx vj 8x; v 2 [a; b] (1)
Постоянную L называют константой Липшица. Геометрический смысл условия (1) следующий: угловой коэффициент
jf(x) f(v)j 6 L jx vj
для всех точек из [a; b]
7.1Описание метода ломаных
Пусть ф-яf(x) удовлетворяет условию 1 на отрезке [a; b]. Зафиксируемкакую-либоточку v 2 [a; b] и определимф-ю
g(x; v) = f(v) L jx vj
переменной x, причем a 6 x 6 b. g(x; v) кусочно-линейнана [a; b], график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющие угловые коэффициенты L и пересекающихся в точке (v; f(v)). Кроме того в силу условия (1) выполняется неравенство:
f(x) g(x; v) > (L jf(x) f(v)j) jx vj > 0 (2)
jx vj
Покажем истинность левой части неравенства (2):
f(x) g(x; v) = f(x) f(v) + L jx vj
Запишем левую часть (2) в виде
f(x) f(v) + Ljx vj > (L jf(x) f(v)j)jx vj
jx vj
Отсюда следует, что
f(x) f(v) > jf(x) f(v)jjx vj
jx vj
т.е.
f(x) f(v) > jf(x) f(v)j
что выполняется всегда. Истинность левой части неравенства (2) доказана. Тогда из неравенства (2) следует, что
g(x; v) = f(v) Ljx vj 6 f(x) (3)
при всех x 2 [a; b]. Причем
studfiles.net
Оптимизация полимодальных одномерных целевых функций.
от требуемой абсолютной погрешности решения ε как первое число Фибоначчи, большее (В−А)/ε , т.e.
Nn>(B−A)/ε.
Координаты первых двух поисковых точек x1, x2 делят отрезок [B−A] на
участки, пропорциональные Nn-2 | и Nn-1,т.е. x1=A+ | Nn−2 | (B − A) ,x2=A+ | Nn−1 | (B + A). |
| |||||
|
| ||||
|
| Nn | Nn | ||
Если измеренное или вычисленное значение целевой функции F(x1) < F(x2) при необходимости отысканияэкстремума-минимума,то смещается правая граница первоначального интервала неопределенности, т.е. B = x2. Если F(x) >F(x2) , то смещается левая граница, т.е. принимается A = x1. Тогда длина нового интерва-
ла неопределенности становится пропорциональной Nn-1 ,то есть равной | Fn−1 |
| |||
F | |||||
|
|
| |||
|
|
| n | ||
части первоначального интервала неопределенности. После | к-oйитерации | ||||
длина к -гоинтервала неопределенности становится равной | Nn−k | части пер- | |||
| |||||
| Nn |
|
| ||
воначального интервала неопределенности, а поисковые точки в нем ,будут
иметь координаты x1(k) =A + | Nn−k −2 (B− A) | , x2 | (k) = | A + | Nn−k −1 (B− A) | Число итераций |
| Nn−k |
|
| Nn−k | ||
m необходимых для получения решения с заданной абсолютной погрешности ε известно заранее и равно n-2,так как N1=N2=1.
При каждой итерации в качестве одной из поисковых точек всегда оказывается одна из поисковых точек предыдущей итерации, значение целевой функции для которой уже вычислено или измерено. Следовательно, поиск Фибоначчи вдвое сокращает число поисковых экспериментов или вычислений целевой функции.
Метод ломаных
Метод ломаных разработан для оптимизации одномерных полимодальных функций. Функция J(U) называется липшицируемой на [a, b], если существует такое число L (константа Липшица), что для любых x, y из [a, b] верно неравенство |f(x)-f(y)|≤L·|x-y|.Т.е. постоянная Липшица - положительное число, равное или большее модуля максимального значения производной J’(U) на [a, b].
Необходимо найти значение управляемого параметра U, доставляющее глобальный экстремум-минимумнелинейной целевой функции с заданной абсолютной погрешностью при заданных ограничениях на управляемый параметр A≤U≤B. Выбирается произвольно начальная поисковая точка U0 [A,B] и составляется ломаная функция
g (U,U0)=J(U0)−L(U-U0).
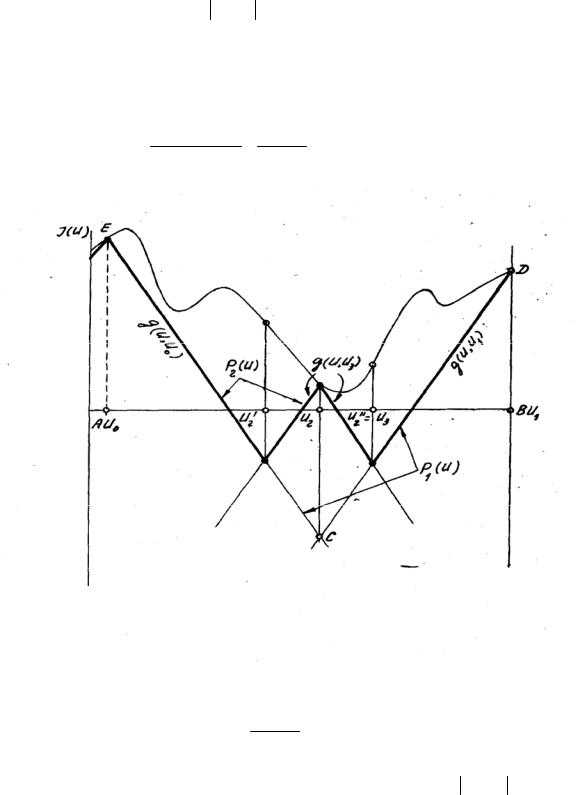
Очевидно, функция g(U,U0) состоит из двух отрезков и расположена ниже J(U), только в точке U = U0, т.е. g(U0) = J(U0). Затем вводится ломанная огибающая по максимуму Р0(U1) = g(U,U0). Следующая поисковая точка U1 определяется условием P0 (U1)= min P0(U). Для точки U1 опять рассматривается ломаная g(U,U1)=J(U1) − LU −U1 , и вводится огибающая по максимуму
P1(U) = max {P0(U), g(U,U1)} (ломаная FЕСВ на рис.). Следующая поисковая точка U2 определяется опять по условию P1(U2) = min P1(U) Однако, это будет точка пересечения P0(U) = g(U,U0) и g(U,U1). Значение U2, следовательно, определяется из уравнения g(U,U0)= g(U,U1) и равно
U2 = J(U0 ) − J(U1 ) +U0 +U1 ,
2L 2
Рисунок 1 Метод ломаных
Если J(U0) > J(U1), тоU2 > U0 2+U1 , то есть следующая поисковая точка сме-
щается относительно середины отрезка в сторону минимума J(U). Затем вводятся ломаная функция для точки U2 g(U1,U2) = J(U2) −LU −U2 и огибающая по
максимуму P2(U) = max {P1(U), g(U,U2)}. Следующая поисковая точка определяется по условию P2(U3) = min P2(U). Однако в данном случае точек минимума будет две - это точки пересечения g(U,U2) с P1(U)
studfiles.net
33. Метод золотого сечения решения задачи одномерной минимизации.
МЗС позволяет решить задачу с требуемой точностью при меньшем кол-ве вычислений значения функции.
Опр. Золотым сечением отрезка наз деление отрезка на 2 неравные части так, что отношение длины меньшей части к длине большей равно отношению длины большей части к длине всего отрезка.
Т-ки, кот. делят отрезок в золотом отношении
Описание МЗС. Решаем задачу . Положим а1=а,b1=b и найдем точки х1 и х2, котор делят [a1;b1] в золотом сечении. Вычислим и. Если, то положим а2=а1,b2=x2, . Если, то а2=х1,b2=b1, . Длина построенного отрезка [a2;b2] равна и точка, кот. делит отрезок [a2;b2] в золотом отношении.
Пусть на некотор. этапе найден отр-к , найдены т-ки х1, ,…,и вычислены значения,f(),…,f(). Длина отрезка . И на отрезкеесть т-ка, кот. делит этот отрезок в ЗО и в кот. вычислено значение целевой функции.
Определим следующ. т-ку по правилу .
Предположим, что (). Вычислим знач. ф-ции в т-ке.Если выполняется неравенство, полагаем. Если, то, в результате получим отрезок, имеющий непустое пересечение с мн-вом решений задачи, длина кот.
Если количество вычислений значений целевой ф-ции ничем не огранич., то процесс вычислений продолжается до тех пор, пока не будет выполнятся неравенство
Если количество вычислений значений целевой ф-ции ничем огранич., то процесс вычислений заканчивается, когда будет выполнено заданное число итераций. В качестве точки минимума выбираем т-ку с вычисленным в ней значением целевой ф-ции.
Погрешность этого метода:
Замечание. Преимуществом МЗС явл. тот факт, что на каждой итерации знач. ф-ции вычисляется только один раз.
Замечание. МЗС можно применять для нахождения минимума функции не являющейся унимодальной. Но в этом случае решение может находиться далеко от глобального минимума.
34. Обоснование метода ломаных решения задачи одномерной минимизации.
Метод ломаных применяется для решения задачи (1), без требования унимодальности ф-ции f, но эти ф-ии должны уд. усл. Липшица.
Опр. Говорят, что ф-ция уд.усл. Липшица на [a;b], если , что. (2) Геометрическое усл.Липшица означает, что угловой коэф-тхорд, кот соединяют две произвольные точки графика ф-цийy=f(x) не превосходит константы L.
Если ф-я уд.усл. Липшица на [a;b] то она явл-ся непрерывной на [a;b].
Т1: Пусть f(x)-определена и непрерывна на [a;b] и на каждом [ai;ai+1], где а=a1<a2<…<an<an+1=b уд. усл. Липшица с конст Li, тогда f(x)уд. усл Лип на всем отр-ке [a;b]с конст L=maxLi.
Д-во: выберем произвольные x,y из отрезка [a,b]. Предположим, что т-ка .
Рассм.модуль разности
Т2: Пусть f(x)–дифер на [a;b] и её производная огр-на на [a;b], тогда эта ф-ция уд. усл. Лип с конст. L=sup|f’(x)|
Д-во: т.к. ф-ция f(x) диф-ма, то по формуле конечных приращений приращение ф-ции
Отсюда и из ограниченности производной следует утв. теоремы.
Пусть ф-я f(x) удовлетворяет на [a;b] условию Липш (2) с константой L. Зафиксируем некоторую точку y из [a;b] и построим ф-цию
,
,
g(y,y)=f(y)
. Ф-ция g явл. кусочно-линейной ф-цией, ее график есть ломаная с углами наклона L (до y) и –L (после y) и в т-ке y g(y,y)=f(y).
Рассмотрим нерав-вот.е.,.
studfiles.net
Метод ломаных
Изобретательство Метод ломаных
просмотров - 323
Рассмотренные ранее методы одномерной оптимизации существенно используют свойство унимодальности минимизируемой функции . В случае если же функция этим свойством не обладает, ᴛ.ᴇ. является полимодальной, то погрешности в определении минимального значения и точек минимума функции бывают значительными.
Вместе с тем, применение этих методов приведет, вообще говоря, лишь в окрестность точки локального минимума, в которой значение функции может сильно отличаться от искомого минимального значения на отрезке. По этой причине представляется важным разработка методов поиска глобального минимума, позволяющих строить минимизирующие последовательности для функций, не обязательно являющихся унимодальными.
Для построения метода ломанных используются свойства липшицевых функций (см. определение 2.8 и свойства 1-5 там же).
Этот метод начинается с выбора произвольной точки в качестве начальной и составления вспомогательной функции , определенной на всем отрезке . Очевидно, что функция кусочно-линейна на и что график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющих угловые коэффициенты и , и пересекающихся в точке . Вместе с тем, при всех выполняется неравенство причем . Это значит, что график функции лежит выше ломаной при всех и имеет с ней общую точку .
Следующая точка определяется из условия . В силу линейности функции очевидно или . Далее берется новая вспомогательная функция и строится аппроксимирующая функция . Очередная точка находится из условия . Далее строятся новые функции и и точка такая, что . Итак далее (см. рис. 3.4)
Пуст точки , уже известны. Тогда составляется следующая функция и следующая точка определяется из условия
. (3.9)
В случае если минимум на достигается в нескольких точках, то в качестве можно взять любую из них. Метод ломаных описан.
Очевидно, что есть кусочно-линейная функция, график которой представляет собой непрерывную линию, состоящую из отрезков прямых с угловыми коэффициентами +L и –L.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, на каждом шаге метода ломанных задача минимизации функции заменяется более простой задачей минимизации кусочно-линейной функции , которая приближает функцию снизу, причем монотонно возрастают.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, с помощью метода ломаных можно получить решение задачи одномерной оптимизации (2.1) для функций удовлетворяющих условию Липшица. Этот метод не требует унимодальности функции, и более того, функция может иметь сколько угодно точек локального минимума на рассматриваемом отрезке. На каждом шаге метода ломаных нужно минимизировать кусочно-линейную функцию , что может быть сделано простым перебором известных вершин ломаной . При этом перебор существенно упрощается благодаря тому, что ломаная отличается от ломаной не более чем двумя новыми вершинами. К достоинствам метода относится и то, что он сходится при любом выборе начальной точки .
Отметим, что метод ломаных не возможно реализовать без знания константы Липшица . При определении константы Липшица можно непосредственно использовать определение 2.8 и замечания 1-5, приведенные вслед за этим определением. На практике, часто для оценки минимальной константы вычисляют угловые коэффициенты некоторого числа хорд, соединяющих точки графика минимизируемой функции. Максимальный из модулей этих коэффициентов является приближением снизу к , причем тем лучшим, чем меньше эти хорды.
Следует иметь в виду, что использование завышенной оценки для ухудшает сходимость метода ломаных, приводит к излишне большому количеству вычислений значений минимизируемой функции. В случае если же пользоваться заниженной оценкой для , то метод может привести к неправильному определению приближения минимального значения.
Контрольные вопросы
1. Какие методы называют прямыми методами минимизации?
2. Поясните достоинства и недостатки прямых методов минимизации.
3. Перечислить основные методы одномерного поиска.
4. Опишите метод равномерного поиска.
5. Как оценивается погрешность определения точки минимума функции методом равномерного поиска?
6. Какие возможности улучшения метода перебора реализованы в методе поразрядного поиска?
7. Приведите описание алгоритма метода поразрядного поиска.
8. Каков принцип построения методов исключения отрезков.
9. Чем выгодно отличаются методы исключения отрезков от методов перебора?
10. Опишите алгоритм метода деления отрезка пополам.
11. Как оценить число итераций метода дихотомии, крайне важное для определения точки минимума с заданной точностью?
12. Какими особенностями обладает метод золотого сечения?
13. Какими достоинствами обладает метод ломаных в сравнении с другими методами одномерного поиска?
Читайте также
Рассмотренные ранее методы одномерной оптимизации существенно используют свойство унимодальности минимизируемой функции . Если же функция этим свойством не обладает, т.е. является полимодальной, то погрешности в определении минимального значения и точек минимума... [читать подробенее]
oplib.ru
8 Метод ломаных Эйлера
страница 18.1. Метод ломаных Эйлера
В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.Идея метода заключается в том, что на малом промежутке изменения независимой переменной
интегральная кривая дифференциального уравнения
заменяется отрезком прямой (касательной) (8)
Отсюда и процесс можно повторить для промежутка и т.д.
Таким образом, интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера (рис.).
Рассмотрим задачу (1), где — непрерывно дифференцируемая функция в прямоугольнике , .Построим систему равноотстоящих узлов x, x, … ,x,
где x= x+ kh, k = 0,1,2, … , h — достаточно малый шаг интегрирования.Проведем касательную в точке к графику решения y = y(x) дифференциального уравнения (1) с угло-вым коэффициентом .
Уравнение этой касательной имеет вид: .
За приближенное решение уравнения в точке возьмем ординату точки пересечения касательной с прямой , т. е.
или .
Через точку проведем прямую с угловым коэффициентом , где определен только что выше: .Находим точку пересечения полученной прямой с прямой ,
ордината этой точки: , или .Продолжая этот процесс, получаем семейство отрезков прямых:
,
, (9)
где ,
Эти отрезки образуют ломаную, называемую ломаной Эйлера. Она является приближенным решением исходной задачи (1) методом ломаных Эйлера.
Метод Эйлера обладает удовлетворительной точностью лишь при достаточно малых . Действительно, разложим точное решение уравнения (1) в ряд Тейлора в окрестности узла :
.
Сравнив полученное выражение с формулой (9), приходим к выводу, что погрешность приближенного метода Эйлера .
Отметим, что особенностью метода Эйлера является то, что на каждом шаге интегрирования приближенное значение определяется через . Таким образом, на каждом отрезке решается задача Коши:
что удобно с точки зрения вычислений.
Метод Эйлера является
простейшим численным методом интегрирования дифференциального уравнения.Его недостатки:
- малая точность;
- систематическое накопление ошибок: погрешность каждого нового шага систематически возрастает.
Существуют различные уточнения метода Эйлера, повышающие его точность
8.2. Модификации метода Эйлера
Более точным является усовершенствованный метод Эйлера, при котором сначала вычисляют промежуточные значения:,
а затем полагают . (10)
Получим оценку точности построенного метода. Для этого разложим точное решение (1) в ряд Тейлора в окрестности точки , получим:
,
,
отсюда
или ,
а это значит .
Сравнив полученную формулу с (10), получим погрешность . Другой модификацией метода Эйлера является усовершенствованный метод Эйлера — Коши, при котором сначала определяется «грубое» приближение решения: .
Исходя из данного выражения, вычисляют: .
Затем приближенно полагают . (11) Усовершенствованный метод Эйлера — Коши можно еще более уточнить, применяя итерационную обработку каждого значения . А именно, исходя из грубого приближения ,
строится итерационный процесс , (12)
Итерирации продолжаются до тех пор, пока некоторые два последовательных приближения и станут меньше заданной погрешности.
После этого принимается ,
где — общая часть приближений и .
Отметим, что метод Эйлера с итерационной обработкой дает на каждом шаге погрешность порядка и нередко применяется в вычислительной практике.
8.3. Метод Рунге — Кутта
Этот метод является одним из методов повышенной точности и относится к одношаговым методам численного интегрирования задачи Коши (1), т. е. к таким методам, которые позволяют найти приближенное значение решения заданной задачи в узле по информации об этом решении лишь в одной предыдущей узловой точке .Метод Рунге — Кутта является одним из самых распространенных методов решения задач с начальными условиями для обыкновенных дифференциальных уравнений.
Метод описывается следующими шестью соотношениями:
, ,
, ,
, .
Как видно, с алгоритмической точки зрения метод Рунге — Кутта не имеет принципиальных различий от метода Эйлера. Разница лишь в объеме вычислений: для получения нового значения на каждом шаге необходимо проделать все действия, предусмотренные формулами выше.
Метод Рунге — Кутта является методом повышенной точности (он имеет четвертый порядок точности), несмотря на свою трудоемкость широко используется при численном решении уравнений с помощью компьютера.
На практике применяется следующий способ контроля точности — двойной счет. Если — вычисленное значение с шагом , а — соответствующее узловое значение, полученное с шагом , то для ориентировочной оценки погрешности последнего значения можно использовать формулу:
.
страница 1gymnazya.ru
Метод ломаных
Рассмотренные ранее методы одномерной оптимизации существенно используют свойство унимодальности минимизируемой функции . Если же функция этим свойством не обладает, т.е. является полимодальной , то погрешности в определении минимального значения и точек минимума функции могут быть значительными.
Кроме того, применение этих методов приведет, вообще говоря, лишь в окрестность точки локального минимума, в которой значение функции может сильно отличаться от искомого минимального значения на отрезке. Поэтому представляется важным разработка методов поиска глобального минимума, позволяющих строить минимизирующие последовательности для функций, не обязательно являющихся унимодальными.
Одним из таких методов минимизации полимодальных функций является метод ломаных . Однако данный метод так же имеет ограничение, он применим для минимизации функций, удовлетворяющих условию Липшица на отрезке.
Для построения метода ломанных используются свойства липшицевых функций (см. определение 2.8 и свойства 1-5 там же).
Этот метод начинается с выбора произвольной точки в качестве начальной и составления вспомогательной функции , определенной на всем отрезке . Очевидно, что функция кусочно-линейна на и что график ее представляет собой ломаную линию, составленную из отрезков двух прямых, имеющих угловые коэффициенты и , и пересекающихся в точке . Кроме того, при всех выполняется неравенство причем . Это значит, что график функции лежит выше ломаной при всех и имеет с ней общую точку .
Следующая точка определяется из условия . В силу линейности функции очевидно или . Далее берется новая вспомогательная функция и строится аппроксимирующая функция . Очередная точка находится из условия . Далее строятся новые функции и и точка такая, что . Итак далее (см. рис. 3.4)
Пуст точки , уже известны. Тогда составляется следующая функция и следующая точка определяется из условия
. (3.9)
Если минимум на достигается в нескольких точках, то в качестве можно взять любую из них. Метод ломаных описан.
Очевидно, что есть кусочно-линейная функция, график которой представляет собой непрерывную линию, состоящую из отрезков прямых с угловыми коэффициентами +L и –L.
Таким образом, на каждом шаге метода ломанных задача минимизации функции заменяется более простой задачей минимизации кусочно-линейной функции , которая приближает функцию снизу, причем монотонно возрастают.
Таким образом, с помощью метода ломаных можно получить решение задачи одномерной оптимизации (2.1) для функций удовлетворяющих условию Липшица. Этот метод не требует унимодальности функции, и более того, функция может иметь сколько угодно точек локального минимума на рассматриваемом отрезке. На каждом шаге метода ломаных нужно минимизировать кусочно-линейную функцию , что может быть сделано простым перебором известных вершин ломаной . При этом перебор существенно упрощается благодаря тому, что ломаная отличается от ломаной не более чем двумя новыми вершинами. К достоинствам метода относится и то, что он сходится при любом выборе начальной точки .
Отметим, что метод ломаных не возможно реализовать без знания константы Липшица . При определении константы Липшица можно непосредственно использовать определение 2.8 и замечания 1-5, приведенные вслед за этим определением. На практике, часто для оценки минимальной константы вычисляют угловые коэффициенты некоторого числа хорд, соединяющих точки графика минимизируемой функции. Максимальный из модулей этих коэффициентов является приближением снизу к , причем тем лучшим, чем меньше эти хорды.
Следует иметь в виду, что использование завышенной оценки для ухудшает сходимость метода ломаных, приводит к излишне большому количеству вычислений значений минимизируемой функции. Если же пользоваться заниженной оценкой для , то метод может привести к неправильному определению приближения минимального значения.
Контрольные вопросы
1. Какие методы называют прямыми методами минимизации?
2. Поясните достоинства и недостатки прямых методов минимизации.
3. Перечислить основные методы одномерного поиска.
4. Опишите метод равномерного поиска.
5. Как оценивается погрешность определения точки минимума функции методом равномерного поиска?
6. Какие возможности улучшения метода перебора реализованы в методе поразрядного поиска?
7. Приведите описание алгоритма метода поразрядного поиска.
8. Каков принцип построения методов исключения отрезков.
9. Чем выгодно отличаются методы исключения отрезков от методов перебора?
10. Опишите алгоритм метода деления отрезка пополам.
11. Как оценить число итераций метода дихотомии, необходимое для определения точки минимума с заданной точностью?
12. Какими особенностями обладает метод золотого сечения?
13. Какими достоинствами обладает метод ломаных в сравнении с другими методами одномерного поиска?
studlib.info
Методы оптимизации|ИТММ ННГУ
Кафедра информатики и автоматизации научных исследований
Специальность: Прикладная информатика
Преподаватель: Коротченко А.Г.
Целями освоения дисциплины (модуля) «Методы оптимизации» являются ознакомление студентов с вопросами построения оптимизационных математических моделей для конкретных предметных областей, обучение студентов основным понятиям теории нелинейной оптимизации и методам решения экстремальных задач. В курсе изучаются условия оптимальности в задачах математического программирования, элементы выпуклого анализа и теории оптимального управления, методы решения задач безусловной и условной оптимизации.
В курс включены основные понятия, изучаемые в таких дисциплинах как математический анализ, алгебра и геометрия дифференциальные уравнения, математические основы информатики. К дисциплинам, для которых освоение данной дисциплины необходимо как предшествующее, относится дисциплина базовой части математического и естественнонаучного цикла «Теория систем и системный анализ».
В результате освоения дисциплины обучающийся должен:
Знать: условия оптимальности в задачах безусловной оптимизации, классической задаче на условный экстремум, задачах выпуклой оптимизации, задачах математического программирования, основные понятия о простейших задачах вариационного исчисления и оптимального управления.
Уметь: применять условия оптимальности для анализа экстремальных задач из различных классов, доказывать основные теоремы теории нелинейной оптимизации.
Владеть: представлениями (навыками) в решении нелинейных задач оптимизации (методы нулевого порядка, сопряженных градиентов, условного градиента, методы штрафов, методы решения многоэкстремальных задач).
Содержание
1. НЕЛИНЕЙНЫЕ ОПТИМИЗАЦИОННЫЕ МОДЕЛИ. ЗАДАЧА БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ И КЛАССИЧЕСКАЯ ЗАДАЧА НА УСЛОВНЫЙ ЭКСТРЕМУМ. Понятие о задачах оптимизации. Примеры оптимизационных задач. Схема вычислительного эксперимента. Теоремы существования решения задач поиска экстремума. Необходимые и достаточные условия оптимальности в задаче безусловной оптимизации. Классическая задача на условный экстремум. Функция Лагранжа. Теоремы о необходимом условии оптимальности первого и второго порядка. Достаточные условия оптимальности.
2.ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА. УСЛОВИЯ ОПТИМАЛЬНОСТИ В ЗАДАЧАХ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ. ЭЛЕМЕНТЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ. Выпуклые множества и выпуклые функции. Примеры. Внутренние операции в классе выпуклых функций. Выпуклая задача оптимизации и ее основные свойства. Дифференциальные критерии выпуклости. Сильно выпуклые функции и критерии сильной выпуклости. Теорема существования и единственности решения выпуклой задачи с сильно выпуклой целевой функцией. Проекция точки на множество. Теорема о разделяющей гиперплоскости и теорема об опорной гиперплоскости. Теорема отделимости. Теорема Фана. Необходимые условия оптимальности в терминах направлений. Дифференциальное условие оптимальности в задаче минимизации функции на выпуклом множестве. Конкретизация дифференциального условия оптимальности в задаче минимизации функции на выпуклом множестве для случаев, когда допустимое множество является гиперпараллелепипедом и неотрицательным октантом. Задача математического программирования. Необходимые условия оптимальности в задаче математического программирования (принцип Лагранжа). Условия регулярности в задаче математического программирования. Достаточные условия оптимальности, определяемые принципом Лагранжа, для регулярной задачи выпуклого программирования. Теорема Куна-Таккера. Достаточные условия оптимальности в общей задаче математического программирования. Вектор Куна-Таккера. Теорема существования вектора Куна-Таккера, Основные теоремы теории двойственности. Теорема Куна-Таккера в форме двойственности. Формулировка принципа максимума. Простейшая задача оптимального быстродействия. Задача вариационного исчисления.
3. ОПТИМАЛЬНЫЕ АЛГОРИТМЫ ПОИСКА ЭКСТРЕМУМА. МЕТОДЫ ОПТИМИЗАЦИИ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ. Унимодальные функции. Оптимальный пассивный метод поиска минимума унимодальных функций. Метод Фибоначчи. Метод золотого сечения. Оптимальный пассивный метод поиска минимума липшицевых функций. Точная нижняя миноранта для функций, удовлетворяющих условию Липшица. Свойства точной нижней миноранты. Метод ломаных. Метод кусочно-линейной аппроксимации.
4. КЛАССИЧЕСКИЕ ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ БЕЗУСЛОВНОЙ И УСЛОВНОЙ ОПТИМИЗАЦИИ. НЕКОТОРЫЕ МЕТОДЫ РЕШЕНИЯ МНОГОЭКСТРЕМАЛЬНЫХ ЗАДАЧ. Начальные сведения о численных методах оптимизации функций многих переменных. Сходимость и скорость сходимости методов оптимизации. Условия остановки. Направление убывания. Выбор длины шага в методах спуска. Градиентный метод. Сходимость в случае невыпуклой минимизируемой функции. Сходимость и оценка скорости сходимости в случае сильно выпуклой минимизируемой функции. Обсуждение метода. Примеры. Метод Ньютона и его модификации. Квазиньютоновские методы. Примеры. Понятие сопряженных направлений и их свойства. Методы сопряженных направлений. Метод сопряженных градиентов. Метод сопряженных направлений нулевого порядка. Метод Хука-Дживса. Метод Нелдера-Мида. Примеры. Метод проекции градиента. Теорема сходимости. Обсуждение метода. Метод условного градиента и его сходимость. Конечный метод решения задач квадратичного программирования. Метод линеаризации. Сходимость метода штрафных функций. Оценки скорости сходимости. Простейший алгоритм метода штрафов. Примеры. Метод параметризации целевой функции. Методы, основанные на редукции размерности. Методы, основанные на априорной информации о минимизируемой функции.
Лабораторный практикум
1.Построение нелинейных оптимизационных моделей. Задача безусловной оптимизации. Классическая задача на условный экстремум.
2. Выпуклые множества и выпуклые функции. Критерии выпуклости и сильной выпуклости. Выпуклая задача оптимизации. Теорема существования и единственности. Условие оптимальности в задаче минимизации функции на выпуклом множестве. Задача математического программирования. Принцип Лагранжа. Условия регулярности в задаче математического программирования. Теорема Куна - Таккера в дифференциальной форме.
3. Метод Фибоначчи. Метод золотого сечения. Оптимальный одношаговый метод в классах, определяемых априорной информацией о минимизируемой функции. Метод ломаных.
4. Градиентный метод. Квазиньютоновские методы. Методы сопряженных направлений. Метод проекции градиента. Метод условного градиента. Метод линеаризации. Методы штрафов.
Литература
а) основная литература
- Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 19801.
- Васильев Ф.П. Методы решения экстремальных задач. – М.: Наука, 1981
- Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986
- Карманов В.Г. Математическое программирование. – М.: Наука, 1986
б) дополнительная литература
- Хедли Дж. Нелинейное и динамическое программирование. – М.: Мир, 1967
- Зангвилл У.И. Нелинейное программирование. Единый подход. – М.: Советское радио, 1973
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф.
- Математическая теория оптимальных процессов. - М.: Наука, 1976
- Стронгин Р.Г. Численные методы в многоэкстремальных задачах. – М.: Наука, 1978
- 5.. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978
- Черноусько Ф.Л., Меликян А.А. Игровые задачи управления и поиска. – М.: Наука, 1978
- Немировский А.С., Юдин Д.Б. Сложность задач и эффективность методов оптимизации. М.: Наука, 1979
- Ашманов С.А. Линейное программирование. – М.: Наука, 1981
- 9.Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982
- Розен В.В. Цель- оптимальность- решение: математические модели принятия оптимальных решений. – М.: Радио и связь, 1982
- Батищев Д.И. Методы оптимального проектирования. – М.: Радио и связь, 1984
- Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. – М.: Высшая школа, 1986
- Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь, 1988
- Коротченко А.Г. Методические указания для самостоятельной работы студентов специальности «прикладная математика» при изучении темы «Методы поиска экстремума функций одной переменной» в курсе «Моделирование выбора решений». – Изд. ГГУ, Горький, 1990
- Батищев Д.И., Коган Д.И. Вычислительная сложность экстремальных задач переборного типа. – Изд. ННГУ, Н.Новгород, 1994
- Коротченко А.Г., Тихонов В.А. Методические указания (сборник задач) по курсу «Модели и методы принятия решений». – Изд. ННГУ, Н.Новгород, 2000
- Коротченко А.Г., Сморякова В.М., Кучина О.М., Малаховская Д.А. Методическая разработка по курсу «Системы принятия решений». – Фонд компьютерных изданий ННГУ, www.unn.ru/syst _ pr.doc,2010
- Коротченко А.Г., Сморякова В.М., Кучина О.М., Малаховская Д.А. Методическая разработка (сборник задач) по курсу «Системы принятия решений». – Фонд компьютерных изданий ННГУ, www.unn.ru/task_ pr.doc,2010
Отчетность
- Семестр 5: Зач
- Семестр 6: Экз
www.itmm.unn.ru