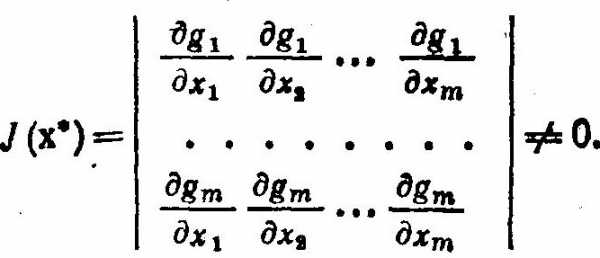2. Оптимальные системы управления. Метод лагранжа оптимизация
4.1. Множители лагранжа
Рассмотрим задачу условной оптимизации, содержащую только ограничения в виде равенств
min
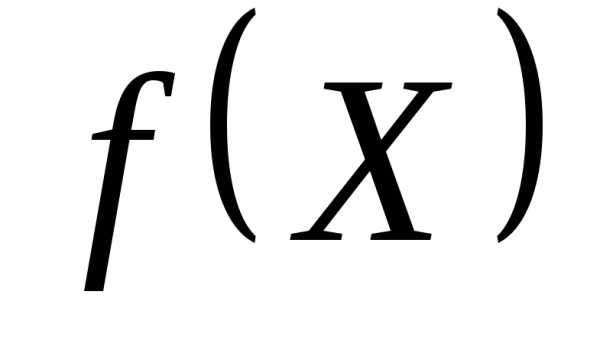
при наличии ограничений
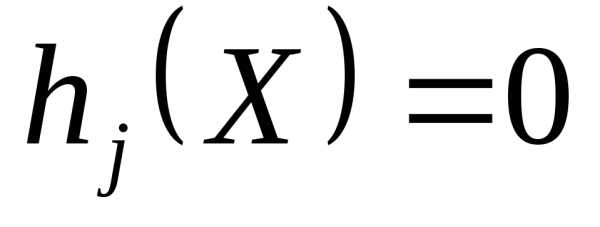 , .
, .
Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции m независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи. Новая задача может быть решена с помощью подходящего метода безусловной оптимизации.
Пример. Требуется минимизировать функцию
при ограничении
.
Исключив переменную 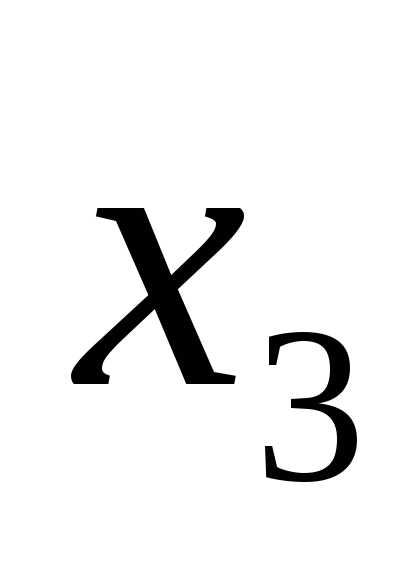
минимизировать ,
которую можно решить одним из методов безусловной оптимизации.
Однако метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого набора переменных. При наличии большого числа ограничений в виде равенств процесс исключения переменных становится весьма трудоемкой процедурой. Кроме того, возможны ситуации, когда уравнение не удается разрешить относительно переменной. В этом случае целесообразно использовать метод множителей Лагранжа.
С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде равенств.
Рассмотрим задачу
min
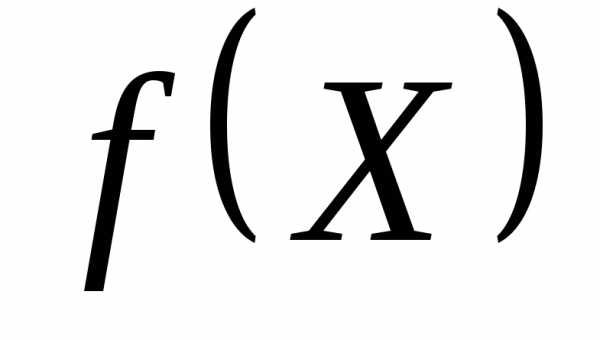
при наличии ограничений
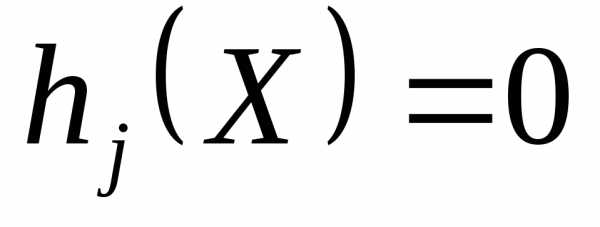
Из курса математического анализа хорошо известно, что точка условного минимума функции  совпадает с седловой точкой функции Лагранжа:
совпадает с седловой точкой функции Лагранжа:
,
при этом седловая точка должна обеспечивать минимум по переменным 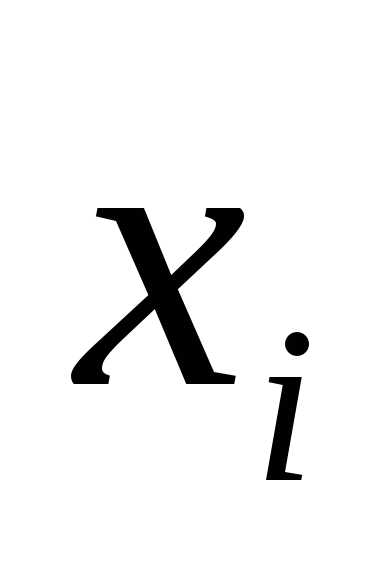 и максимум по параметрам
и максимум по параметрам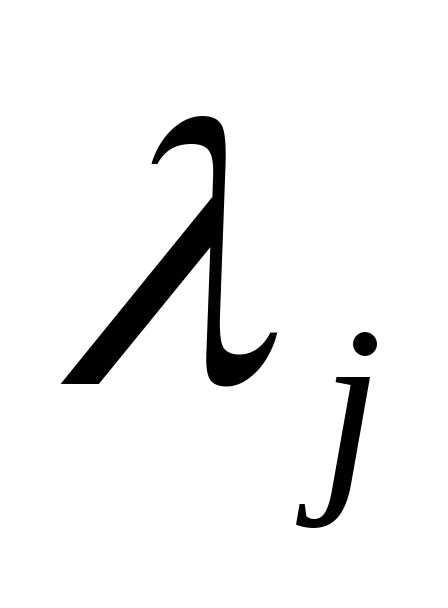 . Эти параметры называются множителями Лагранжа. Приравнивая частные производные функции
. Эти параметры называются множителями Лагранжа. Приравнивая частные производные функции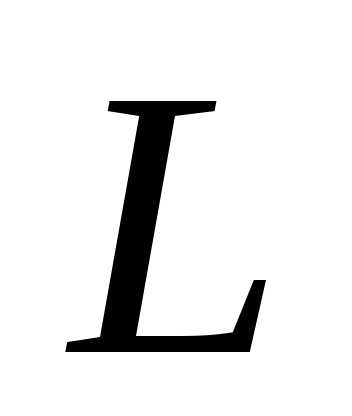 по
по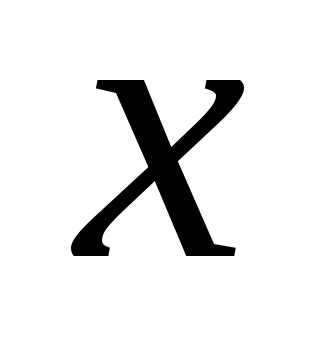 и по
и по к нулю, получим необходимые условия стационарной точки:
к нулю, получим необходимые условия стационарной точки:
, 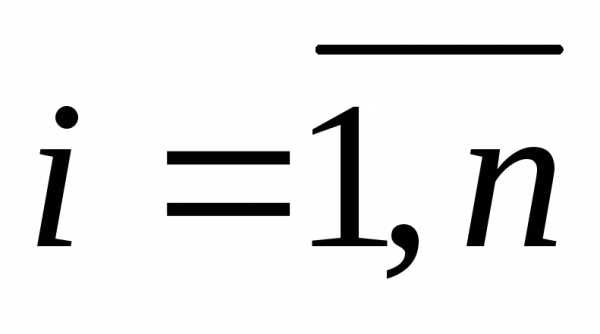 ,
,
, 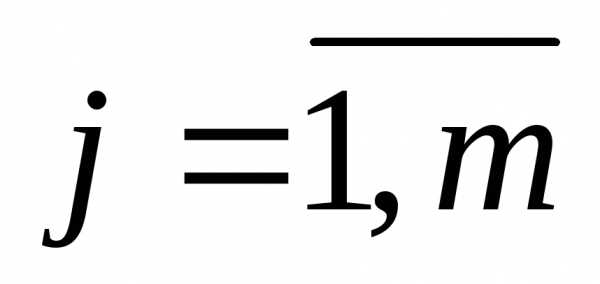 .
.
Решение системы 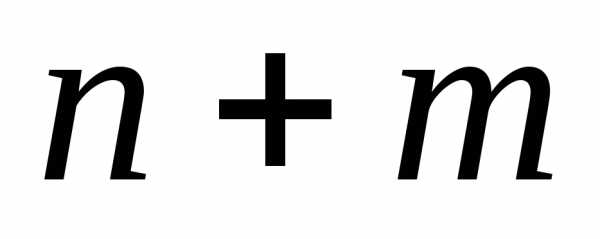 уравнений определяет стационарную точку функции Лагранжа. Достаточные условия существования минимума исходной задачи содержат, кроме выше упомянутых, положительную определенность матрицы Гессе целевой функции.
уравнений определяет стационарную точку функции Лагранжа. Достаточные условия существования минимума исходной задачи содержат, кроме выше упомянутых, положительную определенность матрицы Гессе целевой функции.
4.2. Условия куна - таккера
Рассмотрим задачу нелинейного программирования с ограничениями в виде неравенств
min
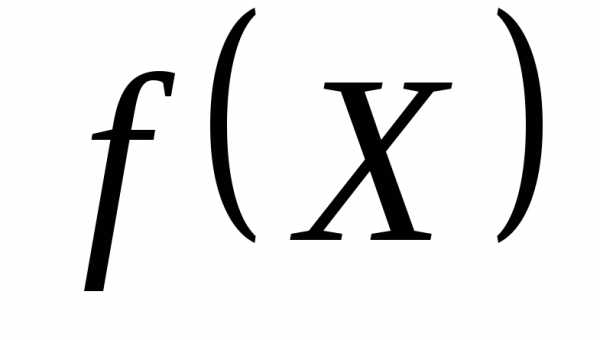
при ограничениях
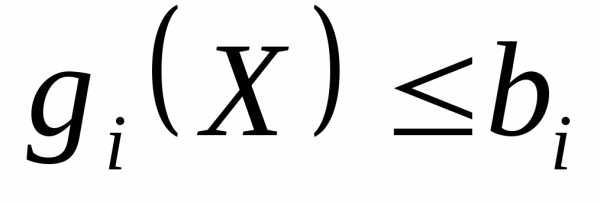 , .
, .
Сведем ограничения в виде неравенств к ограничениям-равенствам добавлением к каждому из них ослабляющих переменных 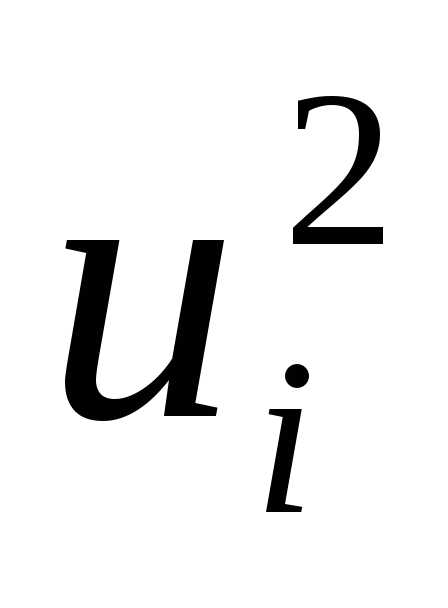 ,
,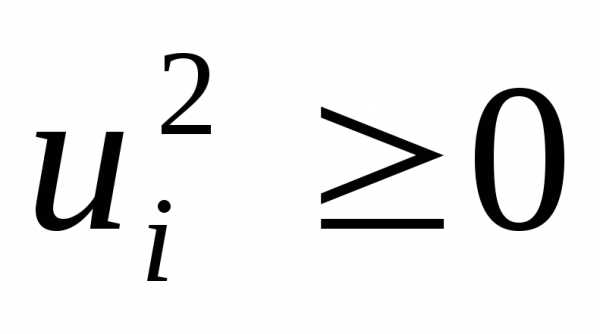 :
:

 .
.
Сформируем функцию Лагранжа:
.
Тогда необходимые условия минимума принимают вид
, 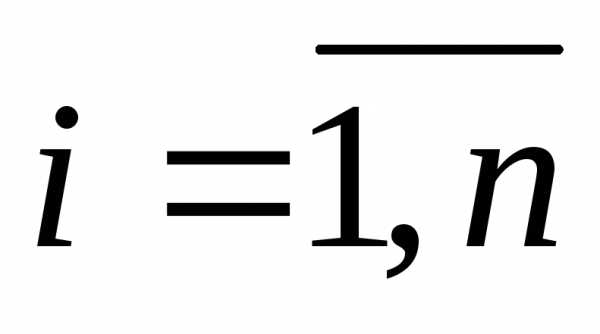 ;
;
, 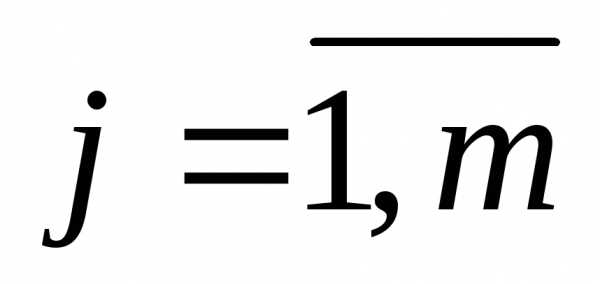 ;
;
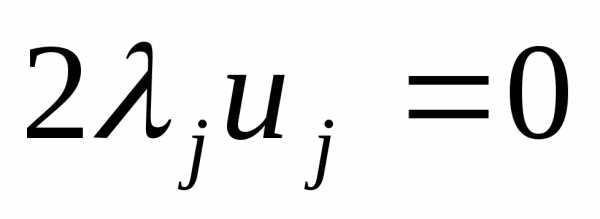 ,
, 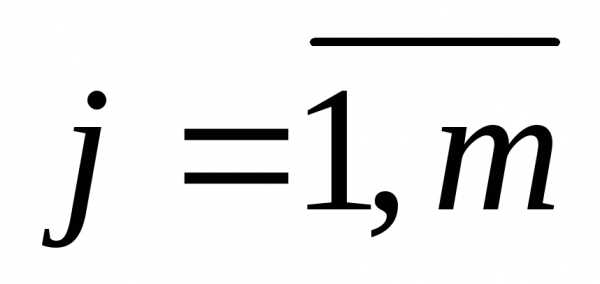
Можно умножить последнее уравнение на 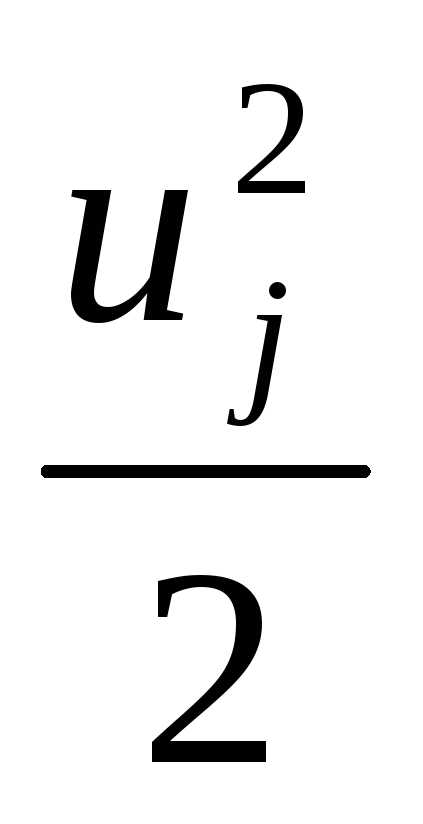 и заменить ослабляющие переменные, выразив их из второго уравнения. Второе уравнение можно преобразовать, отбросив ослабляющие переменные и переходя к ограничениям-неравенствам. Следует добавить еще одно условие
и заменить ослабляющие переменные, выразив их из второго уравнения. Второе уравнение можно преобразовать, отбросив ослабляющие переменные и переходя к ограничениям-неравенствам. Следует добавить еще одно условие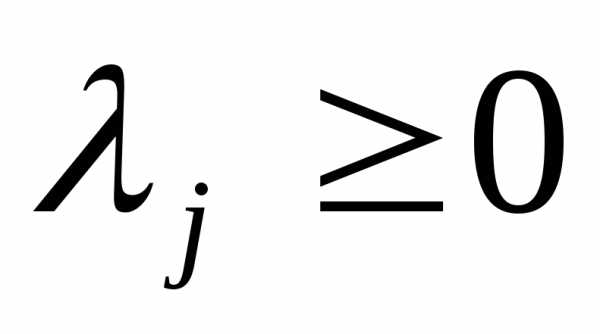 , которое должно выполняться в точке условного минимума.
, которое должно выполняться в точке условного минимума.
Окончательно получаем необходимые условия существования минимума задачи нелинейного программирования с ограничениями неравенствами, которые называются условиями Куна- Таккера:
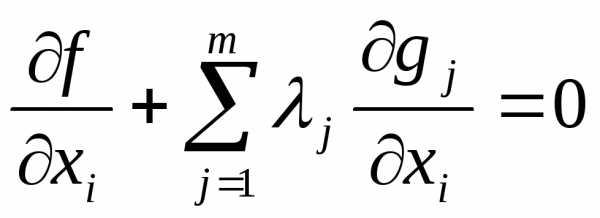 ,
,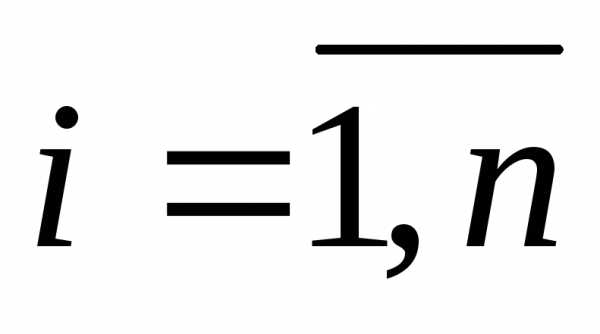 ; (1)
; (1)
,; (2)
,; (3)
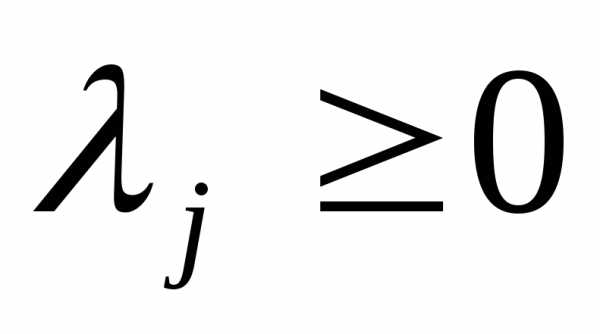 ,. (4)
,. (4)
Ограничение в виде неравенства 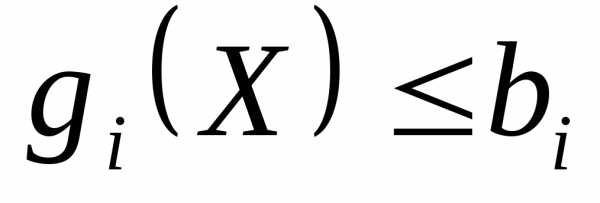 называется активным в точке
называется активным в точке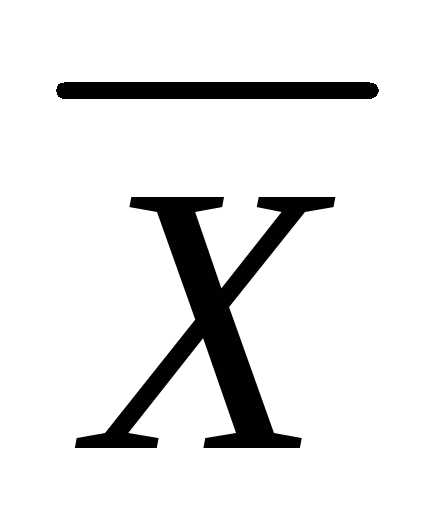 , если оно превращается в равенство
, если оно превращается в равенство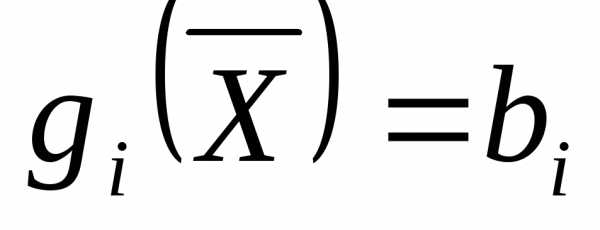 , и называется неактивным, если
, и называется неактивным, если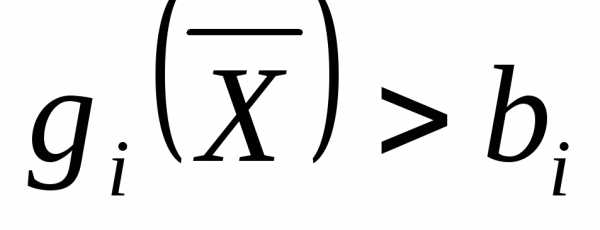
Уравнение (3) означает, что либо 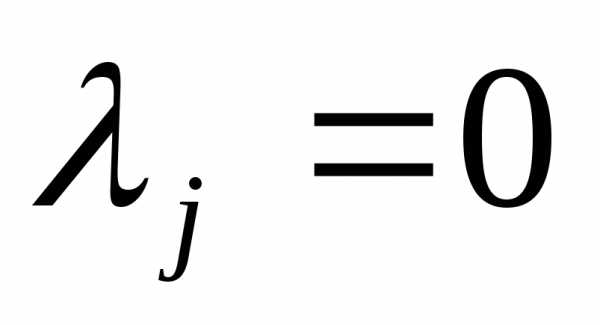 , либо. Если
, либо. Если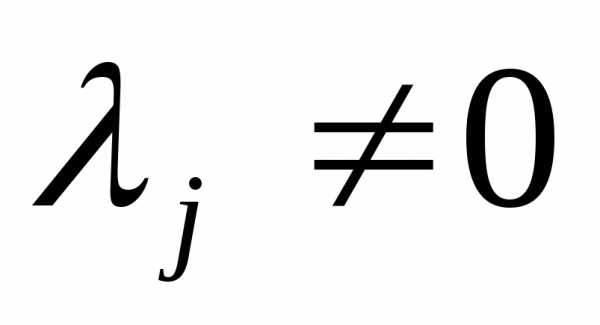 , тои ограничение является активным и представляет собой ограничение равенство. С другой стороны, если ограничение является строгим неравенством, то множитель Лагранжа будет иметь вид
, тои ограничение является активным и представляет собой ограничение равенство. С другой стороны, если ограничение является строгим неравенством, то множитель Лагранжа будет иметь вид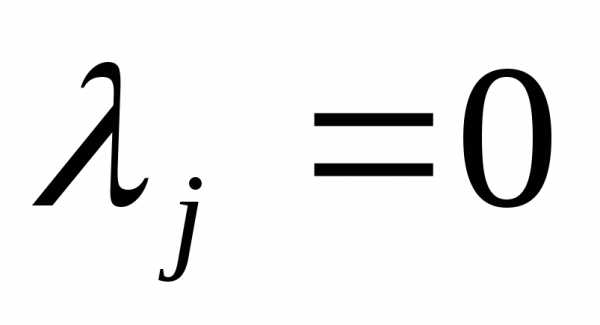 т.е. ограничениеявляется неактивным и им можно пренебречь. Конечно, предварительно не известно какими ограничениями можно пренебречь.
т.е. ограничениеявляется неактивным и им можно пренебречь. Конечно, предварительно не известно какими ограничениями можно пренебречь.
studfiles.net
2. Оптимальные системы управления
Оптимальное управление применяют как в технических системах для повышения эффективности производственных процессов, так и в системах организационного управления для совершенствования деятельности предприятий, организаций, фирм и отраслей народного хозяйства.
В организационных системах обычно интересуются конечным, установившимся результатом управления, не исследуя эффективность во время переходного процесса между подачей команды для управления и получением окончательного результата. Объясняется это тем, что в таких системах установившейся режим значительно более длителен, чем переходной процесс, и потери в переходном режиме несущественно влияют на величину выигрыша в установившемся режиме. Методы оптимизации конечных состояний сводятся к поиску минимума аналитических функции при различных ограничениях, которые мы рассматривали в предыдущих лабораторных занятиях.
В управлении динамическими техническими системами оптимизация существенна именно для переходных процессов, в которых показатель эффективности зависит не только от текущих значений координат, но и от характера изменения в прошлом, настоящем и будущем, и выражается некоторым функционалом от координат, их производных и времени. Проблемы управления в такой постановке решаются методами теории оптимальных систем управления.
Наиболее известны три метода решения задач оптимального управления: метод классического вариационного управления, принцип максимума Понтрягина, метод динамического программирования Беллмана.
2.1 Метод множителей Лагранжа
Два первых метода основаны на простейшей задаче вариационного исчисления: найти экстремум функционала
(3.1)
Функция, которая доставляет экстремум функционалу, должна удовлетворять уравнению Эйлера
(3.2)
В том случае, когда функция является функцией многих переменных f(y1,y2, …,yn,t), то вместо одного уравнения (3.2) получится система дифференциальных уравнений, которые имеют вид (3.2) для каждой из переменных.
Рассмотрим задачу оптимального управления:
(3.3)
( 3.4)
(3.5)
(3.6)
где уравнения (3.3) – уравнения объекта управления, (3.4) – ограничения на аргументы x и u функционала J, (3.5) – граничные условия, (3.6) – критерий оптимальности. Эта задача оптимального управления называется задачей Лагранжа с закрепленными концами и фиксированным временем.
Составляется функция Лагранжа
(3.7)
где i – функции времени, k , 0 – постоянные, которые называются множителями Лагранжа. Прием Лагранжа состоит в том, что задача (3.3) – (3.6) преобразуется в простейшую задачу вариационного исчисления для интегрального выражения
(3.8)
В преобразованной задаче роль независимого аргумента играет вектор y = (x, u, , ), а роль подынтегральной функции – функция Лагранжа. Тогда по аналогии с простейшей задачей вариационного исчисления, с учетом того, что в функцию Лагранжа не входит производные функций u, , , уравнения Эйлера-Лагранжа принимают вид
(3.9)
Уравнения Эйлера-Лагранжа записывают, также используя Гамильтона
(3.10)
Тогда функция Лагранжа имеет вид
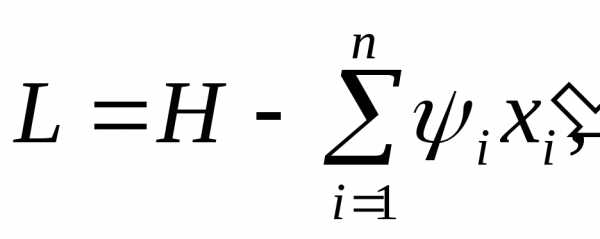 (3.10)
(3.10)
и из уравнений (3.9) с учетом функции Гамильтона получаем
(3.11)
(3.12)
Правило множителей Лагранжа: если допустимая пара (u(t), x(t)) является решением задачи оптимального управления (3.3) - (3.6), то найдутся такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера-Лагранжа (3.11).
Согласно этому правилу, чтобы найти оптимальное управление и оптимальную траекторию, надо решить совместно уравнения (3.3), (3.4), (3.11), (3.12) при краевых условиях (3.5). Для определения 2n+r+l неизвестных xi (i = 1,2, … , n), i (i = 1,2, …, n), uj (j = 1,2, …, r), k (k = 1,2, …, l) имеется столько же уравнений. Среди них имеются 2n дифференциальных уравнений (3.3) и (3.11), при решении которых можно использовать 2n краевых условия (3.5). Уравнения (3.4) и (3.12) являются функциональными. При решении практических задач вызывают трудности решение дифференциальных уравнений с краевыми условиями. В системе MATLAB можно получить аналитическое решение линейных стационарных дифференциальных уравнений. Это обстоятельство существенно облегчает задачу синтеза оптимальных алгоритмов управления линейных стационарных систем.
Множители Лагранжа входят в уравнения Эйлера-Лагранжа линейно и однородно. Поэтому они определяются с точностью до постоянного множителя. Поэтому один из множителей Лагранжа можно приравнять числу, отличному от нуля. Условились в неособом случае (0 0) принимать 0 = -1.
Применяя метод множителей Лагранжа, определяют управление как функции времени, т.е. проводится синтез алгоритма разомкнутого управления.
Во многих прикладных задачах на управление накладывается ограничение типа неравенства. Часто оптимальное управление в таких задачах имеет разрыв. Метод множителей Лагранжа не позволяет определить число и местоположение точек разрыва, и поэтому в этих случаях он не позволяет находить оптимальное управление. Такие задачи эффективно решаются с помощью максимума Понтрягина, сформулированный академиком Л.С. Понтрягиным в 1953 году.
studfiles.net
Династия Лекция 2 Повторение производных Оптимизация Метод Лагранжа
 Династия. Лекция 2 Повторение производных. Оптимизация. Метод Лагранжа. Введение понятия математического ожидания.
Династия. Лекция 2 Повторение производных. Оптимизация. Метод Лагранжа. Введение понятия математического ожидания.
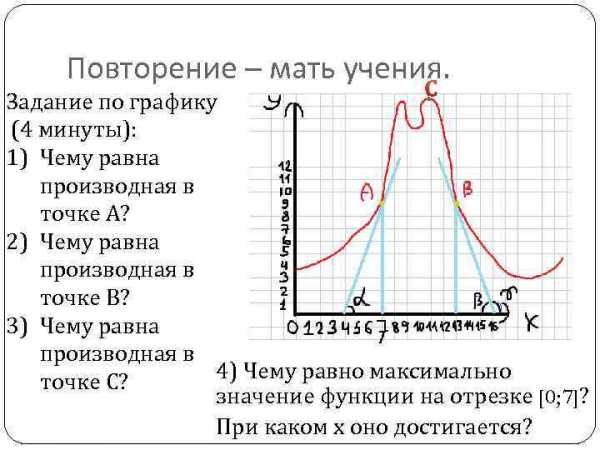 Повторение – мать учения. С Задание по графику (4 минуты): 1) Чему равна производная в точке А? 2) Чему равна производная в точке В? 3) Чему равна производная в 4) Чему равно максимально точке С? значение функции на отрезке [0; 7]? При каком х оно достигается?
Повторение – мать учения. С Задание по графику (4 минуты): 1) Чему равна производная в точке А? 2) Чему равна производная в точке В? 3) Чему равна производная в 4) Чему равно максимально точке С? значение функции на отрезке [0; 7]? При каком х оно достигается?
 Производные. Основные формулы
Производные. Основные формулы
 Производные. Основные формулы
Производные. Основные формулы
 Производная сложной функции Домашнее задание: доведите вычисления до конца
Производная сложной функции Домашнее задание: доведите вычисления до конца
 Оптимизация Процесс нахождения экстремума функции, т. е. выбор наилучшего варианта из множества возможных, процесс выработки оптимальных решений.
Оптимизация Процесс нахождения экстремума функции, т. е. выбор наилучшего варианта из множества возможных, процесс выработки оптимальных решений.
 Немного определений… Издержки TC — это оплата затрачиваемых ресурсов Доход (выручку) TR - денежные средства, полученные (вырученные) предприятием, фирмой, предпринимателем от продажи товаров и услуг Разность между доходом ТR и ее издержками TC равна прибыли PR, т. е. PR = TR - TC
Немного определений… Издержки TC — это оплата затрачиваемых ресурсов Доход (выручку) TR - денежные средства, полученные (вырученные) предприятием, фирмой, предпринимателем от продажи товаров и услуг Разность между доходом ТR и ее издержками TC равна прибыли PR, т. е. PR = TR - TC
 Оптимизируем? Однофакторная функция без ограничения Двухфакторная функция без ограничения Двухфакторная функция с ограничением => Лагранж
Оптимизируем? Однофакторная функция без ограничения Двухфакторная функция без ограничения Двухфакторная функция с ограничением => Лагранж
 Однофакторная функция без ограничения Пример Пусть издержки фирмы: Выручку можно найти по формуле: Тогда для прибыли фирмы имеем выражение: ИК
Однофакторная функция без ограничения Пример Пусть издержки фирмы: Выручку можно найти по формуле: Тогда для прибыли фирмы имеем выражение: ИК
 Пример Аналитическое решение задачи: используем условие первого порядка, т. е. найдем производную прибыли по переменной x и приравняем эту производную к нулю:
Пример Аналитическое решение задачи: используем условие первого порядка, т. е. найдем производную прибыли по переменной x и приравняем эту производную к нулю:
 Пример Что делать дальше? 1). Сравнить прибыли в точках 2). Использовать условие второго порядка, которое гласит, что если вторая производная прибыли по переменной x в точке x* отрицательна, то точка x* — точка максимума функции
Пример Что делать дальше? 1). Сравнить прибыли в точках 2). Использовать условие второго порядка, которое гласит, что если вторая производная прибыли по переменной x в точке x* отрицательна, то точка x* — точка максимума функции
 Пример Вывод: х=4
Пример Вывод: х=4
 Двухфакторная функция без ограничения Общий вид:
Двухфакторная функция без ограничения Общий вид:
 Появление ограничения. Появление Лагранжа. 2 типа задач: Постановка задачи: f(x 1, x 2) -> max p 1 x 1 +p 2 x 2 -> min при наличии ограничения: p 1 x 1 +p 2 x 2=V f(x 1, x 2) =U
Появление ограничения. Появление Лагранжа. 2 типа задач: Постановка задачи: f(x 1, x 2) -> max p 1 x 1 +p 2 x 2 -> min при наличии ограничения: p 1 x 1 +p 2 x 2=V f(x 1, x 2) =U
 1 задача: Строим функцию Лагранжа называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
1 задача: Строим функцию Лагранжа называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
 2 задача: Строим функцию Лагранжа все еще называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
2 задача: Строим функцию Лагранжа все еще называется множителем Лагранжа. выписываем условие первого порядка Система имеет, как правило, единственное решение
 Математическое ожидание
Математическое ожидание
 Спасибо за внимание. Домашнее задание будет выложена в группе ВК в 23 -59 (+-несколько минут) Также группа ВК перейдет в раздел закрытых.
Спасибо за внимание. Домашнее задание будет выложена в группе ВК в 23 -59 (+-несколько минут) Также группа ВК перейдет в раздел закрытых.
present5.com
Метод множителей Лагранжа - это... Что такое Метод множителей Лагранжа?
Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно ограничений , где меняется от единицы до .
Описание метода
- Составим функцию Лагранжа в виде линейной комбинации функции и функций , взятых с коэффициентами, называемыми множителями Лагранжа — :
Обоснование
Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.
Двумерный случай
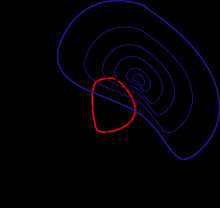 Линии уровня и кривая .
Линии уровня и кривая . Пусть требуется найти экстремум некоторой функции двух переменных при условии, задаваемом уравнением . Мы будем считать, что все функции непрерывно дифференцируемы, и данное уравнение задает гладкую кривую на плоскости . Тогда задача сводится к нахождению экстремума функции на кривой . Будем также считать, что не проходит через точки, в которых градиент обращается в .
Нарисуем на плоскости линии уровня функции (то есть кривые ). Из геометрических соображений видно, что экстремумом функции на кривой могут быть только точки, в которых касательные к и соответствующей линии уровня совпадают. Действительно, если кривая пересекает линию уровня в точке трансверсально (то есть под некоторым ненулевым углом), то двигаясь по кривой из точки мы можем попасть как на линии уровня, соответствующие большему значению , так и меньшему. Следовательно, такая точка не может быть точкой экстремума.
Тем самым, необходимым условием экстремума в нашем случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций и в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:
где — некоторое число, отличное от нуля, и являющееся множителем Лагранжа.
Рассмотрим теперь функцию Лагранжа , зависящую от и :
Необходимым условием ее экстремума является равенство нулю градиента . В соответствии с правилами дифференцирования, оно записывается в виде
Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению . Из нее можно найти . При этом , поскольку в противном случае градиент функции обращается в нуль в точке , что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки могут и не являться искомыми точками условного экстремума — рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.
На основе метода множителей Лагранжа можно доказать и некоторые достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.
Применение
См. также
Литература
- Зорич В. А. Математический анализ. Часть 1. — изд. 2-е, испр. и доп. — М.: ФАЗИС, 1997.
- Акулич И.Л. Глава 3. Задачи нелинейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9.
dic.academic.ru
3.2 Метод Лагранжа. Классические методы оптимизации
Похожие главы из других работ:
Багатокритеріальні задачі лінійного програмування в економіці
Графічний метод
Якщо модель містить тільки дві змінні, задачу можна розвязати графічно. У випадку трьох змінних графічний розвязок стає менш наочним, а при більшому числі змінних - взагалі неможливим. Незважаючи на це...
Изучение экономико-математических методов и их применения в управленческом учете
3. Метод дисконтирования
Чистый дисконтированный доход (Net Present Value, NPV) - это текущая стоимость денежных потоков инвестиционного проекта, с учетом ставки дисконтирования, за вычетом инвестиций...
Инструментальные средства управления территориально распределенными потоками заявок на транспортное обслуживание
1. Метод потенциалов
...
Использование среды MatLAB для решения линейной программы
2. СИМПЛЕКС-МЕТОД
...
Классические методы оптимизации
2.1 Правило множителей Лагранжа. Необходимые условия оптимальности
Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и при использовании обычных методов исследования функций, но при наличии ограничений типа равенств на независимые переменные...
Линейное программирование: методы решения задач
2.1 Графический метод
Графический метод решения задачи линейного программирования - основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач...
Линейное программирование: методы решения задач
2.2 Симплекс-метод
Двумерные задачи линейного программирования решаются графически. Для случая, когда неизвестны три переменные, можно рассмотреть трехмерное пространство...
Нахождение минимальных затрат при распределении товаров среди магазинов методами решения транспортной задачи
1.2.3 Метод потенциалов
Наиболее простым методом ТЗ является метод потенциалов. Потенциалами называются условные числа Ui ,Vj , приписанные определённым образом каждому поставщику и потребителю...
Оптимальный режим управления двухсекторной моделью экономики
3.1 Метод Эйлера
Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера...
Оптимизация транспортной работы, связанной с грузоперевозками, методами линейного программирования
1.3 Метод Моди
Для оценки оптимальности решения потенциалы подбираются следующим образом: потенциал первой строки берется равным 0, по расстоянию загруженных клеток подбирается потенциал для других строчек и столбцов таблицы...
Построение эконометрической модели. Проблема автокорреляции случайных отклонений
Тест Бреуша-Годфри (тест множителей Лагранжа)
Для устранения недостатков статистики Дарбина-Уотсона Бреуш (Breusch) и Годфри (Godfrey) разработали общий тест для обнаружения автокорреляции, который может применяться для высоких порядков авторегрессии случайных отклонений...
Предмет и метод эконометрики. Эконометрические взаимосвязи
1.1 Предмет и метод
Термин «эконометрика» впервые введен в Австро-Венгрии П. Цьемпой. Слово эконометрика это комбинация слов «эконом» и «метрика» т.е. экономика и измерение. Соответственно эконометрика это измерение в экономике...
Прогнозирование объема прибыли предприятия при наличии сезонной компоненты
1.2 Метод Четверикова
Эмпирический ряд выравниваетсяскользящей средней с периодом скольжения, т.е. берется (+1) членов исходного ряда, из которыхпервый и последний берутся с половинным весом:...
Разработка и исследование вероятностных эволюционных алгоритмов для моделирования и оптимизации сложных систем
1.1.1 Метод бинаризации
В общем виде задачу безусловной оптимизации можно представить в виде (1), где переменные могут быть выражены в различных шкалах измерений. ,(1) где - область изменения метрических переменных, - область изменения порядковых переменных...
Решение задачи о коммивояжере
Метод решения
Для начала следует сказать, что в основе любого метода решения данной задачи лежит полный перебор всевозможных вариантов путей. [2]Мы проходимся по каждому маршруту: одни отбрасываем, другие сравниваем с минимальным путем...
em.bobrodobro.ru
Метод множителей Лагранжа - это... Что такое Метод множителей Лагранжа?
Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно ограничений , где меняется от единицы до .
Описание метода
- Составим функцию Лагранжа в виде линейной комбинации функции и функций , взятых с коэффициентами, называемыми множителями Лагранжа — :
Обоснование
Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.
Двумерный случай
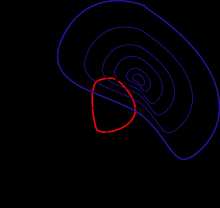 Линии уровня и кривая .
Линии уровня и кривая . Пусть требуется найти экстремум некоторой функции двух переменных при условии, задаваемом уравнением . Мы будем считать, что все функции непрерывно дифференцируемы, и данное уравнение задает гладкую кривую на плоскости . Тогда задача сводится к нахождению экстремума функции на кривой . Будем также считать, что не проходит через точки, в которых градиент обращается в .
Нарисуем на плоскости линии уровня функции (то есть кривые ). Из геометрических соображений видно, что экстремумом функции на кривой могут быть только точки, в которых касательные к и соответствующей линии уровня совпадают. Действительно, если кривая пересекает линию уровня в точке трансверсально (то есть под некоторым ненулевым углом), то двигаясь по кривой из точки мы можем попасть как на линии уровня, соответствующие большему значению , так и меньшему. Следовательно, такая точка не может быть точкой экстремума.
Тем самым, необходимым условием экстремума в нашем случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций и в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:
где — некоторое число, отличное от нуля, и являющееся множителем Лагранжа.
Рассмотрим теперь функцию Лагранжа , зависящую от и :
Необходимым условием ее экстремума является равенство нулю градиента . В соответствии с правилами дифференцирования, оно записывается в виде
Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению . Из нее можно найти . При этом , поскольку в противном случае градиент функции обращается в нуль в точке , что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки могут и не являться искомыми точками условного экстремума — рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.
На основе метода множителей Лагранжа можно доказать и некоторые достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.
Применение
См. также
Литература
- Зорич В. А. Математический анализ. Часть 1. — изд. 2-е, испр. и доп. — М.: ФАЗИС, 1997.
- Акулич И.Л. Глава 3. Задачи нелинейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9.
dal.academic.ru
Лагранжа метод множителей, оптимизация аналитическая
В простейших случаях, когда целевая функция задана аналитически, используют классические методы нахождения экстремума методами дифференциального исчисления. При наличии ограничений типа равенств, наложенных на независимые переменные, используют метод множителей Лагранжа. В более сложных случаях, когда критерий оптимальности представлен в виде функционалов, используют методы вариационного исчисления-, при оптимизации процессов, описываемых системами дифференциальных уравнений, применяют принцип максимума Понтрягина. Используют также динамическое, линейное программирование и другие методы оптимизации. [c.38] Аналитический метод оптимизации предусматривает аналитическое задание соответствующих функций и определение производных от них. На значения переменных, однако, могут накладываться ограничения, связанные с конструкцией, характером работы, стоимостью и т. п. В случае наличия таких ограничений, касающихся переменных величин, полезным может оказаться хорошо известный в математике метод множителей Лагранжа, [c.362]Для сложных реальных ситуаций метод множителей Лагранжа позволяет лишь сформулировать аналитически задачу оптимизации, а для нахождения оптимальных значений параметров необходимо применение поисковых методов. [c.178]
I. Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функций, заданных без ограничений, метод множителей Лагранжа, вариационные методы и принцип максимума. [c.247]
Пример 3 2 Решение задач оптимизации модели на основе уравнения регрессии методами классического аналитического поиска экстремума и Гаусса-Зейделя 76 Пример 3. 3 Расчет оптимальных размеров слоя катализатора в реакторе термокаталитической очистки отходящих газов от пргшесей углеводородов методом неопределенных множителей Лагранжа 79 Пример 3.4. Выбор рациональной схемы взаимного расположения аппаратов на базе [c.162]
Метод неопределенных множителей Лагранжа при решении задач оптимизации достаточно прост и удобен. Однако в более сложных случаях (например, при ненагруженном или облегченном резервировашш, при наличии нескольких ограничений и т. д.) его использование не всегда позволяет найти аналитическое решение и,поэтому приходится применять численные методы, из-за чего преимущества мегода множителей Лагранжа теряются. [c.774]
chem21.info