Исследование операций и методы оптимизации. Исследование операций и методы оптимизации
Содержание
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Самарский государственный аэрокосмический
университет имени академика С.П. Королева»
Б. А. ЕСИПОВ
МЕТОДЫ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Конспект лекций
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
С А М А Р А
Издательство СГАУ
2007
УДК 681.3.07
ББК 32.973.26-018.2.75
?К218

Рецензенты: докт. техн. наук, профессор А.Н. Коварцев
докт. физ-мат. наук, профессор С.Я. Шатcких
?К218 Есипов Б.А.
Методы оптимизации и исследование операций.
Конспект лекций: учеб. пособие / Б.А.Есипов. – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2007. – 180с. : ил.
??? ISBN 5-94774-0003-6
В учебном пособии дано краткое изложение основных методов оптимизации и исследования операций. Материал пособия основан на лекциях, читаемых автором для студентов факультета «Информатика» и соответствует программам курсов «Методы оптимизации», «Теория игр и исследование операций», «Теория принятия решений».
Настоящее пособие является вспомогательным материалом к прослушиваемому курсу лекций, поэтому применяется конспективный стиль изложения.
Приведены алгоритмы и примеры их работы, а так же рисунки, поясняющие суть методов, что позволяет студентам разрабатывать компьютерные программы для выполнения индивидуальных заданий курсовой работы.
Подготовлено на кафедре «Информационные системы и технологии» Самарского государственного аэрокосмического университета.
УДК 681.3.07
ББК 32.973.26-018.2.75
? ISBN 5-94774-0003-6 © Есипов Б.А., 2007
© Самарский государственный
аэрокосмический университет, 2007
1.Методология системного анализа и исследование операций 6
1.1. Системный анализ, система, оптимизация 6
1.2. Схема операционного проекта 7
1.3. Особенности математического моделирования операций 10
1.4. Постановка задачи исследования операций в детерминированном случае и в условиях неопределенности 11
1.5. Пример математического моделирования операции (Задача о краске). 12
2. Линейное программирование (ЛП) 16
2.1. Общая и основная задачи ЛП 17
2.2. Геометрическая интерпретация задачи ЛП 19
2.4. Симплекс-таблица, стандартный алгоритм симплекс-преобразования 23
2.5. Алгоритм отыскания опорного решения задачи ЛП 26
2.6. Алгоритм отыскания оптимального решения задачи ЛП 27
2.7. Алгоритм получения первого базисного решения с использованием симплекс – процедуры (метод искусственного базиса) 30
2.8. Вырожденная задача ЛП 33
2.9. Двойственная задача ЛП 33
3. Транспортные задачи (ТЗ) 36
3.1. Математическая модель ТЗ по критерию стоимости 36
3.2. Нахождение опорного плана транспортной задачи 37
3.3. Оптимизация плана ТЗ, распределительный метод 39
3.4. Метод потенциалов решения ТЗ 42
3.5. Решение ТЗ с неправильным балансом 45
3.6. ТЗ по критерию времени, типы критериев 48
4. Дискретное программирование 51
4.1. Особенности задач дискретного программирования 52
4.2. Примеры моделей задач дискретного программирования 53
4.2.1. Задача о покрытии 57
4.2.2. Задача о коммивояжёре 58
4.2.3. Задача о раскрое материала 59
4.2.4. Задача о ранце 61
4.3. Алгоритм решения задачи о ранце 62
4.4. Решение задач ЛЦП методом отсечений Гомори 65
4.5. Метод ветвей и границ (МВГ) 70
4.6. Алгоритм МВГ для задачи ЛЦП 72
4.7. Алгоритмы решения задач булевского программирования. 75
5. Динамическое программирование (ДП) 81
5.1 Принцип оптимальности Р.Беллмана 82
5.2. Решение графовых задач на основе принципа Беллмана. 84
5.3. Функциональное уравнение Беллмана 85
5.4. Задачи распределения ресурсов. 86
5.4.1. Классическая задача распределения ресурсов 86
5.4.2. Неоднородные этапы и распределение ресурсов по n отраслям 88
5.4.3. Распределение ресурсов с резервированием 88
5.4.4. Распределение ресурсов с “вложением доходов” 90
5.5. Расширение модели задач динамического программирования 92
6. Нелинейное программирование 99
6.1. Особенности задач нелинейного программирования 99
6.2. Прямые методы одномерной оптимизации нелинейных функций без ограничений 101
6.3. Градиентные методы многомерной оптимизации 103
6.3.1. Классический градиентный метод 103
6.3.2. Покоординатный метод 104
6.3.3. Метод наискорейшего спуска и его модификации 105
6.4. Метод деформируемого многогранника Нелдера-Мида 105
6.5. Задача НЛП с ограничениями-равенствами. 108
6.6. Выпуклое НЛП 110
6.8. Квадратичное программирование 113
6.9. Методы возможных направлений 118
6.10. Метод проекции градиента 122
6.11. Методы штрафных и барьерных функций 125
6.12. Метод скользящего допуска 131
7. Особенности современной теории принятия оптимальных решений 134
7.1. Общая постановка задачи принятия решения 135
7.3. Многокритериальная оптимизация 140
7.4. Определение множества Парето 143
7.5. Методы условной многокритериальной оптимизации 145
8. Игровые модели принятия решений 150
8.1. Основные понятия теории игр 150
8.2. Платежная матрица антагонистической игры, принцип минимакса 151
8.3. Решение игр в смешанных стратегиях 154
8.4. Упрощение игр и аналитическое решение игр 2*2. 154
8.5. Геометрическое решение игр 156
8.6. Решение игр с многими стратегиями на основе метода линейного программирования 160
8.7. Биматричные игры 162
8.8.Кооперативные игры 163
9. Элементы теории статистических оптимальных решений 165
9.1. Принятие решений при известных априорных вероятностях 166
9.2. Методы принятия решений в условиях априорной неопределенности 168
9.3. Планирование эксперимента при принятии решений 168
9.4. Многоэтапное принятие решений 171
10. Экспертные процедуры для принятия решений 174
10.1. Общая схема экспертизы 174
10.2. Задача оценивания 175
10.3. Подготовка экспертизы 175
10.4. Методы обработки экспертной информации 176
10.5. Метод Делфи для численной оценки 178
10.6. Строгое ранжирование 179
10.7. Нестрогое ранжирование 180
10.8. Метод попарных сравнений 180
Список литературы 182
studfiles.net
Исследование операций и методы оптимизации

Б.А. ЕСИПОВ
МЕТОДЫ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ.
КОНСПЕКТ ЛЕКЦИЙ
2007
САМАРА
Учебное издание
Есипов Борис Алексеевич
МЕТОДЫ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ.
КОНСПЕКТ ЛЕКЦИЙ
Учебное пособие
Редактор Компьютерная верстка Доверстка
Подписано в печать _________г. Формат 60х84 1/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. ____. Усл. кр.-отт.____.Уч.-изд.л.____ .
Тираж ____ экз. Заказ . Арт. С- ____/2007
Самарский государственный аэрокосмический университет.
443086 Самара, Московское шоссе, 34.
Изд-воСамарского государственного аэрокосмического университета.
443086 Самара, Московское шоссе, 34.
УДК 681.3.07 ББК 32.973.26-018.2.75К218
|
|
| И | ОНАЛ | Ь | Н |
| |
|
|
| Ц |
|
|
|
| |
|
| Н | А |
|
|
| Ы |
|
| Е |
|
|
|
| Е |
| |
|
|
|
|
|
|
| ||
Ы |
|
|
|
|
| П | ||
|
|
|
|
|
| Р | ||
Н |
|
|
|
|
|
| О | |
Т |
|
|
|
|
|
|
| Е |
Е |
|
|
|
|
|
|
| К |
Т |
|
|
|
|
| Ы | Т | |
|
|
|
|
|
| |||
Р |
|
|
|
|
| |||
И |
|
|
|
|
|
| ||
|
| О |
|
|
|
|
| |
|
|
| И |
|
|
|
|
|
|
|
| Р | П |
|
|
|
|
|
|
|
|
|
|
|
| |
Инновационная образовательная программа «Развитие центра компетенции и подготовка специалистов мирового уровня в области аэрокосмических и геоинформационных технологий»
Рецензенты: докт. техн. наук, профессор А.Н. Коварцев докт. физ-мат.наук, профессор С.Я. Шатских
К218 Есипов Б.А.
Методы оптимизации и исследование операций.
Конспект лекций: учеб. пособие /Б.А.Есипов. – Самара:Изд-воСамар. гос. аэрокосм.ун-та,2007.– 180с., 68 рис., 57 табл.
ISBN 5-94774-0003-6
В учебном пособии дано краткое изложение основных методов оптимизации и исследования операций. Материал пособия основан на лекциях, читаемых автором для студентов факультета «Информатика» и соответствует программам курсов «Методы оптимизации», «Теория игр и исследование операций», «Теория принятия решений». Настоящее пособие является вспомогательным материалом к прослушиваемому курсу лекций, поэтому применяется конспективный стиль изложения. Приведены алгоритмы и примеры их работы, а также рисунки, поясняющие суть методов, что позволяет студентам разрабатывать компьютерные программы для выполнения индивидуальных заданий курсовой работы.
Предназначено для студентов специальностей «Прикладная математика и информатика», «Автоматизированные системы обработки информации и управления», а также аспирантов и специалистов, интересующихся методами оптимизации и исследования операций.
Подготовлено на кафедре «Информационные системы и технологии» Самарского государственного аэрокосмического университета.
УДК 681.3.07 ББК 32.973.26-018.2.75
ISBN 5-94774-0003-6 | © Есипов Б.А., 2007 |
| © Самарский государственный |
| аэрокосмический университет, 2007 |
2
Оглавление |
|
Введение .............................................................................................................. | 6 |
1. Методология системного анализа и исследование операций........................ | 7 |
1.1. Системный анализ, система, оптимизация.......................................... | 7 |
1.2. Схема операционного проекта............................................................. | 8 |
1.3. Особенности математического моделирования операций ............... | 11 |
1.4. Постановка задачи исследования операций в детерминированном |
|
случае и в условиях неопределенности............................................ | 12 |
1.5. Пример математического моделирования операции (задача о |
|
краске)................................................................................................ | 13 |
2. Линейное программирование (ЛП)............................................................... | 16 |
2.1. Общая и основная задачи ЛП............................................................. | 17 |
2.2. Геометрическая интерпретация задачи ЛП....................................... | 19 |
2.3. Идея симплекс-методарешения задачи ЛП...................................... | 21 |
2.4. Симплекс-таблица,стандартный алгоритм симплекс- |
|
преобразования.................................................................................. | 23 |
2.5. Алгоритм отыскания опорного решения задачи ЛП......................... | 25 |
2.6. Алгоритм отыскания оптимального решения задачи ЛП................. | 26 |
2.7.Алгоритм получения первого базисного решения с использованием симплекс – процедуры (метод искусственного
базиса)................................................................................................ | 29 |
2.8. Вырожденная задача ЛП.................................................................... | 31 |
2.9. Двойственная задача ЛП.................................................................... | 32 |
3. Транспортные задачи (ТЗ)............................................................................. | 35 |
3.1. Математическая модель ТЗ по критерию стоимости........................ | 35 |
3.2. Нахождение опорного плана транспортной задачи.......................... | 36 |
3.3. Оптимизация плана ТЗ, распределительный метод.......................... | 38 |
3.4. Метод потенциалов решения ТЗ........................................................ | 40 |
3.5. Решение ТЗ с неправильным балансом............................................. | 43 |
3.6. ТЗ по критерию времени, типы критериев........................................ | 45 |
4. Дискретное программирование .................................................................... | 48 |
Особенности задач дискретного программирования............................... | 49 |
4.2. Примеры моделей задач дискретного программирования............... | 50 |
4.2.1. Задача о покрытии..................................................................... | 54 |
4.2.2. Задача о коммивояжёре............................................................. | 54 |
4.2.3. Задача о раскрое материала....................................................... | 55 |
4.2.4. Задача о ранце............................................................................ | 58 |
4.3. Алгоритм решения задачи о ранце.................................................... | 58 |
4.4. Решение задач ЛЦП методом отсечений Гомори............................. | 61 |
4.5. Метод ветвей и границ (МВГ) ........................................................... | 66 |
| 3 |
ВВЕДЕНИЕ
Одним из главных направлений деятельности специалиста в любой сфере является совершенствование существующих и создание новых изделий, систем или технологий: создание лучших машин, экономное расходование ресурсов, сокращение сроков строительства и т.д.
Обычно та или иная цель может быть достигнута разными путями, но всегда важно знать наилучший из них, так как в реальных условиях приходится считаться с ограниченностью материальных ресурсов и времени, расходуемых на достижение цели. Понятие «лучший» начинает что-либоозначать тогда, когда назван количественный показатель или критерий качества принимаемого решения. Например, изделие А лучше изделия В с точки зрения затрат материала; система С лучше системы D по показателю надежности и т.п.. Вот почему получение наилучших вариантов возможно только при количественном описании предметной области, т.е. на основе математической модели.
Методология анализа сложных систем, их математическое моделирование и нахождение на этой основе наилучших (оптимальных) решений в общем виде изучается в науке «исследование операций». В рамках этого общего направления изучаются и математические «методы оптимизации». Последнее название применяют для методов нахождения экстремумов функций и функционалов, когда математическая модель задачи уже сформулирована.
Большой вклад в развитие методологии исследования операций и методов оптимизации внесли российские и зарубежные ученые: Л.В.Канторович, Л.С.Понтрягин, Н.Н.Моисеев, Дж. Данциг, Г.Кун и А.Таккер, Р.Беллман, Р.Гомори и многие другие.
При подготовке рукописи этой книги использован опыт преподавания на факультете информатики Самарского государственного аэрокосмического университета. Это предопределило перечень вопросов, которые в первую очередь должны были быть освещены. При изложении автор предельно кратко старался излагать сугубо теоретические вопросы, оставляя место основным идеям и методам, имеющим универсальное значение. Особый акцент сделан на практические алгоритмы решения разнообразных задач, которые можно положить в основу разрабатываемых компьютерных программ.
6
1.МЕТОДОЛОГИЯ СИСТЕМНОГО АНАЛИЗА
ИИССЛЕДОВАНИЕ ОПЕРАЦИЙ
1.1.Системный анализ, система, оптимизация
Всередине двадцатого века во многих областях деятельности человека сформировалась необходимость изучения и совершенствования сложных систем, в том числе систем организационного типа: систем обороны; производственных систем, отраслей, предприятий и др.
Оказалось:
1)в сложных системах взаимосвязь между элементами играет большую роль, чем свойства самих элементов;
2)в таких системах элементы могут быть разнородны (оборудование, персонал, материалы, транспорт, условия поставок и сбыта и т.д.).
Термины системный анализ иисследование операций возникли, когда были образованы группы по исследованию военных операций в армии США
иАнглии во время второй мировой войны.
Кэтому времени, во-первых,был накоплен опыт применения математических методов для моделирования и решения некоторых задач экономики (В.Леонтьев, Л.В.Канторович), была теоретически обоснована возможность решения задач большой размерности на ЭВМ. Позже были созданы первые образцы таких машин. Совпали необходимость и возможность. Возникли новые идеи совершенствования организационных систем на основе математической теории игр (Нейман – Моргенштерн). Методология, сформулированная тогда и вобравшая в себя все научные достижения в области изучения сложных систем, оказалась применимой не только к боевым операциям, но и
кдругим сферам. Но термин «исследование операций» остался. Системный (операционный) подход – основа для изучения и совершенствования сложных систем. Применительно к специалистам - инженерам в области применения математики и информационных технологий в промышленности исследование операций формирует определенную технологию совершенствования существующих и создания новых систем как технических, так и организационных.
Система – множество элементов с определенными способами взаимодействия между ними, которые все вместе выполняютцель системы.
Процесс – все, что происходит в системе. Система работает, значит в ней происходит процесс.
Операция – часть процесса, которая наделена свойствами всей системы. Операция – это управляемое мероприятие, выполняющее определенную цель, сопоставимую с целью всей системы. Например,операция составле-
7
studfiles.net
Ответы на 2 модуль по предмету "ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ"
Ответы на 2 модуль по предмету "ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ"
1) Проверить выполнение баланса и привести транспортную задачу к виду, где условие баланса выполнено. Затем решить. Матрица стоимости перевозок имеет вид:Вектор запасов A =(120,85,75).Вектор заявок B =(90,70,60,80).Σ ai<Σ bj, F1=1740, F2 =1740
2) Сформулировать и решить транспортную задачу. Исходный опорный план найти методом минимального элемента. Матрица стоимости перевозок имеет вид:Вектор запасов A =(40,50,60)Вектор заявок B =(60,50,40,20,20)F1=1390, F2=1310
3) Перейти к двойственной и решить задачуf* = 3
4) Сформулировать и решить транспортную задачу. Исходный опорный план найти методом минимального элемента. Матрица стоимости перевозок имеет вид:Вектор запасов A =(35,40,40)Вектор заявок B =(25,25,55)F1=775, F2=700, F3=660, F4=655
5) Проверить выполнение баланса и привести транспортную задачу к виду, где условие баланса выполнено. Затем решить. Матрица стоимости перевозок имеет вид:Вектор запасов A =(45,35,70,60).Вектор заявок B =(40,35,55,60).Σ ai >=Σ bj , F1=1130(1490?), F2 =795
6) Фабрика производит два лака - для внутренних и наружных работ. Для производства лаков используется два исходных продукта - нефть и кислота. Максимально возможные суточные запасы для этих продуктов определяются емкостями их хранения и равны 6 и 8 тонн (т), соответственно. Для производства 1 т лака для внутренних работ расходуется 1 т нефти и 2 т кислоты, а для производства 1 т лака для наружных работ расходуется 2 т нефти и 1 т кислоты. Суточный спрос на лак для наружных работ не превышает 2 т. Спрос на лак для внутренних работ неограничен.Доход от реализации 1 т лака для внутренних работ равен 3 млн рублей, а доход от реализации 1 т лака для наружных работ - 2 млн рублей.Необходимо определить, какое количество лака каждого вида должна производить фабрика в сутки, чтобы доход от его реализации был максимальным.3x1 + 2x2→ max, x1 + 2x2≤ 6, 2x1+x2 ≤ 8, x2≤ 2, x1 ≥ 0, x2≥ 0
7) Фирма Лявон производит 2 типа деревянных игрушек: крестьяне (КР) и коровы (КО). КР продается за 27$ и требует материалов стоимости 10 $ и нематериальных расходов на сумму 14 $. КО стоит 21 $, требует материалов на 9 $ и нематериальных расходов в размере 10 $.Производство игрушек включает 2 типа работ: резьбу и окраску. КР требует 1 час резьбы и 2 часа окраски. КО требует 1 час резьбы и 1 час окраски.Каждую неделю Лявон получает все необходимые расходные материалы, но может использовать не более 80 часов для резьбы и не более 100 часов для окраски. Заказы на КР не превосходят 40 в неделю, а заказы на КО неограничены. Лявон желает максимизировать недельный доход (стоимость проданных игрушек минус расходы). Построить математическую модель и решить (x1 - КР, x2 - КО, z - целевая функция).x*1 =20, x*2 =60, z* = 180 $
8) Решить графически задачу линейного программирования видаf* = 5/2+3
9) Решить графически задачу линейного программирования видаf* = 10
Loading ...mtianswer.ru
Исследование операций и методы оптимизации
Эта точка получается как точка касания линий постоянного уровня величины F = (a1 −T1 )(a2 −T2 ) приF→max. Следовательно, решение такой игры дает супругам выигрыш (2,5; 2,5).
158
9. ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Это чрезвычайно развитая область в экономике, в военном деле, в области обработки информации на фоне шумов и т. д. Рассмотрим элементы этой теории как продолжение теории игр.
Существуют задачи, в которых B - «бессознательный игрок», который мешает нам принимать правильные решения, но он не противодействует активно, а действует в соответствии с природными случайными явлениями, поэтому такую ситуацию называютигрой с природой. Например, помехи в канале связи для передачи информации, шумы при записи или воспроизведении звука и т. д. Ясно что бессознательное воздействие в целом вредит нам меньше, чем сознательное. С другой стороны эта «бессознательность» приводит к непредсказуемому поведению операции. Можно считать ,что как и в теории игр мы боремся с противником, который не осознанно мешает нам. Например, это погодные условия, или случайный спрос при продаже товара. Вот почему в теории статистических решений, главной проблемой является обоснование принципов оценки различных ситуаций со стороныA. Заметим, что в теории игр был один принцип – принцип минимакса.
|
| Таблица 54 |
|
| P1 | P2 | Pn |
A1 | a11 | a12 | a1n |
A2 | a21 | a22 | a2n |
Am | am1 | am2 | amn |
Мы будем рассматривать дискретные альтернативы (стратегии) природы. Тогда, если у A имеетсяm стратегий, а у «природы» имеетсяn альтернатив, то может быть получена матрица выигрышей, при применении каж-
дой пары Ai Pj.
Условия Pj иногда называются гипотезами. Если платежная матрица построена, то задача состоит в анализе матрицы с целью получить стратегиюAi, которая наиболее выгодна по отношению к другим. В простейшем случае, есликакие-тостроки матрицы заведомо невыгодны, то их можно отбросить и оставить только одну, безусловно лучшую. Столбцы платёжной матрицы
159
нельзя отбрасывать, т. к. условия «природы» могут быть и в нашу пользу. При анализе платёжной матрицы можно сделать неверный вывод о качестве нашего решения.
Пусть сравниваются два выигрыша, находящихся в разных столбцах aij и
akl, причёмj≠l. Еслиaij>akl, то вроде бы решение вi- строке лучше, чем решение вk- строке, но так просто можно сравнивать, если выигрыш соответ-
ствует одинаковым условиям.
Пример: Пусть в Томской области, приняв определенные управляющие решения, получили урожайность пшеницы 20 центнеров с гектара, а в Краснодарском крае - 25. Эти значения сравнивать нельзя, т. к. для Томской области это может быть рекордный (наилучший) результат, а для Краснодарского края – плохой, т.к. рекорд 50 . Решение нужно сравнивать с потенциальными возможностями.
Вот почему необходимо преобразовывать платёжную матрицу таким образом, чтобы каждый наш выигрыш соотносился с тем максимумом, который можно достигнуть в данных условиях Pj Для каждогоPj можно найти максимальную величинуβj и вычислить величинуrij =βj -aij называемуюриском. Здесь
Чем риск меньше, тем лучше.
9.1. Принятие решений при известных априорных вероятностях
Будем обозначать вероятности гипотез: Q1=p(P1),Q2=p(P2), …,Qn=p(Pn). Таким образом, мы считаем, что вероятности известны до того, как мы решили принять решение.Решение - выбор оптимальной стратегииA. Говорят, что это ситуацияидеального наблюдателя.
Естественно, в качестве критерия выбирается средний выигрыш, который мы получим, если выберем стратегию Ai :
n
ai= ∑aijQj. j=1
Это аналог математического ожидания. Решение принимается по критерию:
Это критерий максимального среднего выигрыша. Если задана матрица рисков, то можно для каждой строки вычислить средний риск:
160
n
ri= ∑rijQj
j=1
иоптимальным будет являться решение, которое обеспечивает величину
Покажем, что оптимальное решение можно искать как по (9.1), так и по (9.2). Сложим средний выигрыш и средний риск получим константу
|
|
|
|
|
|
|
| n |
| n |
|
| n | n | n | |||||||
|
|
|
| + |
|
|
| = ∑aijQj+ ∑rijQj= ∑aijQj+ ∑(βj−aij)Qj= ∑βjQj= c , | ||||||||||||||
ai | ri | |||||||||||||||||||||
|
|
|
|
|
|
|
| i=1 |
| j=1 |
|
| j=1 | j=1 | j=1 | |||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
| + |
| = c |
| = c − |
| ; | max |
| = min |
| ; | arg max |
| = arg min |
| . | ||||
| ai | ri | ai | ri | ai | ri | ai | ri | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| i | i | |||
С – величина, не зависящая отi, это постоянная величина для данной строки.
В результате решения выбирается чистая стратегия ai. Есть ли смысл смешивать стратегии? Пусть мы смешиваем наши стратегии с вероятностямиpi, тогда в результате применения смешанной стратегии мы получим средний выигрыш в таком виде:
a = a1 p1 + a2 p2 +K+ am pm - математическое ожидание (МО).
Мы знаем, что МО меньше максимального значения, следовательно в игре с природой нет смысла смешивать стратегии; чистая стратегия обеспечивает наилучший результат. Слабым местом в этом подходе является то, что надо знать априорные вероятности. Если они неизвестны, то необходимо их изучить. Это можно делать путём экспериментов, которые изучают условия «природы». Говорят, что этим мы обучаем нашу систему. Такой подход называется принципом адаптации к условиям.
Если априорные вероятности изучить не удаётся, то применяется принцип недостаточности основания: если не знаем о вероятности, то считаем, что гипотезы природы равновероятны. После этого применяем критерий идеального наблюдателя. Так как при равных вероятностях энтропия (неопределённость) максимальна, то мы рассчитываем на худший случай , т.е.применяемпринцип пессимизма. Если сами значения вероятности неизвестны, но есть информация о предпочтениях гипотез, то существуют методы обработки предпочтений и получения вероятностей.
Если вероятности гипотез относятся как
161
n
n :(n −1):(n −2):K: 2 :1= Q1 :Q2 :K:Qn ;∑Qj =1 ,
j=1
то можно подсчитать саму величину вероятности в следующем виде:
Qj= | 2(n− j+1) | ; j = |
| . | |
1,n | |||||
n(n+1) | |||||
|
|
|
|
Внекоторых случаях учитывается не только средний выигрыш, но также
идисперсия, т. е. величина разброса выигрыша в каждой строке:
maxi (ai −k ×σai );σai = Dai .
9.2.Методы принятия решений
вусловиях априорной неопределенности
Если априорная информация неизвестна или ненадёжна, то применяются другие критерии.
Критерий Вальда (W): это максиминный критерий, т. е. выбирается стратегияAk, для которой
W = max minj aij .
i
При таком критерии мы подходим к этой задаче, рассчитывая на самый худший случай, как и в игре с разумным противником.
Критерий Сэвиджа (S): это критерий минимаксного риска
S = mini maxrij .
j
Этот критерий не эквивалентен критерию Вальда, т. е. cтратегия, оптимальная по Сэвиджу не обязательно так же будет оптимальна по Вальду.
Критерий Гурвица (H): это комбинированный критерий, его так же называют критериемпессимизма-оптимизма
H = maxi (κ minj aij +(1−κ )maxj aij );
где 0 <κ <1 - коэффициент, который выполняет требования критерия быть более или менее оптимистичным. Приk=1 критерийH=W, а приk=0 получаемкрайний оптимизм.
Существуют другие критерии и однозначный выбор одного критерия невозможен. Но если одну и ту же ситуацию рассматривать по разным критериям и
162
получаются одинаковые решения, то это говорит об устойчивости данной ситуации и однозначности найденного оптимального решения. В противном случае ситуация неустойчивая и необходимо либо изучать априорную информацию, либо доказывать верность лишь одного из критериев.
9.3. Планирование эксперимента при принятии решений
Если априорной информации нет или она ненадёжна, то можно путём проведения эксперимента получить более надёжные данные о вероятностях Qj. Подэкспериментом понимают систему мероприятий позволяющих уточнить информацию о состоянии «природы». Например, это метеонаблюдения, маркетинговые исследования в экономике, радиолокация, военная или промышленная разведка и т.д. Насколько может помочь в принятии решения эксперимент и как сопоставить стоимость эксперимента с тем оптимальным выигрышем, который мы получим?
Соответствующую теорию можно построить исходя из знания вероятно-
стей Qj , а так же на основе критериев при неизвестной априорной информации. Мы рассмотрим случай, когда есть априорная информация, т. е. ситуацию идеального наблюдателя. Рассмотрим вопрос: есть ли смысл проводить эксперимент? Рассмотрим два случая.
1) Идеальный эксперимент. Результат этого эксперимента однозначно определяет каковы условия природы. Пусть заданы выигрышиaij и априор-
ные вероятности Qj. Стоимость экспериментас сопоставима с выигрышемaij, т. е. эти величины имеют одинаковую размерность. Сравним средний выигрыш без проведения эксперимента со средним выигрышем при проведении эксперимента:
Если нет эксперимента, мы обеспечим себе
|
| n |
|
|
|
|
max | ∑aijQj | = |
| . | ||
amax | ||||||
i |
| i=1 |
|
|
|
|
Если мы проведём эксперимент, то мы точно узнаем Pj =Pk, и тогда найдя вk-мстолбце максимальный выигрыш, мы найдём наш выигрыш
max aij = βk .
i
Но нам нужно оценить эффективность эксперимента до его проведения, поэтому мы должны ориентироваться на средний ожидаемый выигрыш, который мы получим, если будем проводить эксперимент. Таким образом, перед проведением эксперимента мы можем ожидать выигрыш
163
n
∑Qj×βj .
j=1
Поэтому чтобы решить, проводить эксперимент или нет, надо определить, что больше: amax или
n
∑Qj×βj .
j=1
Получается, что необходимо проводить эксперимент, если
n |
| n |
∑Qjβj | −c > max∑Qj aij . | |
j=1 | i | j=1 |
| ||
Преобразовав это неравенство, получим, что идеальный эксперимент проводить нужно, если его стоимость меньше минимального среднего риска
c < mini ri .
2) Неидеальный эксперимент. В результате проведения неидеального эксперимента мы не находим однозначноPj, а лишь изменяем вероятностиQj. Пусть проводится неидеальный эксперимент. В результате появляются некоторые несовместные событияB1,B2,…BL. Вероятности этих событий зависят от условий, в которых они проводятся. Пусть известныP(Bj/Pj). Эти вероятности называютсяпрямыми. После эксперимента, давшего исходBl необходимо пересмотреть вероятностиQj, т. е. вместо вероятностиQj мы перейдём к вероятностиQjl. Это так называемыеапостериорные вероятности
| = P(Pj | Bl)= | Qj ×P(Bl | Pj) | − | |
Qjl | ||||||
n | Pj)) | |||||
|
|
| ∑(Qj ×P(Bl |
| ||
|
|
| j=1 |
|
|
Это формула Байеса.
Но результаты эксперимента могут быть и B1 иB2 иBk, поэтому мы можем только ожидать всякие исходыBl, которые получатся в результате эксперимента. Причём, каждый исходBl привёл бы к некоторым оптимальным стратегиямA*1. А величина выигрыша, которая бы при этом получилась:
n
a%l = maxi a%il = maxi ∑j=1 (Q%jl ×aij ).
164
Эти выигрыши a%l , могут произойти с вероятностью событияBl, т. е. c вероятностью.P(Bl), которую можно получить по формуле полной вероятности:
n
P(Bl)= ∑QjP (BlPj).
j=1
Тогда средний ожидаемый выигрыш будет:
k
a% = ∑l=1 al P(Bl ) a%−c> maxi ∑Qj aij a%−c> amax .
Планирование экспериментов можно рассмотреть и для случаев, когда проводят 2, 3, 4, … эксперимента [8].
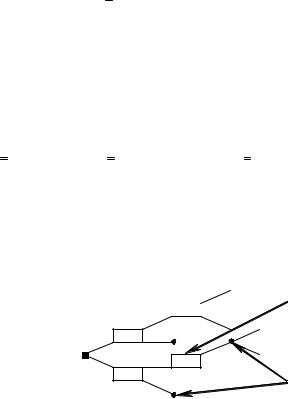
9.4. Многоэтапное принятие решений
Сознательное
принятие решения
Случайная
вершина
Рис. 66
Мы рассмотрели различные критерии принятия решений в условиях неопределённости. На практике, в таких задачах как проектирование изделий, управление процессами, создание сложных программных комплексов, мы можем столкнуться с принятием последовательных решений (цепочкой решений).
Особое значение такие многоэтапные решения имеют при создании автоматизированных экспертных систем. Рассмотрим вопрос оптимизации многоэтапных решений. Многоэтапность приводит к тому, что схема принятия решения может быть представлена в виде дерева, в каждой вершине которого осуществляется:
1)Сознательный выбор между двумя и более альтернативами
2)Либо случайный переход из одной ветви в другую под воздействием внешних случайных факторов.
Рассмотрим пример оптимизации многоэтапных решений на примере экономической задачи.
165
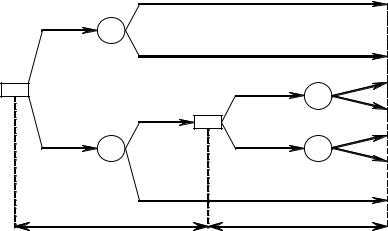
Пример. Фирма может принять решение о строительстве крупного или мелкого предприятия. Строительство крупного предприятия относительно дешевле, в случае если будет высокий спрос на производимые товары, мелкое предприятие можно расширить. Деятельность фирмы рассматривается в течение десяти лет, причём в случае строительства мелкого предприятия вопрос о расширении будет рассматриваться через два года. Спрос заранее неизвестен.
|
| p=0,75 |
|
| 1,0 |
|
|
|
|
| |
крупное | 2 |
|
|
|
|
|
|
|
|
| |
|
| p=0,25 |
|
| 0,3 |
|
|
|
|
| |
1 |
|
| расш | p=0,75 | 0,9 |
|
| 5 |
| ||
|
|
|
| 0,2 | |
|
| p=0,75 | 4 | p=0,25 | |
|
|
|
| ||
|
|
| p=0,75 | 0,25 | |
мелкое |
|
| без расш. | ||
3 |
| 6 |
| ||
|
|
| 0,2 | ||
|
|
|
| p=0,25 | |
|
| p=0,25 |
|
| 0,2 |
|
|
|
|
| |
| 2 года |
| 8 лет |
|
|
Рис. 67
Введём градацию случайного спроса: высокий (p>0,75) и низкий (p<0,25). Затраты и доходы: строительство крупного предприятия - 5 млн. $; строительство мелкого - 1 млн. $; затраты на расширение - 4,2 млн. $; крупное предприятие при высоком спросе даёт доход - 1 млн. $ ежегодно, а при низком - 300 тыс. $; мелкое предприятие при высоком спросе - 250 тыс. $ ежегодно, при низком - 200 тыс. $; расширенное предприятие в случае высокого спроса приносит доход - 900 тыс. $ в год, и при низком спросе - 200 тыс. $; мелкое предприятие без расширения при высоком спросе на производимый продукт приносит в течение двух лет по 250 тыс. $ ежегодно, а в течение следующих восьми по 200 тыс. $. Нарисуем дерево решений.
Применим для решения этой задачи метод динамического программирования. В качестве критерия применим средний выигрыш, т. е. МО выигрыша. Сама величина критерия равна доходу без затрат на строительство. Начнём с последнего четвёртого шага, подсчитаем средний выигрыш:
166
aрасш4 = (0,9*0,75+ 0,2*0,25)*8− 4,2=1,6 ,aбез4 расш = (0,25*0,75+ 0,2*0,25)*8=1,9 ,aкруп1 = (1*0,75+0,3*0,25)*10−5,0= 3,25 ,
aмелк1 = (1,9+ 2*0,25)*0,75+0,2*10*0,25=1,3 .
Исходя из полученного результата, оптимальным будет сразу строить крупное предприятие.
Другим примером оптимизации многоэтапных операций является известная «задача о секретарше».
Директор собирается принять на работу секретаршу. Прежний опыт делит секретарш на три категории: отличных (3 балла), хороших (2 балла) и посредственных (1 балл). Анализ учебных заведений по подготовке секретарш даёт статистику выпускниц заведений: вероятность взять на работу отличную секретаршу - 0,2, хорошую - 0,5, посредственную - 0,3. директор может испытать только трёх претенденток, причём в случае отказа директора кандидат убывает на другую работу. Построим дерево решений.
|
|
|
|
|
|
|
| p=0,2 |
|
| stop |
| p=0,2 |
|
| stop | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| p=0,2 |
|
|
| stop |
|
|
|
|
| a=3 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| a=3 |
|
| p=0,3 |
|
| продолжить | 3 | p=0,3 |
|
| stop | ||
|
|
|
|
|
|
|
|
|
|
| ||||||||
1 | p=0,3 |
|
|
| продолжить | 2 |
|
| stop |
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| stop |
|
|
|
|
| a=1 |
| p=0,5 |
|
| stop | ||
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
| a=1 |
| p=0,5 |
|
| продолжить |
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| p=0,5 |
|
|
| продолжить |
|
|
| stop |
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
| stop |
|
|
|
|
| a=2 |
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| a=2 |
|
|
|
|
|
|
|
|
|
|
|
| |
Рис. 68
В соответствии с процедурой динамического программирования начнём искать оптимальное решение с последнего шага. Определим математическое ожидание «выигрыша», если мы испытываем третьего кандидата:
a3 = 3*0,2+ 2*0,5+1*0,3=1,9 .
Далее определим средний выигрыш, если мы испытываем второго и третьего, с учетом того, что если второй будет посредственный, то мы продолжим и получим в среднем 1.9.
a2 = 3*0,2+ 2*0,5+1,9*0,3= 2,17 .
167
studfiles.net
Исследование операций и методы оптимизации

1.Безусловная оптимизация. Здесь анализируется критериальное пространство, отсеиваются безусловно худшие варианты и получают множество Парето.
2. Условная оптимизация. Так как множество Парето, как правило, состоит из более чем одной точки, то для получения единственного решения необходимо применить дополнительные принципы оптимальности (условия согласования критериев).
7.4. Определение множества Парето
Если целевая функция векторная функция векторного аргумента и каждому малому изменению переменных X соответствует малое изменение каждого критерия, то критериальное пространство – это область с внутренними точками и границей. (не обязательно замкнутая). Пусть есть только два кри-
терия (k1,k2) иk1 Æ max;k2 Æ max.
K2 | C 3 |
| Рассмотрим область возмож- |
| ных значений критериев (рис. 54). | ||
| A |
| |
|
| Ясно, что точки, лежащих на од- | |
| 2 | B | ной вертикали или на одной гори- |
| 1 | ||
|
| зонтали всегда, безусловно срав- | |
|
|
| |
| D |
| нимы (точки 1, 2, 3). Получается, |
|
| что все внутренние точки можно | |
|
|
| |
|
| K1 | отсеять. Дуга АВ состоит из луч- |
| Рис. 54 |
| ших точек по критерию k2 при по- |
стоянном k1.
Но часть точек дуги АВ , а именно точки дуги AС можно отбросить, так как они хуже точек СB. Поэтому точками множества Парето будут являться точки, находящиеся на дуге CB. При анализе характерными являются точки касания вертикалей и горизонталей к области критериев (точки А, В, С, D).
Существует несколько алгоритмов нахождения множества Парето. Они зависят от того, в каком виде задано множество вариантов критериев. В практических задачах сначала приходится получать само множество критериев, затем получать множество Парето в критериальном пространстве и только затем можно определить Парето-оптимальноемножество в области допустимых решений X.
Существуют два основных метода нахождения множества Парето: Метод обхода конусом. Этот метод применяется для непрерывной области
критериев. Назовем конусом пространственный угол, образуемый лучами, идущими из общей вершины и ограниченными в каждой плоскости углом 90°. Направление ограничивающих лучей соответствует направлению оптимизации критериев.
138
Отформ
ширине, строка: нумерац висячих
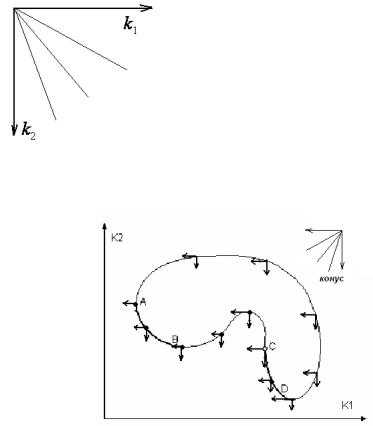
Рис. 55
Пример: k1 → min,k2 → min
Пусть для двух критериев: k1Æ max (↑) иk2 Æ min (↓), тогда конус имеет вид, изображенный на рисунке 55.
Для получения множества Парето достаточно установить вершину конуса на все точки границы области критериев, если при этом ни один луч не пересекает область, то вершина лежит в точке Парето, а если пересекает, то нет.
Рис. 56
Множество Парето: [AB] (CD]
2.Метод прямоугольников. Этот метод применяют, когда критериальное пространство представляет собой отдельные точки или табличные значения. Сформулируем алгоритм для случая двух критериев, когдаk1→min иk2→min, а критериальное пространство – точки на плоскости.
1)Фиксируем самые левые точки, если их несколько, выбираем среди них самую нижнюю. Эта точка является точкой Парето, фиксируем ее.
2)Выберем самую нижнюю точку, если их несколько, то выбираем самую левую. Это точка Парето, фиксируем ее.
3)Через полученные точки проводим вертикаль и горизонталь. Отбрасываем сами точки Парето, точки лежащие на границе полученного прямоугольника и точки вне прямоугольника.
4)К внутренним точкам полученного прямоугольника применяем алгоритм из пункта 1.
139
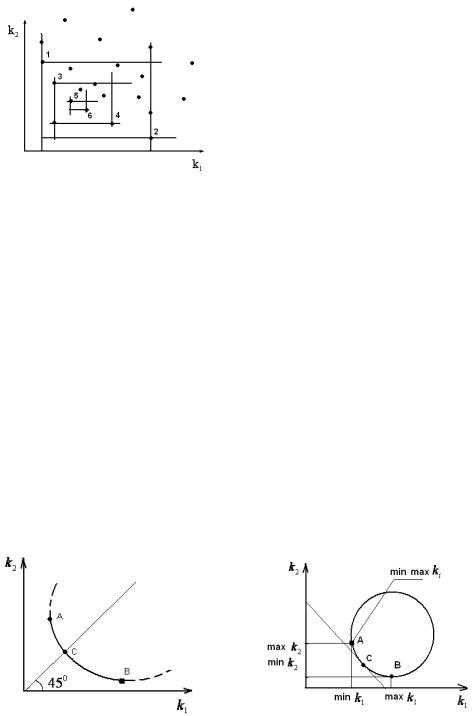
| Алгоритм заканчивается то- | ||
| гда, когда внутри прямоугольника | ||
| не останется ни одной точки. | ||
| Множество Парето: | ||
| 1, 2, 3, 4, 5, 6. |
| |
| Вышеизложенный | алгоритм | |
| легко | обобщается | на случай |
| большего числа критериев, при | ||
| других | направлениях | оптимиза- |
| ции, а также на случай табличного | ||
Рис. 57 | задания критериев. |
| |
7.5. Методы условной многокритериальной оптимизации
После нахождения множества Парето, если количество точек в нём ≥2, встаёт вопрос о выборе единственного решения. Так как точки на множестве Парето обладают таким свойством, что каждая из них лучше по одному критерию, но хуже по другому, то объективно предпочесть эти точки невозможно.Условная оптимизация предполагает введение условия согласованности в компонентах критерия, которое всегда является хотя и разумным, но субъективным. Подобные условия еще называют схемой компромиссов. Рассмотрим несколько простейших из них.
Принцип равенства критериев. Рассматривают множество Парето для стандартных критериев. Тогда оптимальной считается та точка множеств Парето, гдеk1=k2=…=kL (см. рисунок 58).
Принцип равного влияния. Здесь оптимальной считается точка множества Парето, являющаяся точкой касания прямойk1+k2Æ min и области Парето (точкаС, см. рисунок)
Принцип минимакса. Оптимальной считается точка множества Парето, где обеспечивается minmaxkiст. (см. рисунок 5).
Кроме указанных простейших приемов применяются более сложные.
140
1) Метод скаляризации. Здесь формируется некоторая скалярная функция многих переменных:
K0 = f(K1, K2 ,K, KL ).
K0 - это скалярная величина, которая обобщает все критерии. Наиболее распространённой разновидностью функцииf является линейная функция
L
K0 = ∑αi Ki → min(max)
i=1
ai -вескаждой компоненты критерия, чем эта величина больше, тем большее влияние оказывает этот критерий. Для нестандартных критериев веса могут иметь размерность, причем еслиKi→max, тоai≥0, а когдаKi→min, тоai≤0. Подобная комплексная оценка зачастую затруднительна. На практике часто используют и другие способы искусственного объединения нескольких показателей в один обобщённый показатель (критерий). В качестве обобщённого критерия, например, берут дробь:
K0=(k1×k2×...×km) /(km+1×…×.kL ),
где k1 ... km – увеличиваются,
km+1.. kL - уменьшаются.
Вольное использование подобных критериев чревато опасностями и может привести к неправильным рекомендациям.
Общим недостатком «составных критериев» является то, что недостаток эффективности по одному показателю всегда можно скомпенсировать за счёт другого (например, малую вероятность выполнения боевой задачи – за счёт малого расхода боеприпасов и т.п.).
На этот счет известна шутка Л.Н.Толстого, что если представить оценку человека в виде дроби:
Достоинствочеловека, то можно получить самую высокую оценку в
Мнениеосебе
случае | Малодостоинств | = ∞ . |
| Нет мненияосебе |
|
2) Метод главного критерия. В этом методе сначала выбирают главный критерий и объявляют его единственным критерием. Все остальные критерии становятся управляемыми переменными, на которые накладываются ограничения, что бы они были не хуже заданной величиныki0. Например, если всеki Æ min и главныйk1, то получаем однокритериальную задачу математического программирования
k1 = f ( X)–>min,
141
Фi (X) < 0, i = 1,2,3,…m,
k2 (X)<k20 , k3(X)<k30 , … , kL(X)<kL0 .
Тогда, эти ограничения войдут в комплекс заданных условий. Например, в промышленности можно потребовать, что бы прибыль →
max, план по ассортименту – выполнен, а себестоимость – не выше заданной. При бомбардировке – понесённый ущерб противника максимальный, по-
тери и стоимость операции не выходили за известные пределы.
Здесь все показатели эффективности, кроме одного, переводятся в разряд ограничений. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются как недопустимые.
Такой метод чаще всего используется при оптимизации сложных технических систем (самолетов, автомобилей, бытовой техники и т.д.).
3). Метод последовательных уступок. Проранжируем все критерии и расположим их в порядке убывающей важности:k1, k2 …. kL.. Пусть все критерии нужно максимизировать. Сначала отбросим все критерии, кромеk1 и найдем допустимое решение, обращающее в максимумk1 . Как правило при этом другие критерии не получают своих наилучших значений. Поэтому исходя из практических соображений и точности, с какой известны исходные данные, назначается уступка⌂k1 , которую мы согласны допустить для того, чтобы обратить в максимум k2 . Наложим наk1 ограничение, чтобы он был не меньше чемk1*- ⌂k1 (k1* - максимально возможное значениеk1), и при этом ограничении ищем решение, обращающее в максимумk2. Далее снова назначается уступка в показателеk2, ценой которой находится максимумk3 и т.п.
k2 → max,
k1max− k1< k1< k1max.
На втором этапе решаем задачу
k3 → max,
k1max− k1< k1< k1max, k2max− k2< k2≤ k2max.
И так далее.
Такой способ хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом. Заметим, что иногда даже при малом ⌂k «свобода» выбора позволяет достичь существенной оптимизацииk2 . Это зависит от вида границы критериального пространства (см. рисунок 60).
142
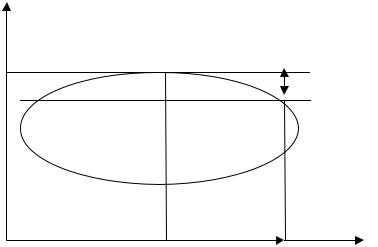
F→max
k 1 max
⌂ k1
Очевидно, успех такого метода зависит от того, насколько «тупой» максимум. Процедура может быть повторена для других K.
4. Метод последовательной оптимизации. В некоторых случаях критерии системы не слишком связаны друг с другом, т.е. улучшение одного критерия, по крайней мере в ограниченных пределах, не «мешает» другому. Это характерно для сложных систем, состоящих из отдельных достаточно автономных подсистем (например: процессор компьютера, система электропитания, система охлаждения, система отображения), когда отдельные критерии относятся к этим подсистемам. Расположим все критерии в порядке убывания важности. Сначала оптимизируют систему по важнейшему показателю, отбросив все остальные, затем по второму, и т. д.
Следует отметить, что в вышеприведенных методах используется процедура упорядочения критериев по важности. Эта самостоятельная проблема является достаточно сложной и поэтому решается на основе методов экспертных оценок, изложенных в 10-йглаве.
143
8. ИГРОВЫЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ
Математические модели, рассмотренные нами, выражают стремление получить максимальный результат для какой-тоодной системы (фирмы, отрасли, страны). Если эта система состоит изкаких-тодругих элементов (подсистем), то считается, что их целевые функции совпадают, то есть эти подсистемы работают «все как один». Во многих задачах это не так. Приходится анализировать ситуации, когда присутствует несколько сторон, преследующих различные интересы (цели). Это и боевые действия, и внешняя экономическая деятельность государств и многое другое. При переходе к рыночной экономике и возникновении конкуренции как основного рычага развития экономики постановка задачи с отождествлением целей является неполной, а иногда и неправильной. Интересы отдельных фирм сталкиваются на одном рыночном пространстве и иногда настолько различны, что конкуренция приобретает форму борьбы, и поэтому невозможно оценить результат принимаемого решения единообразно. Такого рода ситуации называютсяконфликтными и могут быть описаны моделями, которые называютсяиграми. Модели конфликтных ситуаций, где присутствуют несколько сторон, преследующих различные интересы, называютсяигровыми моделями. Игровая модель представляет собой особый вид модели для принятия оптимальных решений. Теория, описывающая конфликтные ситуации с количественной стороны, называетсятеорией игр.
8.1. Основные понятия теории игр
Игра – математическая модель ситуации, некоторая упрощённая схема, где зафиксированы все участвующие стороны, правила развития данной ситуации, определённые выигрыши после каждого хода, правила окончания игры. Из этого следует, что основными в игровой модели являются следующие элементы:
•в игре могут быть две или более стороны, называемые игроками,кото-рые преследуют различные интересы;
•в игре фиксируют правила игры: возможные действия игроков, ситуация выигрыша и его величина, правила остановки игры;
•игры бывают парные, когда есть только две стороны, имножественные, когда участие в игре принимают три и более сторон;
•игры бывают коалиционные, когда часть игроков соединяют свои ин-
тересы и действуют как один игрок.
Мы рассмотрим только парные игры как наиболее важные для моделирования реальных явлений. Результаты анализа таких моделей позволяют сформулировать принципы и подходы к выработке оптимальных решений в условиях конкуренции.
Отформ
Отступ: Выступ: маркиро Уровень по: 14,2
после: 5 0 пт, Поз
5,65 пт
В парной игре два игрока: A – это «мы» и B – «противник». Игры называются антагонистическими, или спротивоположными интересами, если игрок A выигрывает ровно столько, сколько проигрывает B. В сумме выигрыш равен 0, поэтому такую игру называют игрой с нулевой суммой. Но существуют также парные игры и с ненулевой суммой (неантагонистические).
Ходы в игре могут быть личные ислучайные. Личный ход зависит от сознательного решения стороны, а случайный ход - результат случайного механизма, который иногда применяется специально, а иногда случайно вовлекается в игру. В ходе проведения игры каждый игрок имееткакие-тоальтернативы поведения, которые называютстратегиями игроков. В общем случае стратегия игрока – это совокупность правил, определяющих выбор вариантов действий при каждом личном ходе игрока в зависимости от сложившейся ситуации. Применение в каждой игре стратегии однозначно определяет исход игры. Если количество стратегий конечно -игра конечная, в противном случае -бесконечная игра. В теории игр считается, что игра повторяется многократно и игроков интересует средний выигрыш. Задачей теории игр является обоснование оптимальных стратегий обоих игроков.
8.2. Платежная матрица антагонистической игры, принцип минимакса
Будемсчитать, чтоуигрокаA всегоm стратегий, ауигрокаB –n стратегий. A1A2 ..........Am
B1B2 ...........Bn
Таблица 41
| B1 | B2 | . | Bn |
А1 | a11 | a12 |
| a1n |
А2 | a21 | a22 | . | a2n |
. | . | . |
|
|
Аm | am1 | a11 | . | amn |
Если игрок А применяет свою стратегию Аi, а В применяет Bj, то выигрыш в игре составляетaij. А старается увеличивать выигрыш, а В – уменьшить эту величину. Величиныaij образуют матрицу, которая называетсяплатежной матрицей .
Рассмотрим пример простейшей игры «Поиск». |
|
|
| |
Игрок А прячется в двух местах I |
| Таблица 42 |
| |
и II. Игрок В ищет игрока А в местах I |
|
| ||
|
|
|
| |
и II. Если В находит А, то А платит |
|
|
|
|
ему 1 рубль, если не находит, то В |
| B1 |
| B2 |
А1 | -1 |
| 1 | |
платит 1 рубль игроку А. |
| |||
А2 | 1 |
| -1 | |
Платежная матрица – Таблица 42. |
| |||
|
|
|
| |
145
Основой для анализа игр является анализ платежной матрицы. Поэтому игры, для которых могут быть построены платежные матрицы, называются матричными играми.
Для игр с полной информацией, т. е. когда один игрок знает, как поступил второй, всегда можно построить платёжную матрицу.
Основным принципом, которым необходимо пользоваться для объективной оценки игровой ситуации, является следующий подход: противник настолько же разумен, как и мы, и делает все, чтобы использовать свои возможности против нас, т. е. активно противодействует в выборе оптимального решения. Задачей теории игр является обоснование оптимальных стратегий обоих игроков.
Если игрок А будет применять любое сколь угодно сложное правило чередования мест I и II, то В все равно разгадает этот закон чередования и будет выигрывать. Ниже мы обоснуем оптимальные стратегии игроков А и В. Рассмотрим другие простые примеры игр.
Игра «Три пальца».
Таблица 43
| B1 | B2 | B3 |
А1 | 2 | -3 | 4 |
А2 | -3 | 4 | -5 |
А3 | 4 | -5 | 6 |
Игра «Конкуренты».
Таблица 44
| B1 | B2 | B3 |
А1 | -2 | -2 | 1 |
А2 | 1 | 0 | 2 |
А3 | 0 | -1 | 1 |
Игрок А и игрок В одновременно показывают один, два или три пальца. Выигрыш равен сумме, причём выигрывает А, если сумма очков четная, и В, если сумма нечетная. Построим платёжную матрицу.
Фирма А может поставить на рынок три товара A1, A2, A3, а фирма В три своих конкурирующих товара B1, B2, B3. Если фирма А поставит товар Ai, а фирма В - товар Bj, то в результате выигрыш в доходах фирм определяется приведенной платежной матрицей.
Возникает вопрос – как на основе анализа матрицы найти оптимальное решение игры, и что понимать под оптимальным решением игры?
Рассмотрим так называемый принцип минимакса при решении игры. Ясно, что игроки должны действовать с разумной осторожностью, т. е.
необходимо, чтобы мы больше всего реагировали на опасные для нас ходы со стороны противника. По отношению к игроку А рассуждаем так, что если он применит стратегию A1, то можно зафиксировать самый плохой для него выигрыш:a1 = minaij.
146
Для стратегии A2:a2 = mina2j.,и так далее.
Для Am:am = minamj.
Тогда естественно, что игрок А выберет ту стратегию, для которой величина ai будет максимальной (по строкам в платежной матрице).
Величина a = max minaij называетсянижней ценой игры. Она показыва-
i j
ет, меньше какой величины не будет выигрыш игрока А при осторожном подходе к игре. Аналогично рассуждая относительно игрока В, получаем величины:
bj = maxaij - максимальные величины в столбцах, и затем
b = max minaij -верхняя цена игры.
i j
Эта величина показывает, больше какой величины не может быть выигрыш в игре.
Получим значения a иb для вышеприведенных игр. Для игры «Поиск»a =-1;b =1.
Для игры «Три пальца» a =-3;b =4. Для игры «Конкуренты»a =b =0.
Эта игра обладает седловой точкой, так как в ней максимин совпадает с минимаксом. Принятие стратегий, соответствующих седловой точке, взаимоприемлемо для обоих игроков, поэтому их можно принять за оптимальное решение игры. Таким образом, пара стратегий (A2, B2) является оптимальным решением игры «Конкуренты». Оптимальный выигрыш в этой игре называетсяценой игры и равен 0.
Если игра имеет седловую точку, то говорят, что игра решается в чистых стратегиях. Решение, соответствующее седловой точке, обладает свойством устойчивости:если один игрок примет оптимальную стратегию, то другому невыгодно отклоняться от своей оптимальной стратегии. (Проверьте это, рассмотрев строку A2 и столбец B2). Такое свойство устойчивости положено в основу понятия оптимального решения любой игры.
8.3. Решение игр в смешанных стратегиях
Если в игре верхняя и нижняя цена не совпадают ( a не равноb ), то значит, что седловой точки нет, но можно улучшить средний выигрыш игроков А и В путем смешивания их стратегий. Это значит, что игрок А, каждый раз играя игру, чередует свои чистые стратегии A1A2 ..........Am . Вопрос состоит
в том, какова должна быть доля случаев применения стратегий игроков. Назовем смешанной стратегией игрока А вектор SA = (p1 , p2 ,K, pm ), в
котором показаны вероятности применения соответствующих стратегий. На-
пример: SA | m | - свойство полноты. |
= (0,1; 0,2; 0,7; 0),∑pi =1 | ||
| i=1 |
|
147
studfiles.net
Исследование операций и методы оптимизации
Летательный аппарат находится на высоте h0 и летит со скоростьюv0. Необходимо перевести его на высотуh2 со скоростьюv1. Причёмh0>h2, v0>v1. Разобьём участок отh0 доh2 наn частей:
h = h2−n h0, v = v1m−v0.
Известен расход горючего при переводе системы на h приv=const и наv приh=const. Таким образом, из каждого состояния есть лишь два управления.
Начиная с конца помечаем все узлы (состояния) величинами условных (для данного узла) оптимальных расходов горючего от этого узла и до конца, a стрелками условные оптимальные управления. Указанные действия в упрощенном виде демонстрируют рассмотренную процедуру решения на основе уравнения Беллмана. Дойдя от конечного состояния до начального и получив 22, мы получим минимальную величину потерь горючего. Идя по стрелкам от начального состояния до конечного, мы получаем безусловные оптимальные управления (показаны двойной линией).
Видно, что любая задача, сводящаяся к поиску минимального пути в графе, решается методом динамического программирования.
5.3. Функциональное уравнение Беллмана
Назовём состоянием системы вектор координат:S = (ξ1,ξ2 ,...,ξL ). В не-
которых задачах состояние - одна величина. Тогда работу системы можно представить как движение в фазовом пространстве- пространстве состояний. Назовёмшаговым управлением - управление наi-мшаге. Рассмотрим процесс управления системой заm шагов. Функцияωi (S,Ui ) называетсявыиг-
рышем на i-м шаге. ЗдесьS-состояниепередi-мшагом, аUi - управление наi-мшаге.
Величина ωi (S,U i ) должна быть известна до начала динамического про-
граммирования. Если состояние перед i-мшагом былоS и мы приняли какоето управлениеUi, то система перейдёт в новое состояниеS′ =ϕi (S,Ui ). Эта
функция должна быть так же известна. Если эти функции не заданы, то их надо сформулировать. Введём функцию Wi(S)- условный оптимальный выигрыш. Это выигрыш на всех этапах отi до конца, еслиi-йшаг начинается с состоянияS.
Рассмотрим m шагов. Пусть с (i+1)-гошага мы системой управляем оптимально, тогда величина выигрыша будет такая- Wi+1 (S′). Применим наi-м
82
studfiles.net
Исследование операций и методы оптимизации

N2 . Тогда для задачи минимизациидля заданного ε в точке x необходимоопределитьвеличинуизусловия
| , |
где | , g0(X)-–градиентF(X). |
| Более подробно алгоритм решение и примеры можно найти в [7, 16]. |
6.10. Метод проекции градиента
На каждой итерации этого метода предусмотрена процедура возврата очередного приближения градиентного спуска
на допустимое множество U , если. Такой возврат производится
посредством проектирования наU, т.е. заменына ближай-
шую точку множества U.
Определение. Пусть заданы замкнутое множество и точка
. Точканазываетсяпроекцией точки z на множествоU, если
где– расстояние междуточкамиx иy впространствеEn . Очевидно, для точкипроекциясовпадает с z.
Таким образом, в методе проекции градиента последовательные приближения x(k) к точке минимумаX* целевой функцииf(x) на множествеU вычисляются по формулам
, . (6.20)
Рис. 43
118
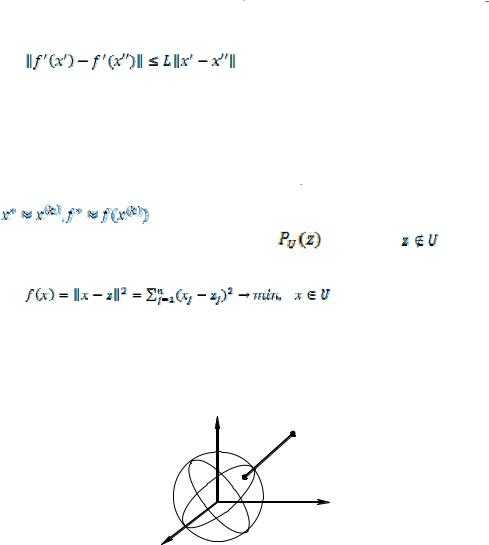
В зависимости от способа вычисления ak из (6.20) различают несколько вариантов метода проекции градиента, самыми распространенными из которых являются следующие.
1) ak находится, как в методе наискорейшего спуска безусловной минимизации, т.е., гдеВ
предположении, что градиент f ′(k) целевой функции удовлетворяет на множествеU условию Липшица, т.е.
(6.21)
для всех , полагаютгдеα - произвольное
число из интервала (0;2/L). Если известна минимальная константа ЛипшицаL из (6.21), то выбирают, как правило,α=1/L.
Вычисления по формуле (6.20) завершаются при выполнении одного из неравенств или, где величинаоп-
ределяет | точность | решения | задачи. | Окончательно | полагают |
|
| . |
|
|
|
Отметим, что определение проекции | для точки | является | |||
самостоятельной задачей нелинейного программирования: |
| ||||
|
|
|
| , | (6.22) |
решение которой может вызвать затруднения.
В частном случае, когда множество U определяется лишь линейными ограничениями, задача (6.22) представляет собой задачу квадратичного программирования. Ее решение может быть найдено за конечное число шагов, как описано выше.
PU(Z)
X1
X2
Рис. 44
Особый интерес при использовании метода проекции градиента представляют такие множества U, для которых задача проектирования (6.22) решается в явном виде.(U - шар, параллелепипед и т.д.)
119
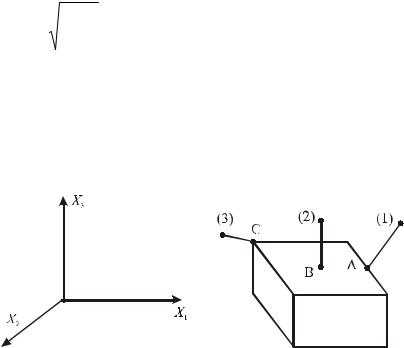
Иногда, как в примере с шаром, нахождение кратчайшего расстояния приводит к задаче на условный экстремум
Ф(X,λ)= ∑n (Xj − Zj )2 +λ∑n (Xj |
| − R0 )2 ; | ∂Ф | = 0; | ∂Ф | = 0 | |||||||||
|
|
| |||||||||||||
|
| j=1 |
|
|
|
|
| j=1 |
|
| ∂Xj | ∂λj | |||
В случае с шаром: |
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| n |
|
|
| (Z U) |
|
|
|
| ||
|
| Z, ∑Z2j ≤ R02 ; |
|
|
|
| |||||||||
|
|
|
| j=1 |
|
|
|
|
|
|
|
|
| ||
P | (Z )= |
| R0 Z |
|
| n | 2 | 2 | ; (Z U) |
|
|
|
| ||
U |
|
|
|
|
| , | ∑Zj | > R0 |
|
|
|
|
| ||
|
| n |
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
| ∑z2 |
|
| j=1 |
|
|
|
|
|
|
|
| |
|
|
| j=1 |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Если область допустимых решений U - параллелепипед, то проекция точки определяется очень просто. Пусть областьU определяется условиями:a1<x1<b1
a2<x2<b2
a3<x3<b3
Рис. 45
Если только одна из координат X j [aj ,bj ] , а остальные нет, то проекцией на параллелепипед будет точка на ребре (т.А).
Если две из координат X j принадлежат областиX j [aj ,bj ] ,
Xk [ak ,bk ] , то проекцией на параллелепипед будет точка на грани (т. В).
Если все три координаты X1 [a1,b1 ], X2 [a2 ,b2 ], X3 [a3 ,b3 ], то проекцией на параллелепипед будет точка в вершине (т.С).
120
6.11. Методы штрафных и барьерных функций
Идея методов штрафных ибарьерных функций заключается в том, что исходная задача НЛП с ограничениями заменяется последовательностьюзадач безусловной оптимизации (т.е. без ограничений) за счет введения новой функции, учитывающей невыполнение ограничений в виде «штрафа»:
С(X)=F(X)+ P(X),
Где F(X) – целевая функция,P(X) – функция, равная в идеалеF(X) в области допустимых решенийU и равная бесконечности вне этой области. Практически вместоP(X) подбирается последовательность функцийPK(X), зависящих отк, так, чтобыlim PK(X)=P(X), прикÆ∞.
На рис.a) иb) показано решение задачиF(x)Æ min, a<x<b.
В методах штрафных функций последовательность точек стремится к решению в допустимой области извне и функции штрафа изменяются вне областиU, поэтому они называют методами свнешней точкой (см. рис.a). В методахбарьерных функций функцияP(X) аппроксимируется барьерными функциями изнутри области (для них ограничения являются барьером), поэтому эти методы называются методами свнутренней точкой.(см. рис.b).
Рассмотрим метод штрафных функций для задачи НЛП
F(X) Æ min, XєU. Заменим эту задачу последовательностью задач безусловной оптимизации
Ck(X)=F(X) + Pk(X)Æ min, k=1,2,3,…, | (6.23) |
Где Pk(X) – функции, которые с ростомk во все большей степени учитывают ограничения, определяемые допустимым множествомU исходной задачи. В методе штрафных функций функцииPk(X) подбираются так, чтобы при большихk функцияСk(X) мало отличалась отF(X) приX U и быстро возрастала при удалении точки от допустимого множестваU. Последовательностью штрафных функций множестваU называется последовательность функций{Pk(X)}, обладающих свойством
a)b)
Рис. 46
121
0, еслиX U, lim Pk (X ) = +∞, еслиХ U.
Рассмотрим один из вариантов метода штрафных функций приближен-
ного решения задачи нелинейного программирования |
|
F(X) Æ min | (6.24) |
gi (X )= 0,i =1,...,l
gi (X )≤ 0,i = l +1,...,m
считая, что функции F(X),gi(X),i=1,…,m , заданы во всем пространствеEn.
Положим |
|
|
Pk(X)= kp(X), k=1,2,3,… | (6.25) | |
где |
|
|
p(X)= Σ gi2(x)+ Σ [gi+(x)]2, |
| |
i=1 i=l+1 |
|
|
0, | gi (X )≤ 0, |
|
gi* (X) = |
|
|
gi(X ), еслиgi (X ) > 0. |
| |
если
Равенство (6.25) определяет последовательность штрафных функций допустимого множества исходной задачи (проверьте!).
При определенных условиях последовательность решений задач безусловной минимизации (6.23), (6.25) сходится к решению x* задачи (6.24), поэтому для достаточно большихk полагаютx*=x(k), F*=F(X(k)).
Критерием достижения требуемой точности решения задачи (6.24) может служить неравенство
||X(k)-X(k/2)||≤ε,
где ε>0 – число, характеризующее точность, k – четное число.
Если в задаче (6.24) F(X) – выпуклая квадратичная функция, аgi(X), i=1, … ,m, - линейные функции, то точное решение вспомогательной задачи (6.23) можно найти из системы линейных уравненийdF(X)/dXj=0, j=1, … , n, определяющих стационарную точку функцииFk(X).
Пример.
Минимизировать −x1x2 при ограничениях
122
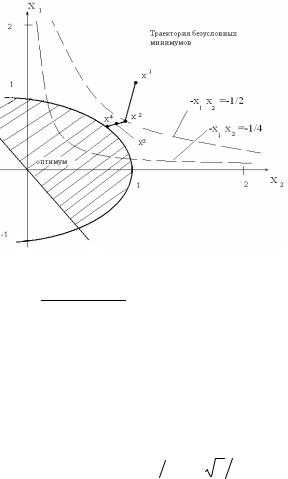
g1 ≡ +x1 +x22 −1 ≤0, g2 ≡ −x1 −x2 ≤0.
В качестве штрафной функции применим следующее
pi(gi) = [(gi+ |
| gi |
| ) / 2]2 , | p(X) = ∑pi [gi (x)] и Pk(X)=k p(X). |
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (+x +x2 −1 + | + x +x2 −1 | ) | 2 |
| (−x | − x |
| + |
| − x | − x |
|
| ) | 2 | ||||||
|
|
|
|
| 1 | 2 |
| 1 | 2 |
|
|
|
|
|
|
|
| ||||||||
Ck (X) = −x1 x2 | + k |
|
|
|
|
|
|
|
| + k | 1 |
| 2 |
|
| 1 |
| 2 |
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
| 2 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
будет функцией, минимизируемой методом внешней точки.
Рис. 47
Значение x(k) для примера
Таблица 39
| k | x1 (k) | x2 (k) |
k1 | 1,0 | 0,89 | 0,64 |
k2 | 2,0 | 0,77 | 0,62 |
k3 | 3,0 | 0,73 | 0,61 |
k4 | 10,0 | 0,67 | 0,58 |
оптимум |
| 2 3 | 3 3 |
|
|
|
|
123
В таблице приведены значения x(k) для четырёх различных значенийk.
Из рисунка видно, что при возрастании k они приближаются к оптимуму из недопустимой области.
Методы внутренней и внешней точки существенно отличаются друг от друга, и не только тем, что в одном из них движение происходит в допустимой области, а в другом - в недопустимой.
Метод барьерных функций.
В методе барьерных функций исходная задача НЛП также сводится к последовательности задач безусловной минимизации (6.23), но функции Pk(X) выбираются таким образом, чтобы при большихk функцииCk(X) из (6.23) мало отличались отF(X) во внутренних точкахx допустимого множестваU. В то же время при приближении точкиX U к границе множестваU эти функции должны неограниченно возрастать.
Определение. Пусть множествоU εn задано. Последовательность функций{Pk (X )}, определенных во всех внутренних точках множестваU,
называется последовательностью барьерных функций этого множества, если выполняются условия:
1. limk→∞ Pk (X )= 0 для любой фиксированной внутренней точкиx множества U.
2. limr→∞ Pk (X (r ) ) = +∞ для любой последовательности{X (r) }внутрен-
них точек множества U, сходящейся к какой либо граничной точке этого множества.
Рассмотрим некоторые варианты метода барьерных функций решения следующей задачи нелинейного программирования:
F(X) Æ min
Отформ
ширине, 14,2 пт,
нумеров 1 + Стил
3, … + Н
Выравни
Выровня
Табуляц Отступ: Поз.табу по левом
gi (X )≤ 0,i =1...,m. | (6.26) | ||||||
Положим |
|
|
|
|
|
| |
P (X) = | 1 | p(X), k=1, 2…, | (6.27) | ||||
| |||||||
k | k |
|
|
|
|
|
|
|
|
|
|
|
|
| |
где |
|
|
|
|
|
|
|
p(X) = ∑im=1 |
| gi(x) |
| −k , k >0 | (6.28) | ||
|
| ||||||
или |
|
|
|
|
|
|
|
124 |
|
|
|
|
|
|
|
p(X )= −∑im=1ln[− gi( x) ] | (6.29) |
Выражения (6.27) – (6.29) определяют последовательности барьерных функций допустимого множества U задачи (6.26) (проверяйте!).
Пусть X(k) – решение задачи безусловной минимизации (6.23), где функцияPk(X) определена равенствами (6.27), (6.28) или (6.29). Полагая
X *≈ X (k ) ,F* ≈ F(X (k ) ) для достаточно большогоk, находим приближен-
ное решение задачи нелинейного программирования (6.24) методом барьерных функций. Для контроля достигнутой точности решения можно использовать критерий (6.4).
Пример. МинимизироватьX1 + X 2 при ограничениях
g1 = +X12 −X 2 ≤0,
g2 = −X1 ≤0 .
В качестве функции p(gi) возьмём логарифмическую функцию. Обозна-
m
чим 1/k=r. Тогда Pr(X))=rp(X), p(X)= −∑ln(−gi (X)) .
n=1
C(X,r) = X1 + X2 −rln(−X12 + X2 ) −rln X1 .
Этот простой пример можно решать аналитически, учитывая, что С(X, r) дважды дифференцируема. Необходимые условия первого порядка принимают вид:
1 + |
| r(2X1 ) |
| − |
| r |
| = 0 , |
|
|
| |||
− X12 +X | 2 | X | 1 |
|
|
| ||||||||
|
|
|
|
|
|
|
| |||||||
1 − |
|
| r |
| = 0 . |
|
|
|
|
|
|
|
| |
| − X 12 +X 2 |
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
| |||
Решая эту систему, получаем |
|
| ||||||||||||
X1 (r)= | −1±1+8r | . |
|
|
|
|
|
| ||||||
|
|
|
|
|
|
| ||||||||
|
| 4 |
|
|
|
|
|
|
|
|
|
| ||
Поскольку значение X1 (r) | должно быть положительно, будем рассмат- | |||||||||||||
ривать лишь один корень | X1 (r)= | −1 | + 1+8r . Тогда | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
| 4 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 125 |

X 2 (r) = | (−1+ 1+ 8r )2 | + r . | |
16 | |||
|
|
Эти значения X1(r) иX2(r) удовлетворяют достаточным условиям и поэтому дают локальный минимум задачи.
Втаблице приведены вычисленные значения X(r) для четырёх различных
r. Этот пример изображён на рисунке. В пределе при rk→0 минимизирующие точки приближаются к решению (0,0).
Значения r иx(r) из примера
Таблица 40
| r | X1 (r) | X 2 (r) |
r1 | 1,000 | 0,500 | 1,250 |
r2 | 0,500 | 0,309 | 0,595 |
r3 | 0,250 | 0,183 | 0,283 |
r4 | 0,100 | 0,085 | 0,107 |
В этой задаче при каждом значении r существует только один локальный минимум. Это происходит так потому, что исходная задача имела единственное решение. Оказывается, что в задачах со многими локальными минимумами (при выполнении вышеупомянутого условия регулярности Слейтера) существует последовательность безусловных локальных минимумов, сходящаяся к каждому из условных локальных минимумов [24,1,12,22].
Рис. 48
126
На рисунке показан пример решения задачи с помощью безусловной логарифмической функции. Допустимая область заштрихована.
6.12. Метод скользящего допуска
Метод скользящего допуска применяется при общей постановке задачи нелинейного программирования:
Минимизировать F(X ),Х Еn при ограничениях
hi (X )= 0 | i =1,....,m |
gi (X )≥ 0 | i = m +1,...,p |
Где функции F(X ),hi (X ), gi (X ) могут быть как линейные, так и не-
линейные. Алгоритм скользящего допуска позволяет улучшить значения целевой функции как за счет информации, получаемой в допустимых точках пространства решения, так и за счет информации, которую удается получить при прохождения через точки, лежащие вне допустимой области, но близкие к допустимым. Интервалы, в пределах которых точки можно считать почти допустимыми, в ходе поиска постепенно сокращаются, так что в пределе (по мере приближения к искомому решению) учитываются только допустимые
точки {Х}.
В качестве метода получения последовательности точек, улучшающих значение целевой функции, используется метод Нелдера-Мида(см. п.6.4). При такой стратегии задачу можно заменить более простой, но имеющей то
же самое решение задачей минимизации F(X ),Х Еn при ограничениях
Ф(к) −Т(Х)≥ 0,
где Ф(к) - значениекритерия скользящего допуска нак-мэтапе;
Т(Х) - мера степени нарушения ограничений рассматриваемой задачи.
Вкачестве Ф выбирают положительно определенную убывающую функцию координат вершин деформируемого многогранника Нелдера и Мида.
Функция Ф служит критерием допуска для нарушения ограничений задачи и прекращения процедуры оптимизации.
Варианты выбора Ф многочисленны.
Например:
127
studfiles.net