Градиентные методы минимизации функций многих переменных. Градиентные методы использующие одномерную оптимизацию носят название метод
3.3. Градиентные методы
В предыдущем разделе рассматривались методы, позволяющие получить решение задачи на основе использования только значений целевой функции. Важность прямых методов несомненна, поскольку в ряде практических инженерных задач информация о значениях целевой функции является единственной надежной информацией, которой располагает исследователь.
f(x) = 2x + 4xx
+ 4xx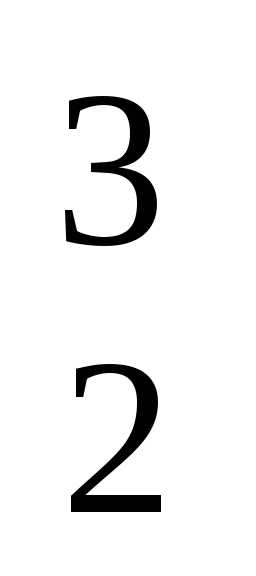 – 10xx
– 10xx + x
+ x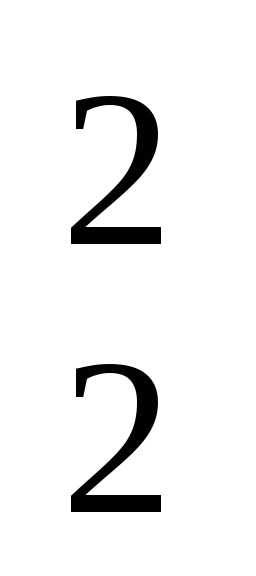
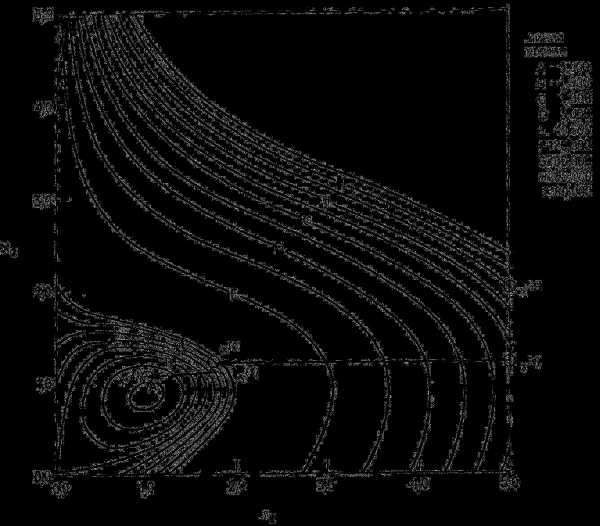
Рис. 3.13. Решение задачи из примера 3.6 по методу сопряженных направлений Пауэлла.
С другой стороны, при использовании даже самых эффективных прямых методов для получения решения иногда требуется чрезвычайно большое количество вычислений значений функции. Это обстоятельство наряду с совершенно естественным стремлением реализовать возможности нахождения стационарных точек [т. е. точек, удовлетворяющих необходимому условию первого порядка (3.15а)] приводит к необходимости рассмотрения методов, основанных на использовании градиента целевой функции. Указанные методы носят итеративный характер так как компоненты градиента оказываются нелинейными функциями управляемых переменных.
Далее везде предполагается, что f(х),  f(x) и
f(x) и 
x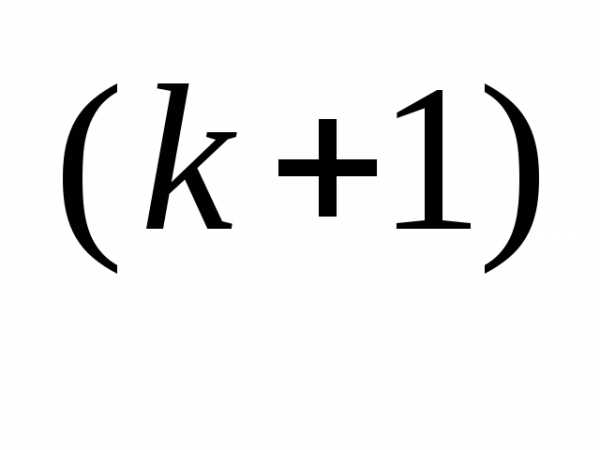 = x
= x +α
+α s(x
s(x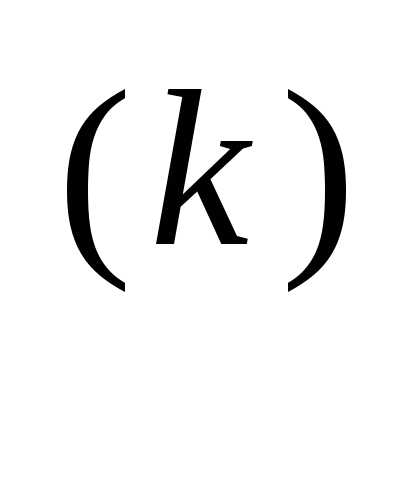
где x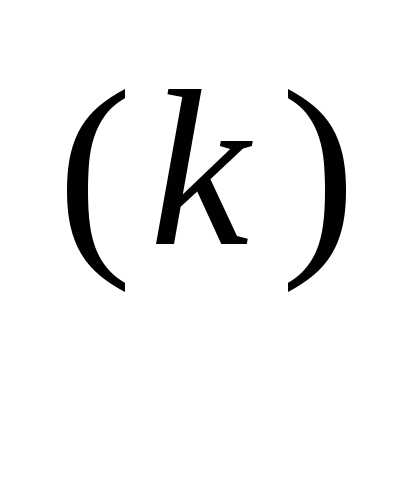 — текущее приближение к решению х*; α
— текущее приближение к решению х*; α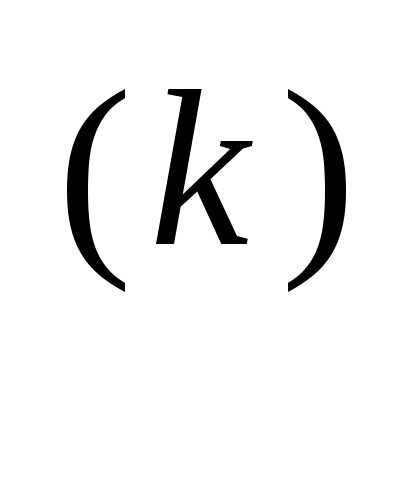 — параметр характеризующий длину шага; s(x
— параметр характеризующий длину шага; s(x ) = s
) = s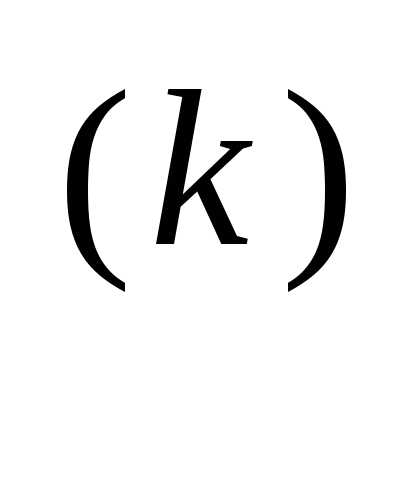 — направление поиска в N-мерном пространстве управляемых переменных xi, i = 1, 2, 3,..., N. Способ определения s(x) и α на каждой итерации связан с особенностями применяемого метода. Обычно выбор α
— направление поиска в N-мерном пространстве управляемых переменных xi, i = 1, 2, 3,..., N. Способ определения s(x) и α на каждой итерации связан с особенностями применяемого метода. Обычно выбор α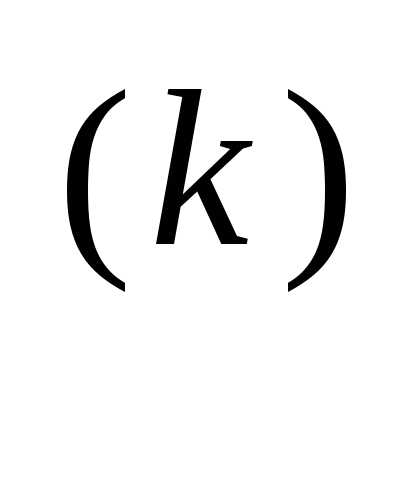 осуществляется путем решения задачи минимизации f(x) в направлении s(x
осуществляется путем решения задачи минимизации f(x) в направлении s(x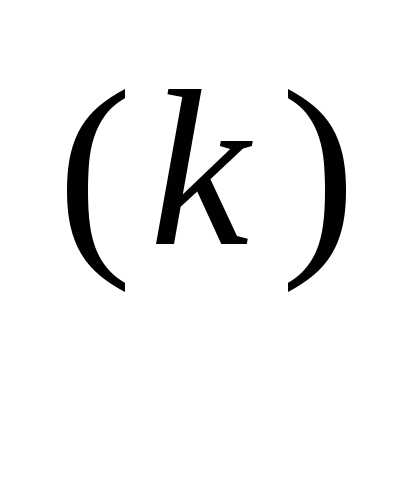 ). Поэтому при реализации изучаемых методов необходимо использовать эффективные алгоритмы одномерной минимизации.
). Поэтому при реализации изучаемых методов необходимо использовать эффективные алгоритмы одномерной минимизации.
3.3.1. Метод Коши [20]
Предположим, что в некоторой точке 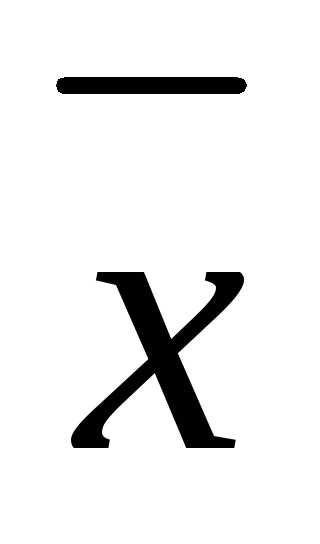 пространства управляемых переменных требуется определить направление наискорейшего локального спуска, т. е. наибольшего локального уменьшения целевой функции. Как и ранее, разложим целевую функцию в окрестности точки
пространства управляемых переменных требуется определить направление наискорейшего локального спуска, т. е. наибольшего локального уменьшения целевой функции. Как и ранее, разложим целевую функцию в окрестности точки  в ряд Тейлора
в ряд Тейлора
f(x) = f (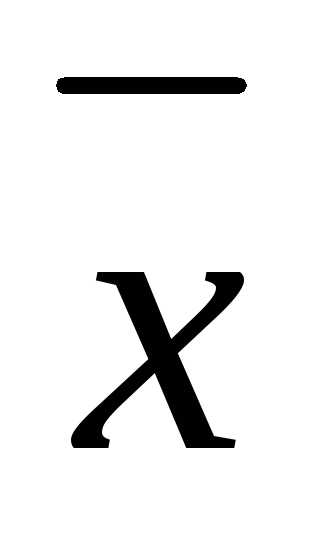 )+
)+ f(
f(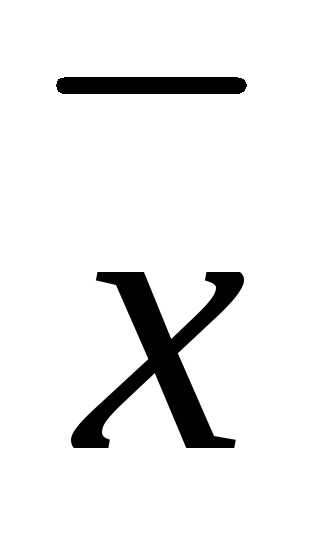 )
) ∆x+… (3.43)
∆x+… (3.43)
и отбросим члены второго порядка и выше. Нетрудно видеть, что локальное уменьшение целевой функции определяется вторым слагаемым, так как значение f (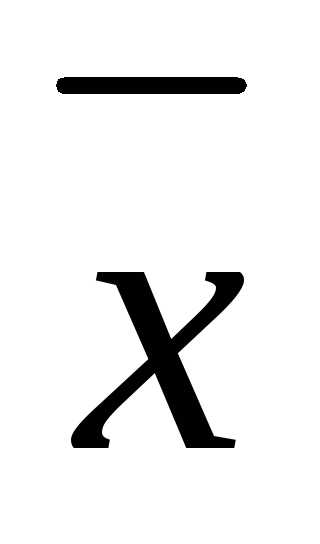
s (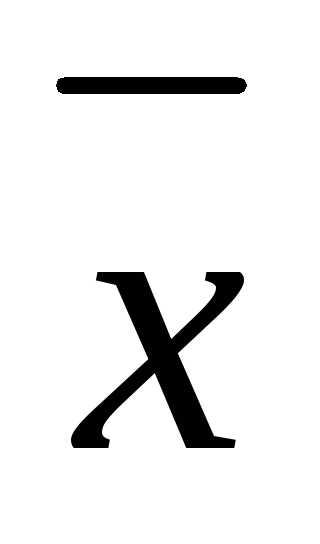 ) = –
) = –  f(
f(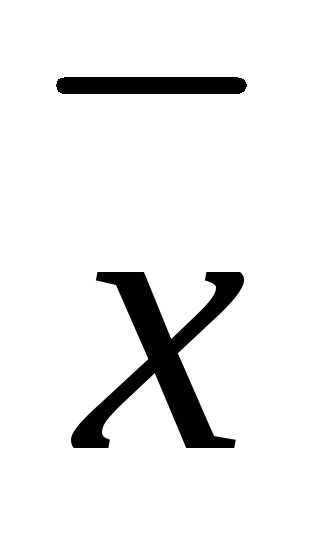 ), (3.44)
), (3.44)
и второе слагаемое примет вид
–α f(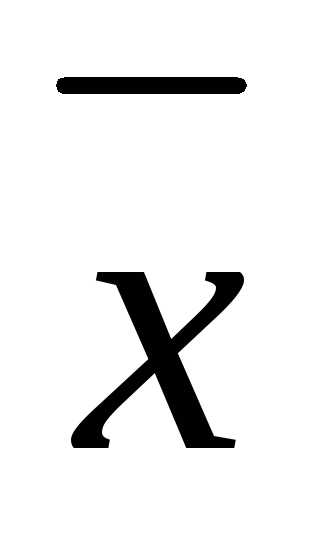 )
)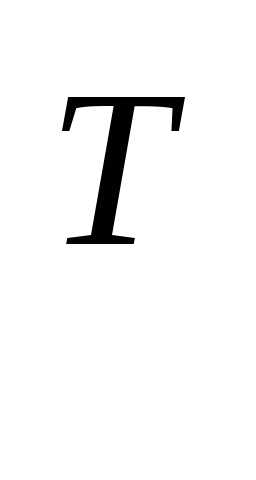
 f(
f(
Рассмотренный случай соответствует наискорейшему локальному спуску. Поэтому в основе простейшего градиентного метода лежит формула
x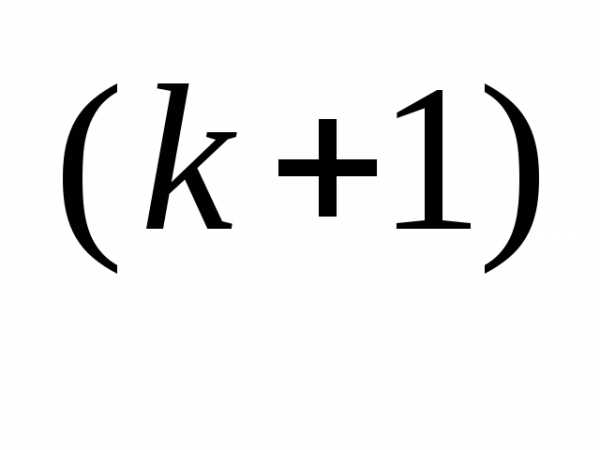 = x
= x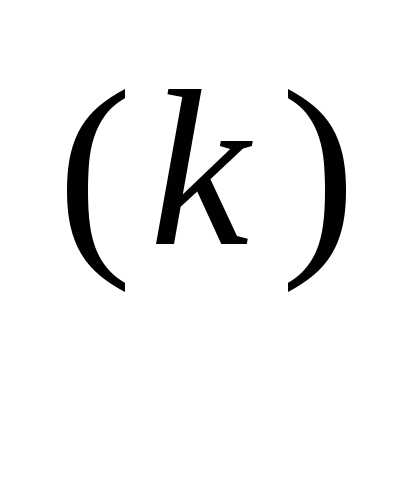 – α
– α  f (x
f (x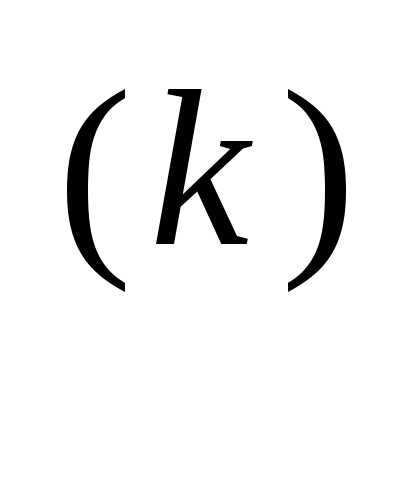 ), (3.45)
), (3.45)
где α — заданный положительный параметр. Метод обладает двумя недостатками: во-первых, возникает необходимость выбора подходящего значения α, и, во-вторых, методу свойственна медленная сходимость к точке минимума вследствие малости f в окрестности этой точки.
Таким образом, целесообразно определять значение α на каждой итерации
x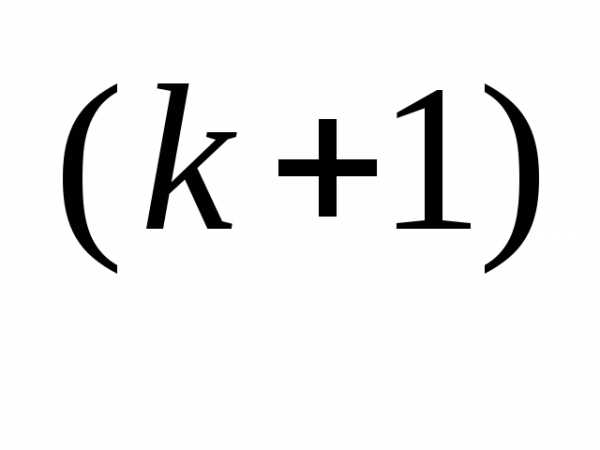
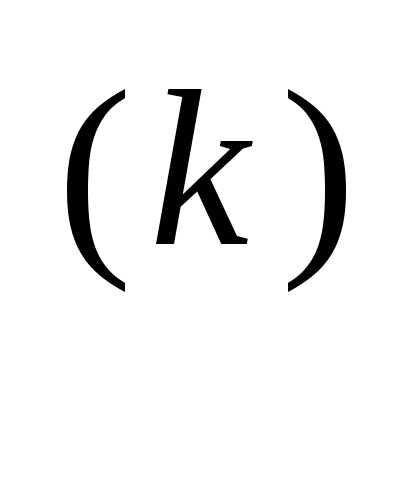 – α
– α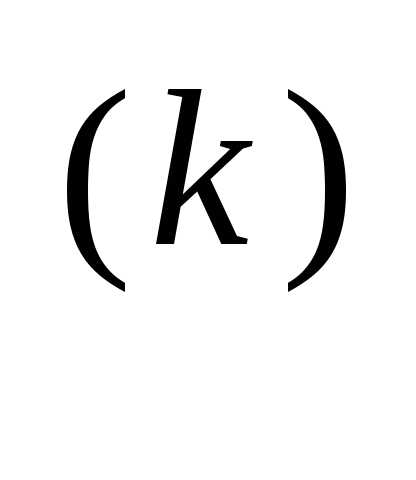
 f (x
f (x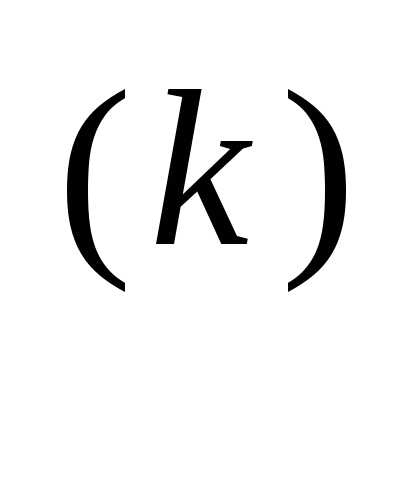 ), (3.46)
), (3.46) Значение α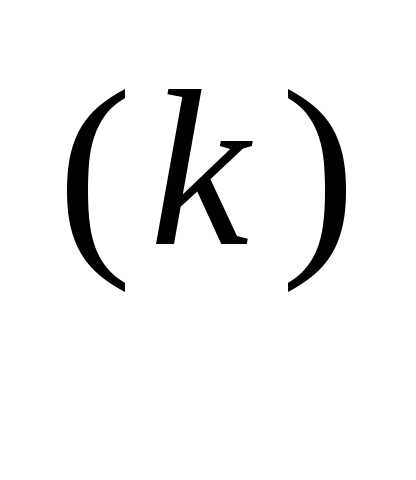 вычисляется путем решения задачи минимизации f (x(k+1)) вдоль направления
вычисляется путем решения задачи минимизации f (x(k+1)) вдоль направления  f (x
f (x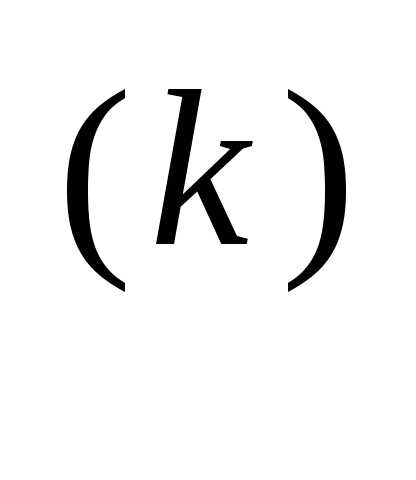 ) с помощью того или иного метода одномерного поиска. Рассматриваемый градиентный метод носит название метода наискорейшего спуска, или метода Коши, поскольку Коши первым использовал аналогичный алгоритм для решения систем линейных уравнений.
) с помощью того или иного метода одномерного поиска. Рассматриваемый градиентный метод носит название метода наискорейшего спуска, или метода Коши, поскольку Коши первым использовал аналогичный алгоритм для решения систем линейных уравнений.
Поиск вдоль прямой в соответствии с формулой (3.46) обеспечивает более высокую надежность метода Коши по сравнению с простейшим градиентным методом, однако скорость его сходимости при решении ряда практических задач остается недопустимо низкой. Это вполне объяснимо, поскольку изменения переменных непосредственно зависят от величины градиента, которая стремится к нулю в окрестности точки минимума, и отсутствует механизм ускорения движения к точке минимума на последних итерациях. Одно из главных преимуществ метода Коши связано с его устойчивостью. Метод обладает важным свойством, которое заключается в том, что при достаточно малой длине шага итерации обеспечивают выполнение неравенства
f (x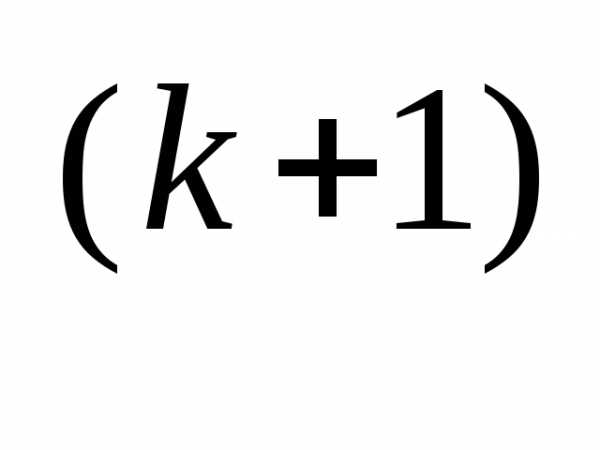 ) ≤ f (x
) ≤ f (x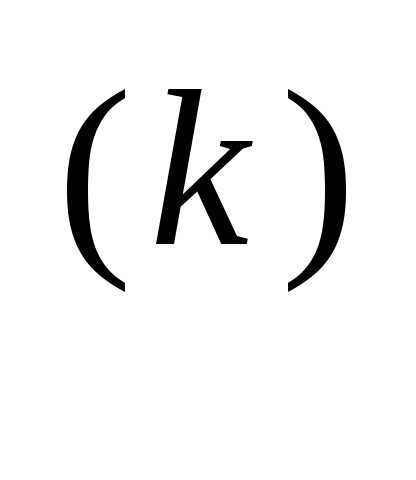 ). (3.47)
). (3.47)
С учетом этого свойства заметим, что метод Коши, как правило, позволяет существенно уменьшить значение целевой функции при движении из точек, расположенных на значительных расстояниях от точки минимума, и поэтому часто используется при реализации градиентных методов в качестве начальной процедуры. Наконец, на примере метода Коши можно продемонстрировать отдельные приемы, которые используются при реализации различных градиентных алгоритмов.
Пример 3.7. Метод Коши
Рассмотрим функцию
f(x) = 8x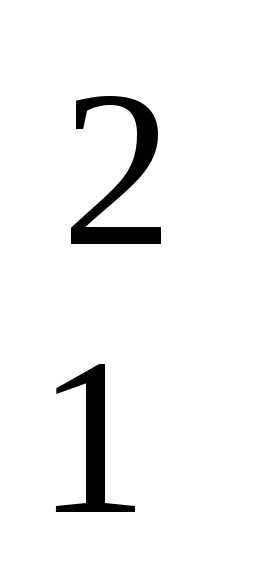 + 4xx
+ 4xx + 5x
+ 5x
и используем метод Коши для решения задачи ее минимизации.
Решение. Прежде всего вычислим компоненты градиента
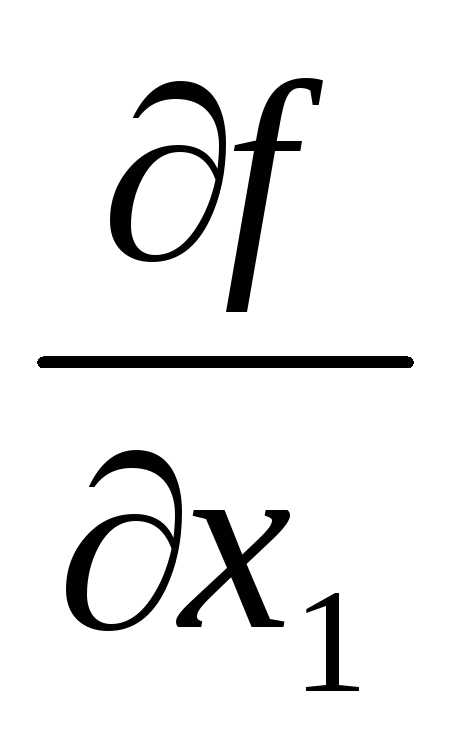 = 16x+ 4x,
= 16x+ 4x, 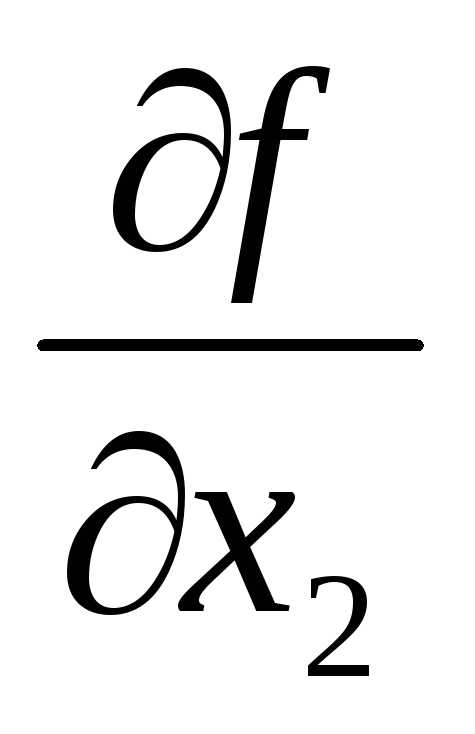 = 10x
= 10x + 4x.
+ 4x.
Для того чтобы применить метод наискорейшего спуска, зададим начальное приближение
x(0) = [10, 10]T
и с помощью формулы (3.46) построим новое приближение
x = x
= x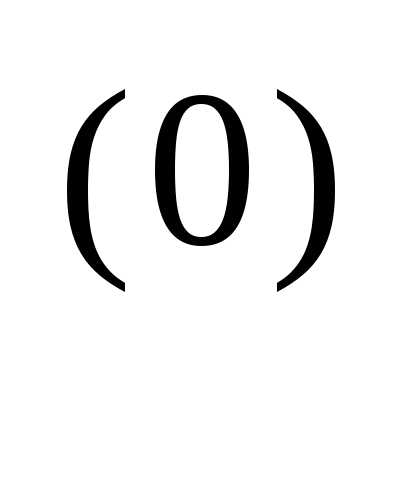 - α
- α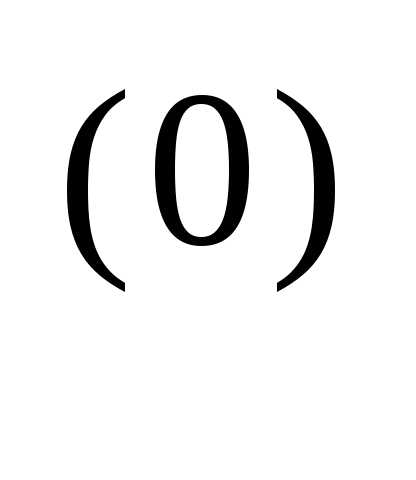
 f (x
f (x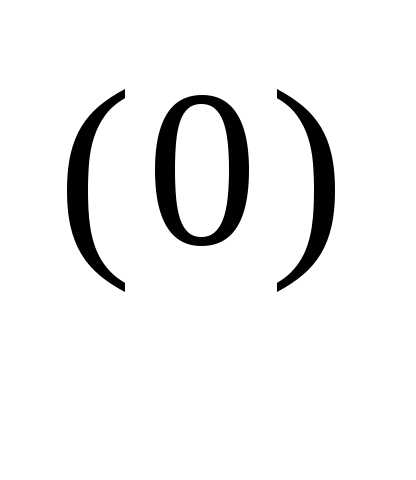 )
)
f (x) = 8x + 4xx
+ 4xx + 5x
+ 5x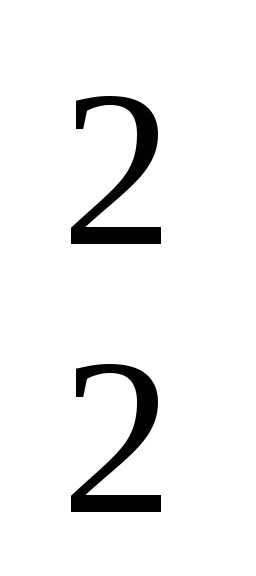
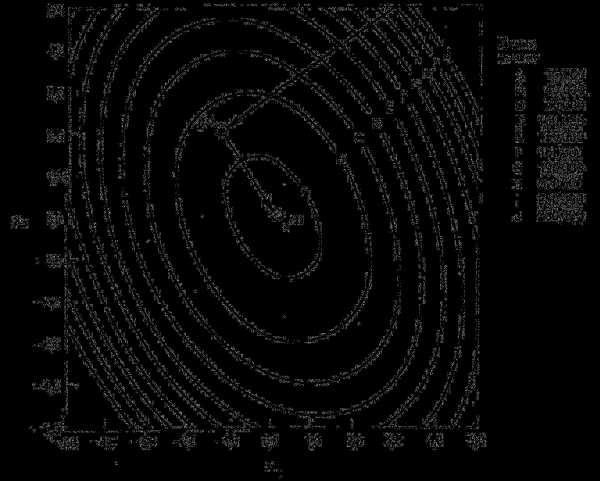
Рис. 3.14. Итерации по методу Коши с использованием метода квадратичной интерполяции.
Таблица 3.1. Результаты вычислений по методу Коши
| k | x | x | f(x |
| 1 | -1.2403 | 2.1181 | 24.2300 |
| 2 | 0.1441 | 0.1447 | 0.3540 |
| 3 | -0.0181 | 0.0309 | 0.0052 |
| 4 | 0.0021 | 0.0021 | 0.0000 |
Выберем α таким образом, чтобы f (x(1)) → min.; α
таким образом, чтобы f (x(1)) → min.; α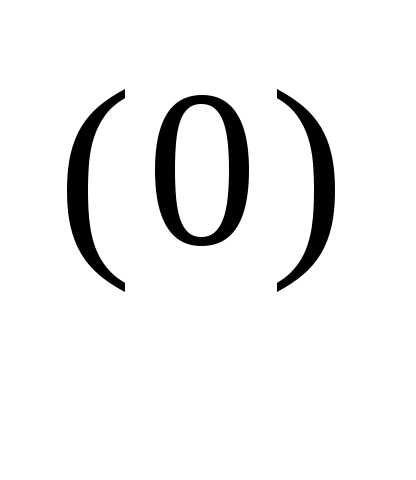 = 0,056. Следовательно, x(1) = [–1,20, 2.16]T Далее найдем точку
= 0,056. Следовательно, x(1) = [–1,20, 2.16]T Далее найдем точку
x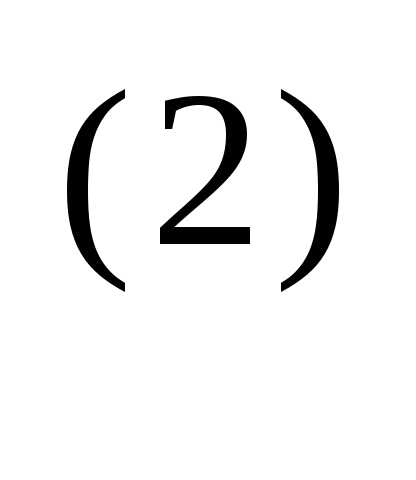 = x
= x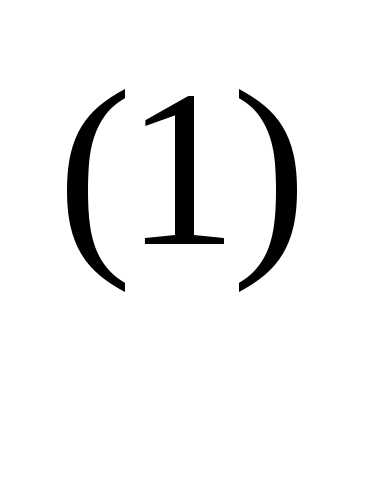 – α
– α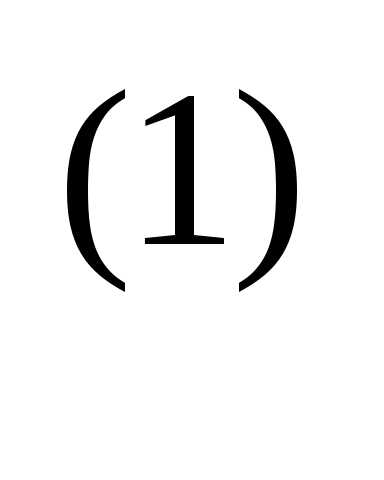 f (x
f (x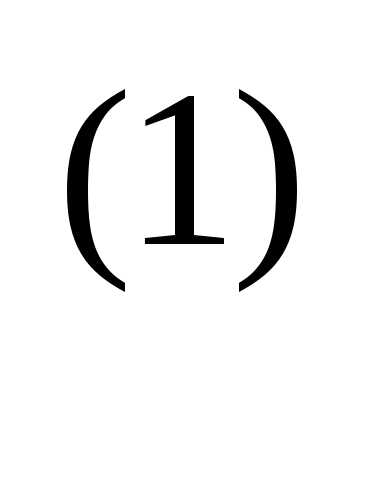 ),
),
вычислив градиент в точке x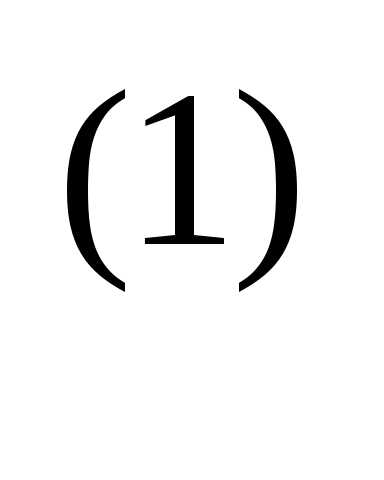 и проведя поиск вдоль прямой.
и проведя поиск вдоль прямой.
В таблице 3.1 представлены данные, полученные при проведении итераций на основе одномерного поиска по методу квадратичной интерполяции [21, 22]. Последовательность полученных точек изображена на рис. 3.14.
Несмотря на то что метод Коши не имеет большого практического значения, он реализует важнейшие шаги большинства градиентных методов. Блок-схема алгоритма Коши приведена на рис. 3.15. Заметим, что работа алгоритма завершается, когда модуль градиента или модуль вектора ∆x становится достаточно малым.
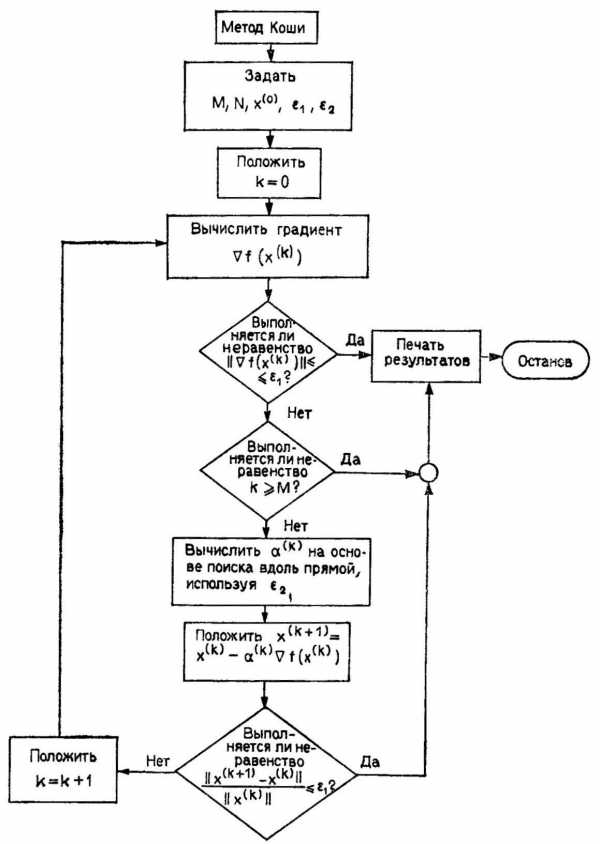
Рис. 3.15. Блок-схема метода Коши.
studfiles.net
Градиентные методы
скачать Градиентные методы Градиентные методы безусловной оптимизации используют только первые производные целевой функции и являются методами линейной аппроксимации на каждом шаге, т.е. целевая функция на каждом шаге заменяется касательной гиперплоскостью к ее графику в текущей точке.На k-м этапе градиентных методов переход из точки Xk в точку Xk+1 описывается соотношением:
Xk+1= Xk+ kSk, (1.2)
где k- величина шага, k- вектор в направлении Xk+1-Xk.
Методы наискорейшего спускаВпервые такой метод рассмотрел и применил еще О. Коши в XVIII в. Идея его проста: градиент целевой функции f(X) в любой точке есть вектор в направлении наибольшего возрастания значения функции. Следовательно, антиградиент будет направлен в сторону наибольшего убывания функции и является направлением наискорейшего спуска. Антиградиент (и градиент) ортогонален поверхности уровня f(X) в точке X. Если в (1.2) ввести направление
,
то это будет направление наискорейшего спуска в точке Xk.
Получаем формулу перехода из Xk в Xk+1:
.
Антиградиент дает только направление спуска, но не величину шага. В общем случае один шаг не дает точку минимума, поэтому процедура спуска должна применяться несколько раз. В точке минимума все компоненты градиента равны нулю.
Все градиентные методы используют изложенную идею и отличаются друг от друга техническими деталями: вычисление производных по аналитической формуле или конечно-разностной аппроксимации; величина шага может быть постоянной, меняться по каким-либо правилам или выбираться после применения методов одномерной оптимизации в направлении антиградиента и т.д. и т.п.
Останавливаться подробно мы не будем, т.к. метод наискорейшего спуска не рекомендуется обычно в качестве серьезной оптимизационной процедуры.
Одним из недостатков этого метода является то, что он сходится к любой стационарной точке, в том числе и седловой, которая не может быть решением.
Но самое главное - очень медленная сходимость наискорейшего спуска в общем случае. Дело в том, что спуск является "наискорейшим" в локальном смысле. Если гиперпространство поиска сильно вытянуто ("овраг"), то антиградиент направлен почти ортогонально дну "оврага", т.е. наилучшему направлению достижения минимума. В этом смысле прямой перевод английского термина "steepest descent", т.е. спуск по наиболее крутому склону более соответствует положению дел, чем термин "наискорейший", принятый в русскоязычной специальной литературе. Одним из выходов в этой ситуации является использование информации даваемой вторыми частными производными. Другой выход - изменение масштабов переменных.
Метод сопряженного градиента Флетчера-РивсаВ методе сопряженного градиента строится последовательность направлений поиска , являющихся линейными комбинациями , текущего направления наискорейшего спуска, и , предыдущих направлений поиска, т.е.
,
причем коэффициенты выбираются так, чтобы сделать направления поиска сопряженными. Доказано, что
и это очень ценный результат, позволяющий строить быстрый и эффективный алгоритм оптимизации.
Алгоритм Флетчера-Ривса.
1. В X0 вычисляется .
2. На k-ом шаге с помощь одномерного поиска в направлении находится минимум f(X), который и определяет точку Xk+1.
3. Вычисляются f(Xk+1) и .
4. Направление определяется из соотношения:
5. После (n+1)-й итерации (т.е. при k=n) производится рестарт: полагается X0=Xn+1 и осуществляется переход к шагу 1.
6. Алгоритм останавливается, когда , где - произвольная константа.
Преимуществом алгоритма Флетчера-Ривса является то, что он не требует обращения матрицы и экономит память ЭВМ, так как ему не нужны матрицы, используемые в Ньютоновских методах, но в то же время почти столь же эффективен как квази-Ньютоновские алгоритмы. Т.к. направления поиска взаимно сопряжены, то квадратичная функция будет минимизирована не более, чем за n шагов. В общем случае используется рестарт, который позволяет получать результат.
Алгоритм Флетчера-Ривса чувствителен к точности одномерного поиска, поэтому при его использовании необходимо устранять любые ошибки округления, которые могут возникнуть. Кроме того, алгоритм может отказать в ситуациях, где Гессиан становится плохо обусловленным. Гарантии сходимости всегда и везде у алгоритма нет, хотя практика показывает, что почти всегда алгоритм дает результат. Ньютоновские методы
Направление поиска, соответствующее наискорейшему спуску, связано с линейной аппроксимацией целевой функции. Методы, использующие вторые производные, возникли из квадратичной аппроксимации целевой функции, т. е. при разложении функции в ряд Тейлора отбрасываются члены третьего и более высоких порядков.
,
где - матрица Гессе.
Минимум правой части (если он существует) достигается там же, где и минимум квадратичной формы. Запишем формулу для определения направления поиска :
.
Минимум достигается при .
Алгоритм оптимизации, в котором направление поиска определяется из этого соотношения, называется методом Ньютона, а направление - ньютоновским направлением.
В задачах поиска минимума произвольной квадратичной функции с положительной матрицей вторых производных метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки.
Классификация Ньютоновских методов
Собственно метод Ньютона состоит в однократном применении Ньютоновского направления для оптимизации квадратичной функции. Если же функция не является квадратичной, то верна следующая теорема.
Теорема 1.4. Если матрица Гессе нелинейной функции f общего вида в точке минимума X* положительно определена, начальная точка выбрана достаточно близко к X* и длины шагов подобраны верно, то метод Ньютона сходится к X* с квадратичной скоростью.
Метод Ньютона считается эталонным, с ним сравнивают все разрабатываемые оптимизационные процедуры. Однако метод Ньютона работоспособен только при положительно определенной и хорошо обусловленной матрицей Гессе (определитель ее должен быть существенно больше нуля, точнее отношение наибольшего и наименьшего собственных чисел должно быть близко к единице). Для устранения этого недостатка используют модифицированные методы Ньютона, использующие ньютоновские направления по мере возможности и уклоняющиеся от них только тогда, когда это необходимо.
Общий принцип модификаций метода Ньютона состоит в следующем: на каждой итерации сначала строится некоторая "связанная" с положительно определенная матрица , а затем вычисляется по формуле . Так как положительно определена, то - обязательно будет направлением спуска. Процедуру построения организуют так, чтобы она совпадала с матрицей Гессе, если она является положительно определенной. Эти процедуры строятся на основе некоторых матричных разложений.
Другая группа методов, практически не уступающих по быстродействию методу Ньютона, основана на аппроксимации матрицы Гессе с помощью конечных разностей, т.к. не обязательно для оптимизации использовать точные значения производных. Эти методы полезны, когда аналитическое вычисление производных затруднительно или просто невозможно. Такие методы называются дискретными методами Ньютона.
Залогом эффективности методов ньютоновского типа является учет информации о кривизне минимизируемой функции, содержащейся в матрице Гессе и позволяющей строить локально точные квадратичные модели целевой функции. Но ведь возможно информацию о кривизне функции собирать и накапливать на основе наблюдения за изменением градиента во время итераций спуска. Соответствующие методы, опирающиеся на возможность аппроксимации кривизны нелинейной функции без явного формирования ее матрицы Гессе, называют квази-Ньютоновскими методами.
Отметим, что при построении оптимизационной процедуры ньютоновского типа (в том числе и квази-Ньютоновской) необходимо учитывать возможность появления седловой точки. В этом случае вектор наилучшего направления поиска будет все время направлен к седловой точке, вместо того, чтобы уходить от нее в направлении "вниз".
Метод Ньютона-РафсонаДанный метод состоит в многократном использовании Ньютоновского направления при оптимизации функций, не являющихся квадратичными.
Основная итерационная формула многомерной оптимизации Xk+1= Xk+ k+1 используется в этом методе при выборе направления оптимизации из соотношения , k+1 = 1.
Реальная длина шага скрыта в ненормализованном Ньютоновском направлении . Так как этот метод не требует значения целевой функции в текущей точке, то его иногда называют непрямым или аналитическим методом оптимизации. Его способность определять минимум квадратичной функции за одно вычисление выглядит на первый взгляд исключительно привлекательно. Однако это "одно вычисление" требует значительных затрат. Прежде всего, необходимо вычислить n частных производных первого порядка и n(n+1)/2 - второго. Кроме того, матрица Гессе должна быть инвертирована. Это требует уже порядка n3 вычислительных операций. С теми же самыми затратами методы сопряженных направлений или методы сопряженного градиента могут сделать порядка n шагов, т.е. достичь практически того же результата. Таким образом, итерация метода Ньютона-Рафсона не дает преимуществ в случае квадратичной функции.
Если же функция не квадратична, то
- начальное направление уже, вообще говоря, не указывает действительную точку минимума, а значит, итерации должны повторяться неоднократно;
- шаг единичной длины может привести в точку с худшим значением целевой функции, а поиск может выдать неправильное направление, если, например, гессиан не является положительно определенным;
- гессиан может стать плохо обусловленным, что сделает невозможным его инвертирование, т.е. определение направления для следующей итерации.
Сама по себе стратегия не различает, к какой именно стационарной точке (минимума, максимума, седловой) приближается поиск, а вычисления значений целевой функции, по которым можно было бы отследить, не возрастает ли функция, не делаются. Значит, все зависит от того, в зоне притяжения какой стационарной точки оказывается стартовая точка поиска. Стратегия Ньютона-Рафсона редко используется сама по себе без модификации того или иного рода. Методы Пирсона
Пирсон предложил несколько методов с аппроксимацией обратного гессиана без явного вычисления вторых производных, т.е. путем наблюдений за изменениями направления антиградиента. При этом получаются сопряженные направления. Эти алгоритмы отличаются только деталями. Приведем те из них, которые получили наиболее широкое распространение в прикладных областях.
Алгоритм Пирсона № 2.
В этом алгоритме обратный гессиан аппроксимируется матрицей Hk, вычисляемой на каждом шаге по формуле
Hk+1 = Hk + .
В качестве начальной матрицы H0 выбирается произвольная положительно определенная симметрическая матрица.
Данный алгоритм Пирсона часто приводит к ситуациям, когда матрица Hk становится плохо обусловленной, а именно - она начинает осцилировать, колеблясь между положительно определенной и не положительно определенной, при этом определитель матрицы близок к нулю. Для избежания этой ситуации необходимо через каждые n шагов перезадавать матрицу, приравнивая ее к H0.
Алгоритм Пирсона № 3.
В этом алгоритме матрица Hk+1 определяется из формулы
Hk+1 = Hk + [Xk+1-Xk-Hk (f(Xk+1)- f(Xk))]
Траектория спуска, порождаемая алгоритмом, аналогична поведению алгоритма Дэвидона-Флетчера-Пауэлла, но шаги немного короче. Пирсон также предложил разновидность этого алгоритма с циклическим перезаданием матрицы.
Проективный алгоритм Ньютона-Рафсона
Пирсон предложил идею алгоритма, в котором матрица рассчитывается из соотношения
Hk+1 = Hk + ,
H0=R0, где матрица R0 такая же как и начальные матрицы в предыдущих алгоритмах.
Когда k кратно числу независимых переменных n, матрица Hk заменяется на матрицу Rk+1, вычисляемую как сумма
Rk +.
Величина Hk(f(Xk+1) - f(Xk)) является проекцией вектора приращения градиента (f(Xk+1)-f(Xk)), ортогональной ко всем векторам приращения градиента на предыдущих шагах. После каждых n шагов Rk является аппроксимацией обратного гессиана H-1(Xk), так что в сущности осуществляется (приближенно) поиск Ньютона. Метод Дэвидона-Флетчера-Пауэла
Этот метод имеет и другие названия - метод переменной метрики, квазиньютоновский метод, т.к. он использует оба эти подхода.
Метод Дэвидона-Флетчера-Пауэла (ДФП) основан на использовании ньютоновских направлений, но не требует вычисления обратного гессиана на каждом шаге. Направление поиска на шаге k является направлением , где Hi- положительно определенная симметричная матрица, которая обновляется на каждом шаге и в пределе становится равной обратному гессиану. В качестве начальной матрицы H обычно выбирают единичную. Итерационная процедура ДФП может быть представлена следующим образом:
1. На шаге k имеются точка Xk и положительно определенная матрица Hk.
2. В качестве нового направления поиска выбирается
3. Одномерным поиском (обычно кубической интерполяцией) вдоль направления определяется k, минимизирующее функцию .
4. Полагается .
5. Полагается .
6. Определяется и . Если Vk или достаточно малы, процедура завершается.
7. Полагается Uk= f(Xk+1) - f(Xk).
8. Матрица Hk обновляется по формуле
9. Увеличить k на единицу и вернуться на шаг 2.
Метод эффективен на практике, если ошибка вычислений градиента невелика и матрица Hk не становится плохо обусловленной.
Матрица Ak обеспечивает сходимость Hk к G-1, матрица Bk обеспечивает положительную определенность Hk+1 на всех этапах и в пределе исключает H0.
В случае квадратичной функции , т.е. алгоритм ДФП использует сопряженные направления.
Таким образом, метод ДФП использует как идеи ньютоновского подхода, так и свойства сопряженных направлений, и при минимизации квадратичной функции сходится не более чем за n итераций. Если оптимизируемая функция имеет вид, близкий к квадратичной функции, то метод ДФП эффективен за счет хорошей аппроксимации G-1(метод Ньютона). Если же целевая функция имеет общий вид, то метод ДФП эффективен за счет использования сопряженных направлений.
На практике оказалось, что метод ДФП может давать отрицательные шаги или окончиться в нестационарной точке. Это возможно, когда Hk+1 становится плохо обусловленной. Этого можно избежать путем увеличения числа получаемых значимых цифр или перезаданием матрицы Hk+1 в виде специальной диагональной матрицы H, где
.
Ошибки округления и особенно неточность линейного поиска может послужить причиной потери устойчивости метода ДФП и даже привести к ошибочным шагам, когда значение целевой функции на некоторой итерации возрастает вместо того, чтобы уменьшаться.
По классификации Ньютоновских методов данный алгоритм является квази-Ньютоновским, хотя он использует в явном виде только первые частные производные, а значит, может рассматриваться и как градиентный метод.
Практическая проверка эффективности алгоритма показала, что он столь же эффективен, как и метод Флетчера-Ривса.
скачатьnenuda.ru
Лекция №11
Лекция №11
Тема: «Градиентные численные методы поиска экстремального значения целевой функции»
План лекции:
Градиентный метод.
Частичный градиентный метод.
Обобщенный градиентный метод.
Двойственный градиентный метод.
Метод Ньютона-Рафсона.
Метод наискорейшего спуска. (Градиентный метод).
Необходимо:
Конспект лекций.
Метод. Руководство по выполнению ДЗ №1.
Руководство по выполнению ДЗ №2.
Руководство по выполнению лабор. работ №1, 2.
Руководство по выполнению лабор. работ № 3,4,5.
Градиентные методы оптимизации
Градиентные методы оптимизации относятся к численным методам поискового типа. Они универсальны, хорошо приспособлены для работы с современными цифровыми вычислительными машинами и в большинстве случаев весьма эффективны при поиске экстремального значения нелинейных функций с ограничениями и без них, а также тогда, когда аналитический вид функции вообще неизвестен. Вследствие этого градиентные, или поисковые, методы широко применяются на практике.
Сущность указанных методов заключается в определении значений независимых переменных, дающих наибольшие изменения целевой функции. Обычно для этого двигаются вдоль градиента, ортогонального к контурной поверхности в данной точке.
Различные поисковые методы в основном отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, критериями окончания поиска, простотой алгоритмизации и применимостью для различных ЭВМ. Техника поиска экстремума основана на расчетах, которые позволяют определить направление наиболее быстрого изменения оптимизируемого критерия.
Если критерий задан уравнением
, (3)
то его градиент в точке (x1, x2,…, xn) определяется вектором:
. (4)
Частная производная пропорциональна косинусу угла, образуемого вектором градиента с i-й осью координат. При этом
(5)
Наряду с определением направления градиентного вектора основным вопросом, решаемым при использовании градиентных методов, является выбор шага движения по градиенту. Величина шага в направлении gradF в значительной степени зависит от вида поверхности. Если шаг слишком мал, потребуются продолжительные расчеты; если слишком велик, можно проскочить оптимум. Размер шага должен удовлетворять условию, при котором все шаги от базисной точки лежат в том же самом направлении, что и градиент в базисной точке. Размеры шага по каждой переменной xi вычисляются из значений частных производных в базовой (начальной) точке:
, (6)
где К – константа, определяющая размеры шага и одинаковая для всех i-х направлений. Только в базовой точке градиент строго ортогонален к поверхности. Если же шаги слишком велики в каждом i-м направлении, вектор из базисной точки не будет ортогонален к поверхности в новой точке.
Если выбор шага был удовлетворительным, производная в следующей точке существенно близка к производной в базисной точке.
Для линейных функций градиентное направление не зависит от положения на поверхности, для которой оно вычисляется. Если поверхность имеет вид
то
и компонента градиента в i-м направлении равна
. (7)
Для нелинейной функции направление градиентного вектора зависит от точки на поверхности, в которой он вычисляется.
Несмотря на существующие различия между градиентными методами, последовательность операций при поиске оптимума в большинстве случаев одинакова и сводится к следующему:
а) выбирается базисная точка;
б) определяется направление движения от базисной точки;
в) находится размер шага;
г) определяется следующая точка поиска;
д) значение целевой функции в данной точке сравнивается с ее значением в предыдущей точке;
е) вновь определяется направление движения и процедура повторяется до достижения оптимального значения.
Обобщенный градиентный спуск
Пусть 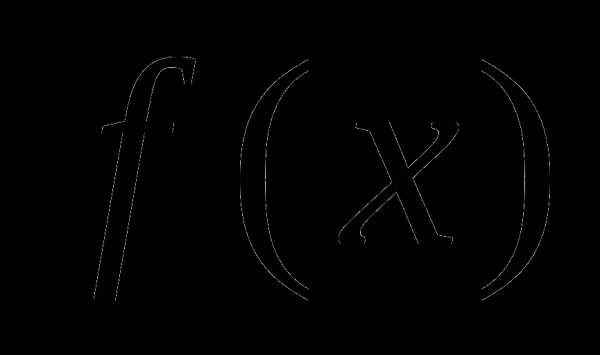 – выпуклая функция, определенная на евклидовом пространстве
– выпуклая функция, определенная на евклидовом пространстве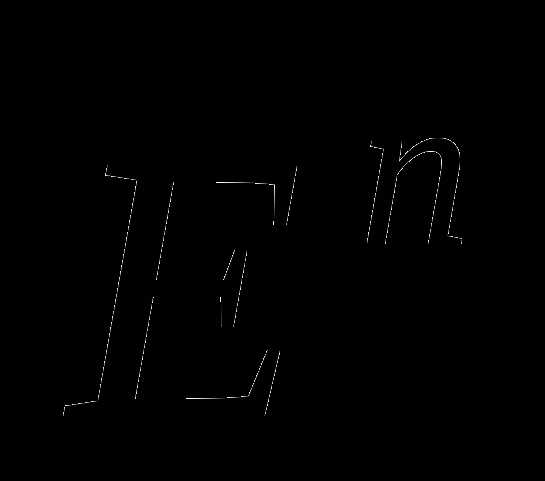 ,
, – множество минимумов (оно может быть и пустым),
– множество минимумов (оно может быть и пустым),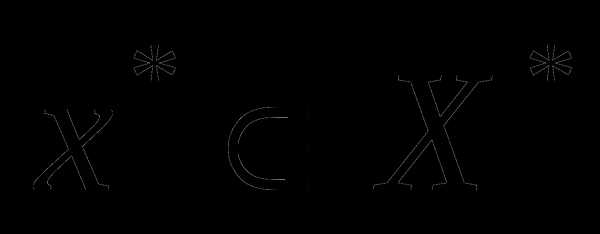 – точка минимума;;
– точка минимума;;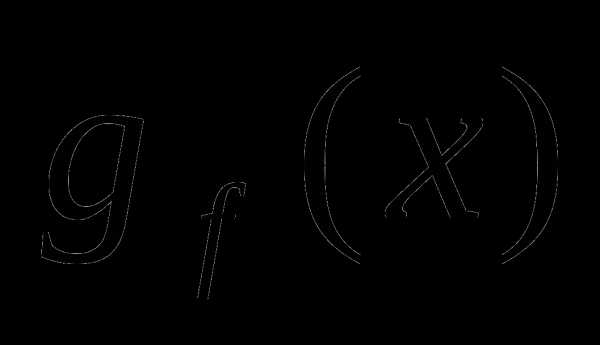 – субградиент функции
– субградиент функции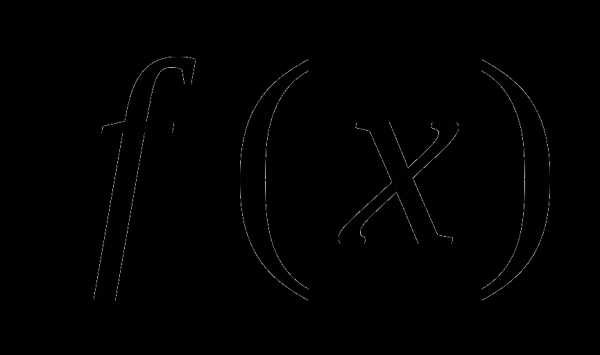 в точке
в точке . Субградиент
. Субградиент 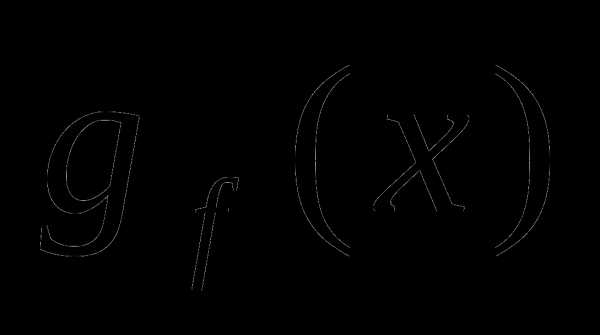 функции
функции в точке
в точке есть вектор
есть вектор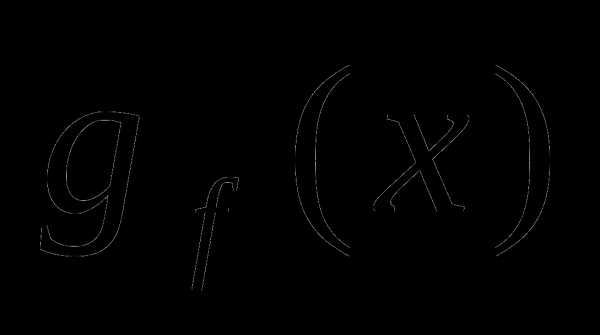 такой, что для всех
такой, что для всех 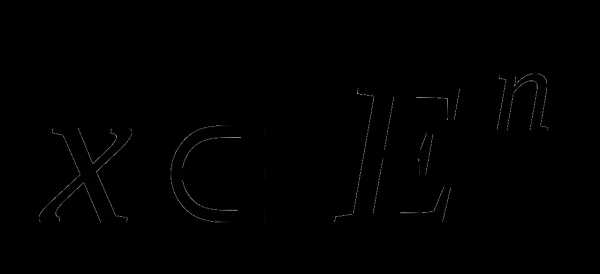 . Из определения субградиента следует, что если , то (1) Геометрически формула (1) означает, что антисубградиент в точке
. Из определения субградиента следует, что если , то (1) Геометрически формула (1) означает, что антисубградиент в точке 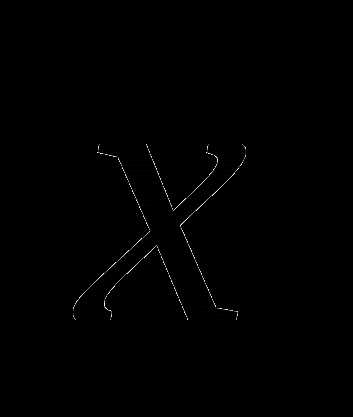 образует острый угол с произвольным направлением, проведенным из
образует острый угол с произвольным направлением, проведенным из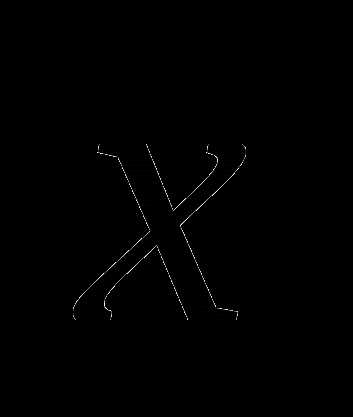 в сторону точки
в сторону точки с меньшим значением
с меньшим значением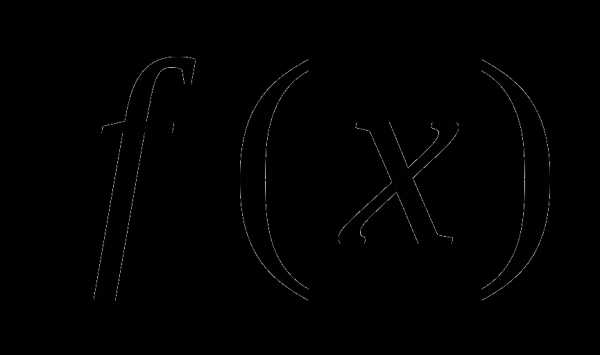 . Отсюда, если
. Отсюда, если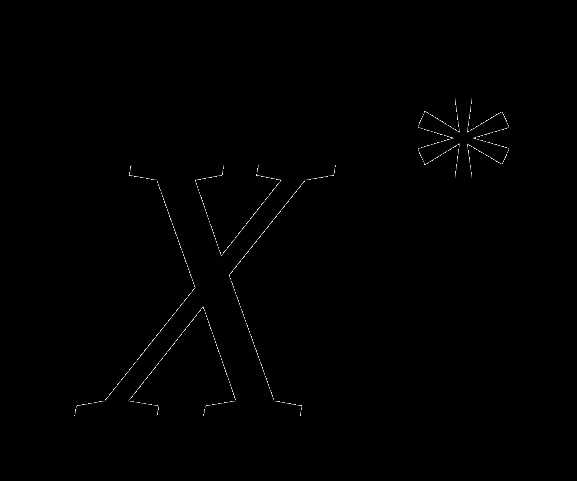 непусто,
непусто, , то при движении из
, то при движении из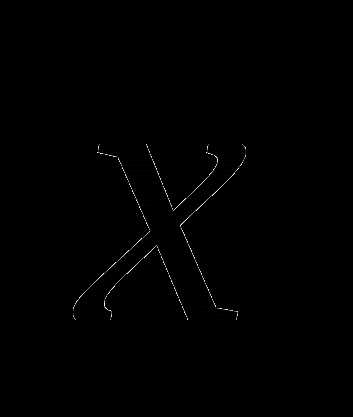 в направлении
в направлении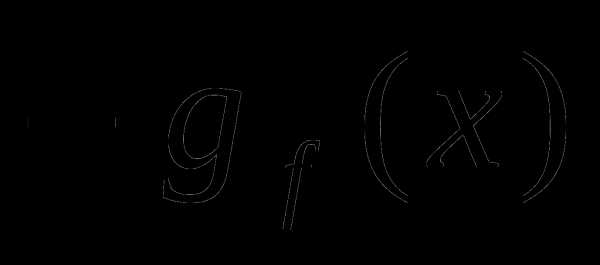
 с достаточно малым шагом расстояние до
с достаточно малым шагом расстояние до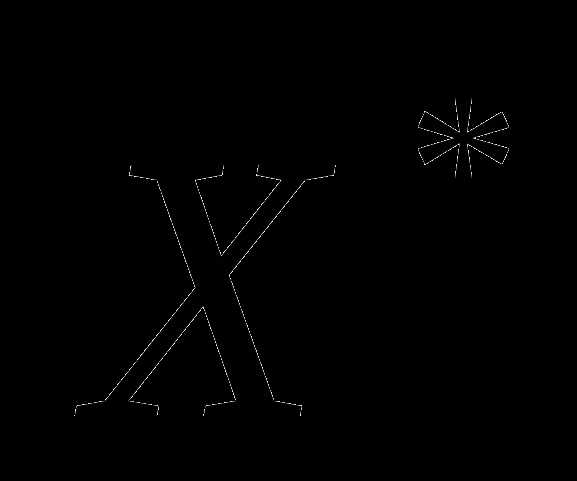 убывает. Этот простой факт лежит в основе субградиентного метода или метода обобщенного градиентного спуска (ОГС), впервые предложенного в [1] в связи с решением сетевой транспортной задачи. Методом обобщенного градиентного спуска (ОГС) называется процедура построения минимизирующей последовательности
убывает. Этот простой факт лежит в основе субградиентного метода или метода обобщенного градиентного спуска (ОГС), впервые предложенного в [1] в связи с решением сетевой транспортной задачи. Методом обобщенного градиентного спуска (ОГС) называется процедура построения минимизирующей последовательности 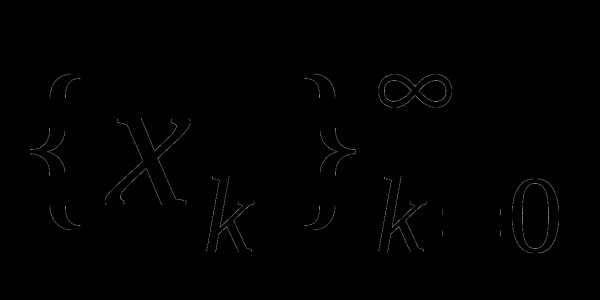 , где
, где – начальное приближение, а
– начальное приближение, а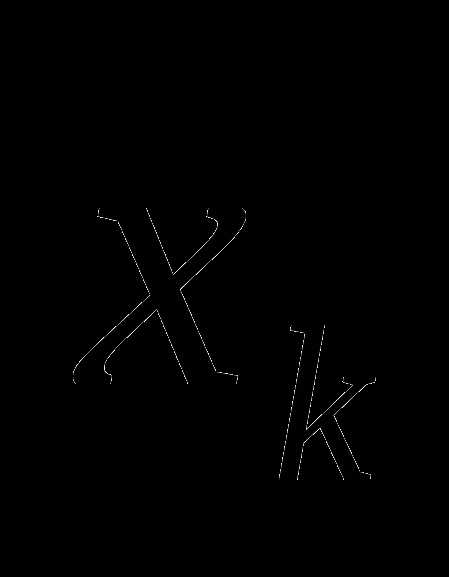 строятся по следующей рекуррентной формуле: (2) здесь
строятся по следующей рекуррентной формуле: (2) здесь 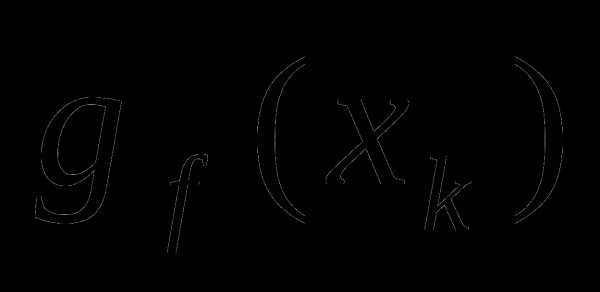 – произвольный субградиент функции
– произвольный субградиент функции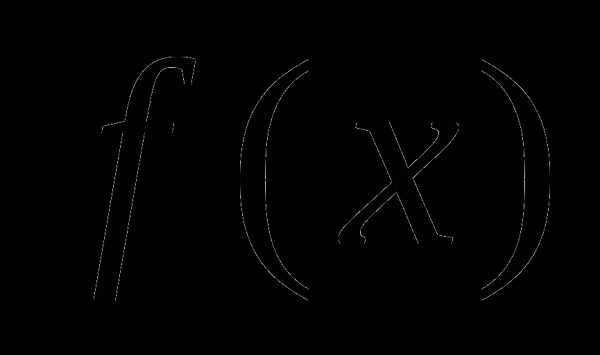 в точке
в точке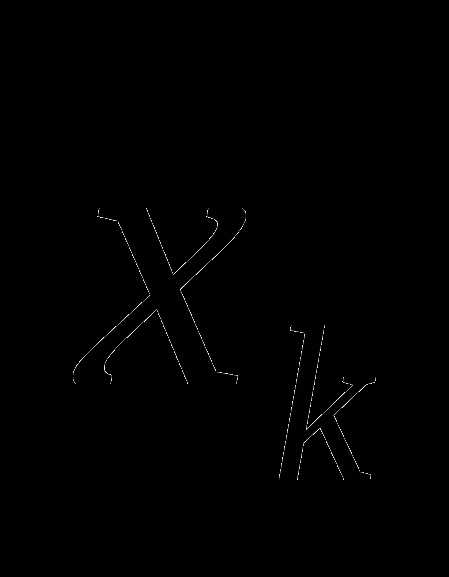 ,
, – шаговый множитель. Если
– шаговый множитель. Если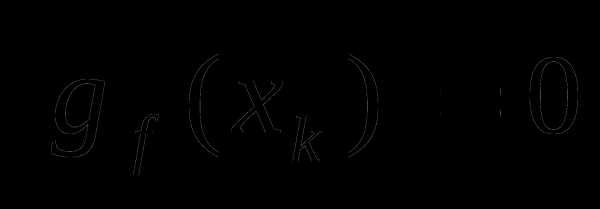 , то
, то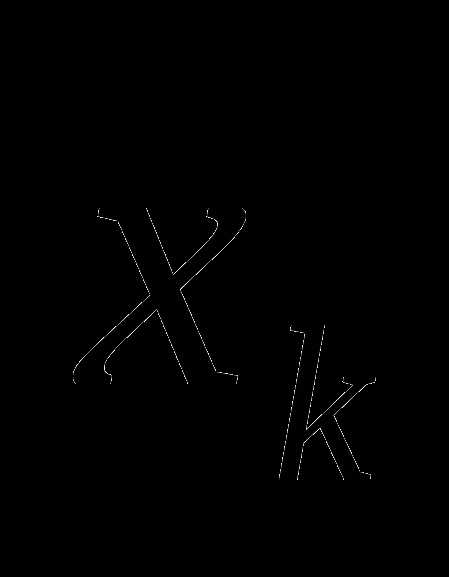 – есть точкой минимума функции
– есть точкой минимума функции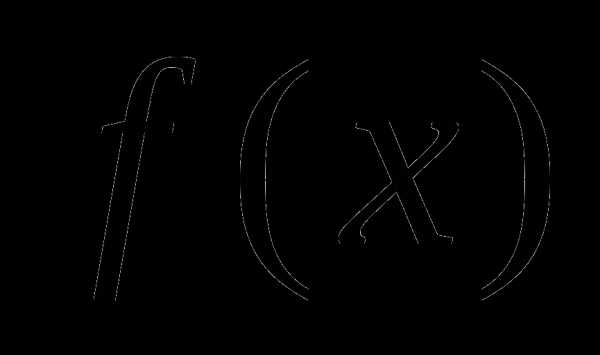 и процесс останавливается. В Институте кибернетики, начиная с 1962 года, были разработаны несколько вариантов ОГС, использующих соотношение (2). Эти результаты получены в период с 1962 по 1968 год и наиболее полно отражены в монографии [2], материал которой составила докторская диссертация Н.З.Шора 1970 года.
и процесс останавливается. В Институте кибернетики, начиная с 1962 года, были разработаны несколько вариантов ОГС, использующих соотношение (2). Эти результаты получены в период с 1962 по 1968 год и наиболее полно отражены в монографии [2], материал которой составила докторская диссертация Н.З.Шора 1970 года.
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме:, где—сжимающее отображение.
Для наилучшей сходимостиметода в точке очередного приближениядолжно выполняться условие. Решение данного уравнения ищут в виде, тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функциянепрерывна, окончательная формула длятакова:
С учётом этого функцияопределяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банахапоследовательность приближений стремится к корню уравнения.
Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.
Применительно к задачам о наименьших квадратах [править]
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .
Тогда очередное направление определяется из системы:
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезкеидифференцируемаяна нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где — угол наклона касательной в точке.
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к корню, тем лучше, но если предположения о его нахождении отсутствуют, методом проб и ошибок можно сузить область возможных значений, применивтеорему о промежуточных значениях).
Алгоритм
Задается начальное приближение .
Пока не выполнено условие остановки, в качестве которого можно взять или(то есть погрешность в нужных пределах), вычисляют новое приближение:.
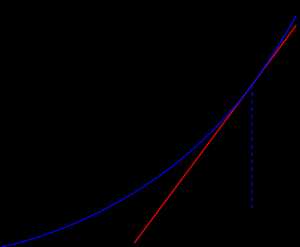
Метод наискорейшего спуска
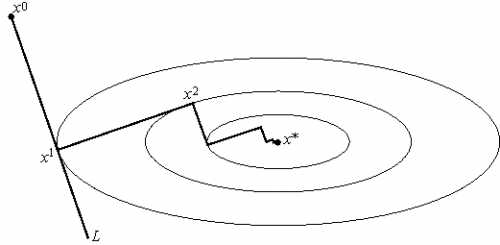
Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге выбирается так, чтобы следующая итерация была точкой минимума функциина луче L.
Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче:
.
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
значимыми. Это означает, что достигнута область оптимума.
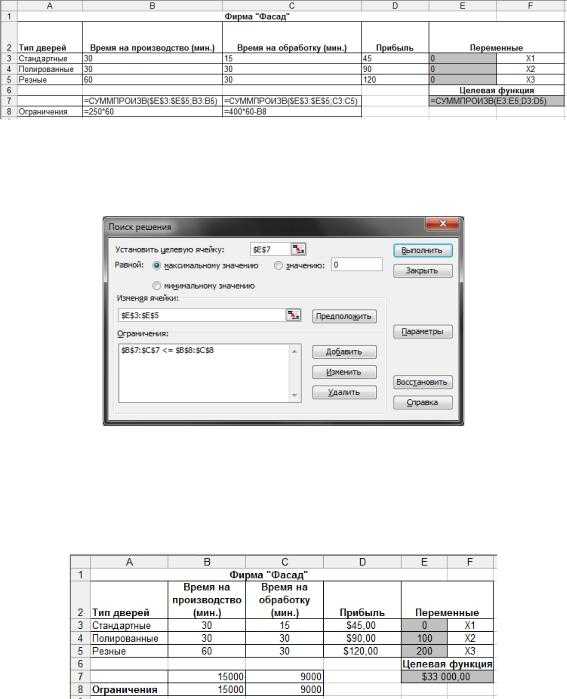
Пример:
Дана система лин. Уравнений
Зх1-5x2+x3+2x4 =1
2x1-2x2 +x4-x5=-4
X1-3x2-2x4-x5=-5
Ф=х1+2х2+х3+х4+х5
Требуется среди неотрицательных решений данной системы выбрать такое, которое минимизирует данную целевую функцию f.
Прежде всего замечаем, что переменная x3 входит только в первое уравнение системы и коэффициент при x3 имеет тот же знак, что и свободный член этого уравнения.
Поэтому разрешим это уравнение относительно x3
X3=1-(3x1-5x2+2x4)
Примем x3 одним из базисных неизвестных. Для остальных двух уравнений вводим искусственные переменные (неизвестные(у1 и у2). В результате:
x3=1-(3x1-5x2+2x4)
Y1=4-(-2x4+2x2-x4+x5)
Y2=5-(-x1+3x2-2x4+x5)
С помощью симплекс-метода минимизируем следующую функцию:
Ф=у1+у2=9-(-3х1+5х2+3х4+2х5)
Первая Симплекс-таблица имеет вид:
| ***** | |||||||||
| Базисные | Свободные | Х1 | Х2 | Х3 | Х4 | Х5 | У1 | У2 | |
| Х3 | 1 | 3 | -5 | 1 | 2 | 0 | 0 | 0 | |
| ***** | У1 | 4 | -2 | 2 | 0 | -1 | 1 | 1 | 0 |
| У2 | 5 | -1 | 3 | 0 | -2 | 1 | 0 | 1 | |
| Ф' | 9 | -3 | 5 | 0 | -3 | 2 | 0 | 0 | |
| Ф | 0 | -1 | -2 | 0 | 0 | 0 | 0 | 0 |
Последующие шаги имеет целью минимизацию Ф''. Целевая функция при этом преобразовании играет пассивную роль. Разрешающий элемент «1» выбираем в строке «у», и столбце «х5».
Таким образом, в результате первого шага неизвестное «у» выходит из базиса. Далее, поскольку столбцы «у1» и «у2» должны вычеркиваться на последнем шаге (после достижения минимума «Ф»), то столбец «у1» имеет смысл вычеркивать уже сейчас. Переходим к таблице 2.
| ***** | ***** | |||||||
| Базисные | Свободные | Х1 | Х2 | Х3 | Х4 | Х5 | У2 | |
| ***** | Х3 | 1 | 3 | -5 | 1 | 2 | 0 | 0 |
| Х5 | 4 | -2 | 2 | 0 | -1 | 1 | 0 | |
| ***** | У2 | 1 | 1 | 1 | 0 | -1 | 0 | 1 |
| Ф' | 1 | 1 | 1 | 0 | -1 | 0 | 0 | |
| Ф | 0 | 1 | -2 | 0 | 0 | 0 | 0 |
Таким образом, после второго шага оба искуственных неизвестных выходят из системы и становятся небазисными.
Этот факт уже свидетельствует о достижении минимума
minФ’=0
Так как в последнем базисном решении F=y1+y2
Отбрасываем столбец «у2» и строку «Ф» и переходим к следующей таблице 3.
| ***** | ||||||
| Базисные | Свободные | Х1 | Х2 | Х3 | Х4 | Х5 |
| Х1 | 6/8 | 1 | 0 | 1/8 | -3/8 | 0 |
| Х5 | 5 | 0 | 0 | ½ | -1/2 | 1 |
| Х2 | 2/8 | 0 | 1 | -1/8 | -5/8 | 0 |
| Ф | 10/8 | 0 | 0 | -1/8 | -13/8 | 0 |
Как видно, целевая функция Ф достигла минимума равного 10/8.
Оптимальное решение есть:
Х1=6/8; х5=5; х2=2/8; х3=х4=0.
studfiles.net
3.2. Градиентные методы
Другая группа методов, разработанная для решения задач безусловной оптимизации, состоит из градиентных методов. Их еще называют методами первого порядка, или методами спуска. Эти методы используют как значения функции, так и значения частных производных первого порядка, поэтому могут быть применены для минимизации только дифференцируемых функций. Методы первого порядка сходятся быстрее методов прямого поиска, так как в них учитываются производные, характеризующие направление наиболее быстрого убывания функции. Рассмотрим некоторые из них.
3.2.1. Метод наискорейшего спуска
Такой метод является одной из наиболее фундаментальных процедур минимизации дифференцируемых функций нескольких переменных.
В методе наискорейшего спуска в качестве направления поиска выбирается вектор, направление которого противоположно направлению вектора градиента функции 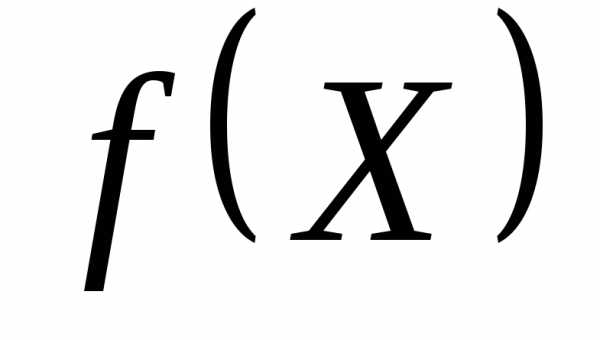 . Из математического анализа известно, что вектор
. Из математического анализа известно, что вектор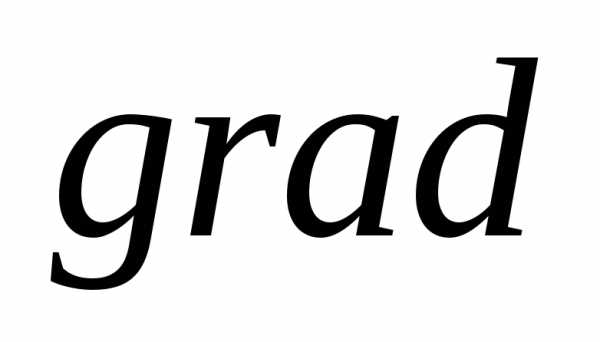 характеризует направление наиболее быстрого возрастания функции. Поэтому вектор
характеризует направление наиболее быстрого возрастания функции. Поэтому вектор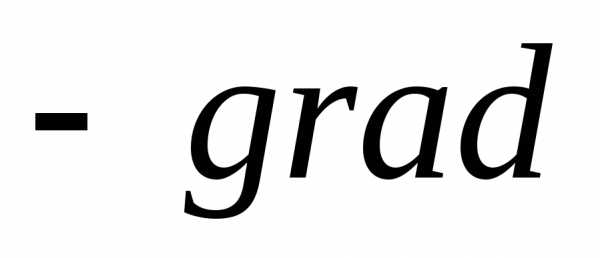 называется антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид
называется антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид
,
где  - величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шага
- величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шага фиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, если
фиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, если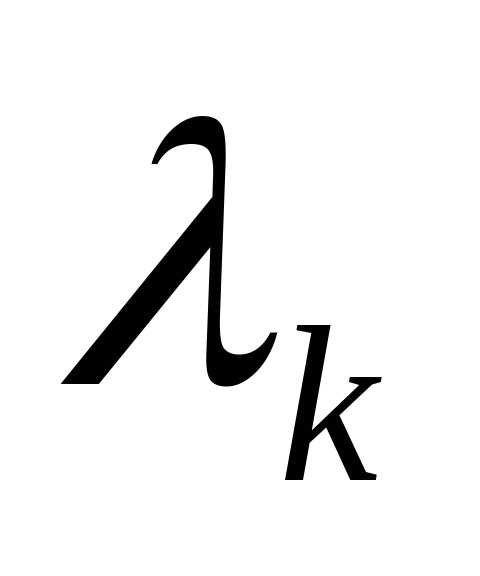 выбирать из условия
выбирать из условия
.
Для определения 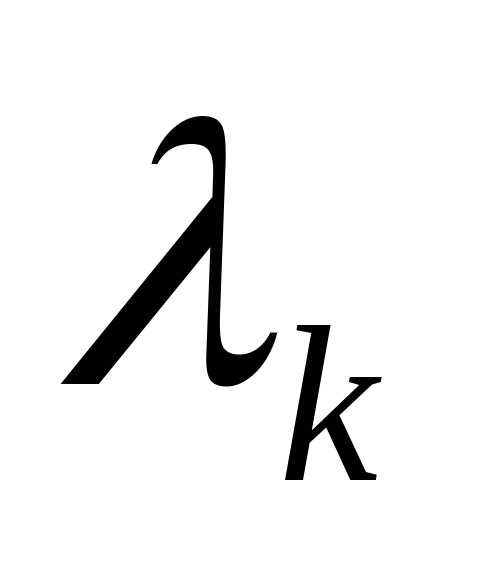 используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.
используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.
Рис. 14
Если пространство очень вытянуто по некоторым переменным, то образуется “овраг”. Поиск может замедлиться и идти зигзагами поперек дна “оврага” (рис. 14). Иногда решение невозможно получить за приемлемое время. Еще одним недостатком метода может быть критерий остановки , так как этому условию удовлетворяет и седловая точка, а не только оптимум.
Для ускорения сходимости градиентного метода в настоящее время разработано много различных приемов. Метод сопряженных градиентов один из них.
П ример.Щелкнув по значку, откроется Mathcad документ метода наискорейшего спуска, в котором можно выполнить вычисления.
ример.Щелкнув по значку, откроется Mathcad документ метода наискорейшего спуска, в котором можно выполнить вычисления.
Минимизация функции
методом наискорейшего спуска
Метод сопряженных градиентов Флетчера и Ривса
В этом методе направление спуска отклоняется от направления антиградиента за счет добавления к нему вектора направления, используемого на предыдущем шаге, умноженного на некоторое положительное число.
Направления поиска на каждой итерации определяются с помощью формулы.
,
где являются предыдущими направлениями поиска;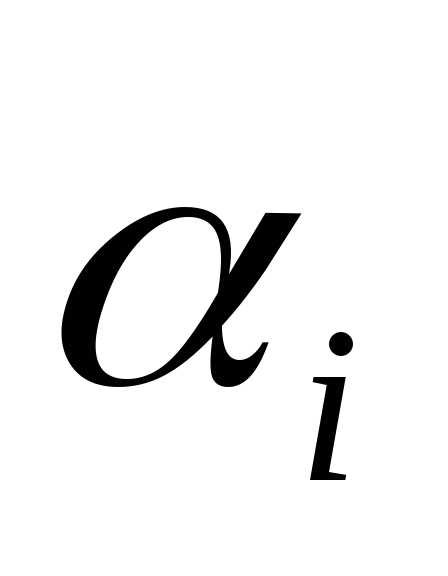 - параметрами. Значения параметров выбираются таким образом, чтобы направление
- параметрами. Значения параметров выбираются таким образом, чтобы направление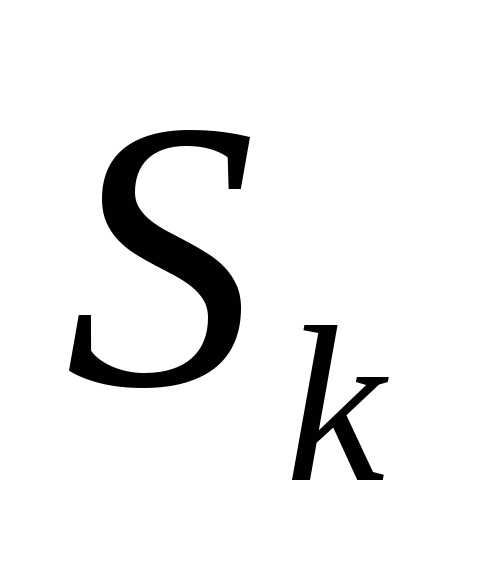 было
было -сопряженным со всеми построенными ранее направлениями поиска. Доказано, что это условие будет выполняться при
-сопряженным со всеми построенными ранее направлениями поиска. Доказано, что это условие будет выполняться при
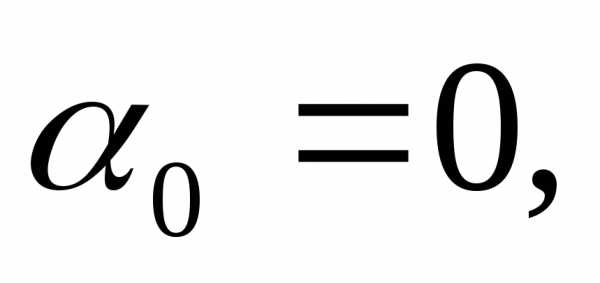

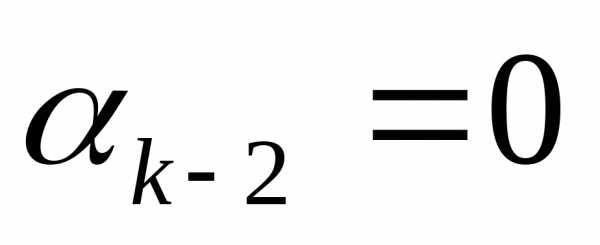 ,
,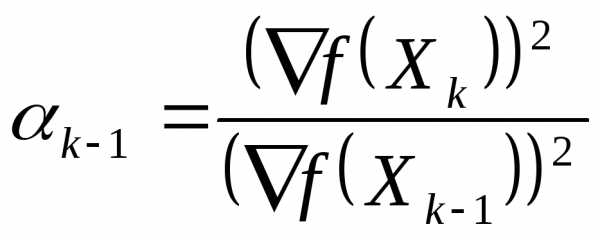 .
.
Если минимизируемая функция квадратичная и выпуклая, то алгоритм сопряженных градиентов приводит к оптимальному решению не более чем за n выполненных линейных поисков. Практические исследования показали, что этот метод сходится быстрее метода наискорейшего спуска, причем его эффективность возрастает на завершающих этапах поиска минимума функции. Кроме этого, следует отметить, что данный метод может быть использован при минимизации функций с разрывными производными. Поиск “не зависает на изломе”, а идет вдоль линии, соединяющей точки изломов линий уровня, которая, как правило, проходит через точку минимума.
Алгоритм.
Начальный этап. Выбрать число > 0 для остановки алгоритма и начальную точку 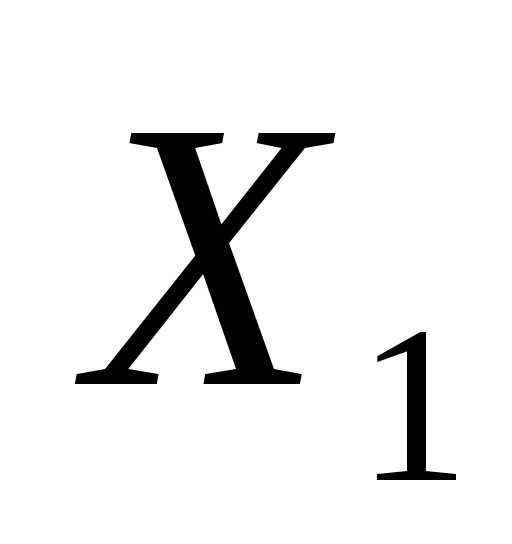 . Положить
. Положить  =
= 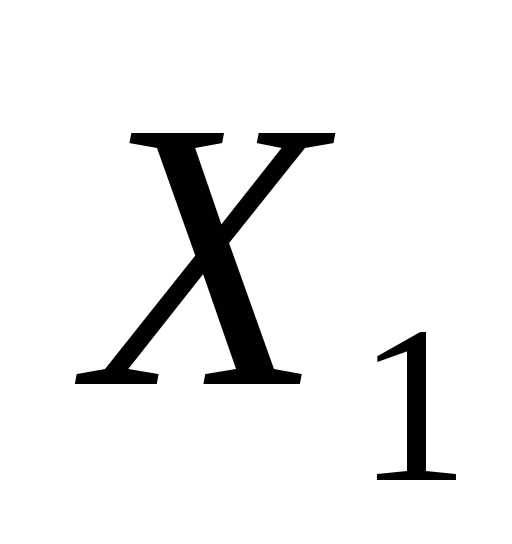 ,
, 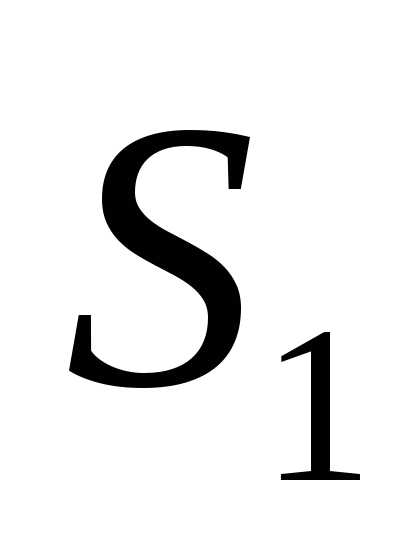 = -f(
= -f(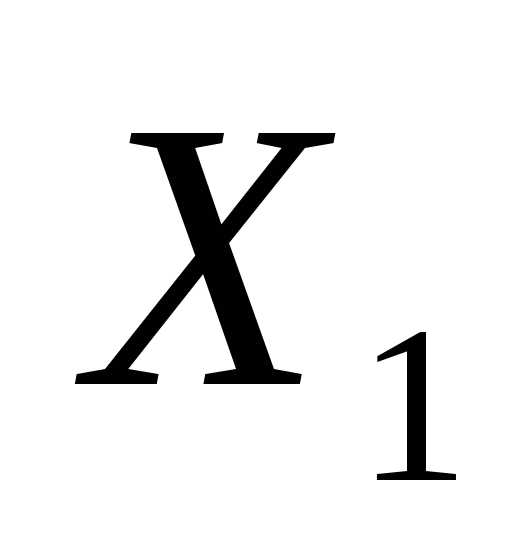 ), k = j = 1 и перейти к основному этапу.
), k = j = 1 и перейти к основному этапу.
Основной этап:
Шаг 1. Если ||f( )|| < , то минимум найден. В противном случае взять в качестве j оптимальное решение задачи минимизации функции f(
)|| < , то минимум найден. В противном случае взять в качестве j оптимальное решение задачи минимизации функции f(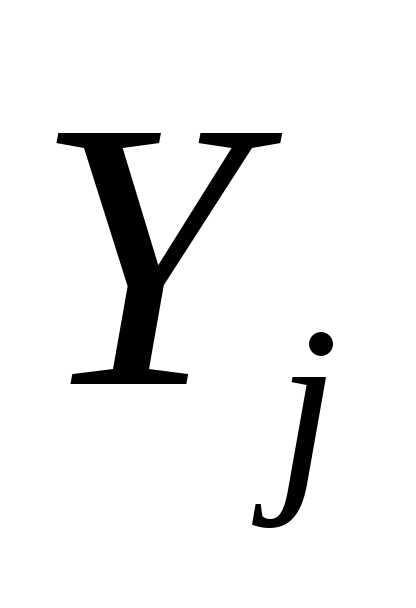 +
+ 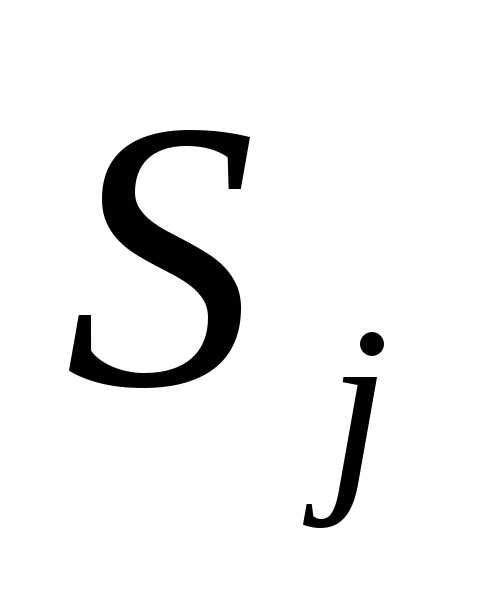 ) при 0 и положить
) при 0 и положить 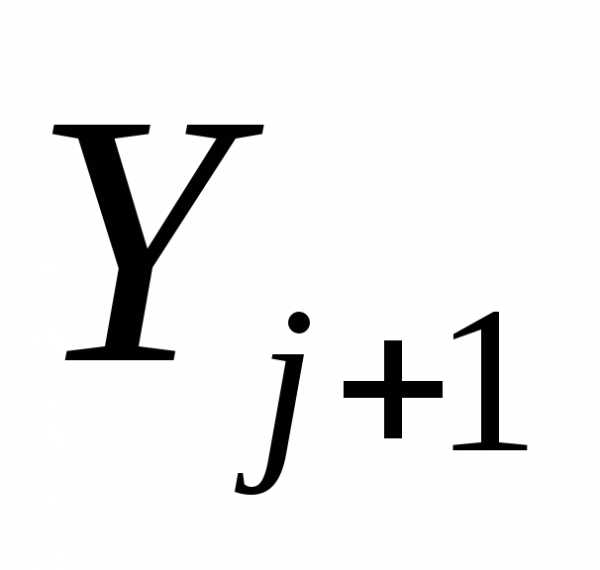 =
=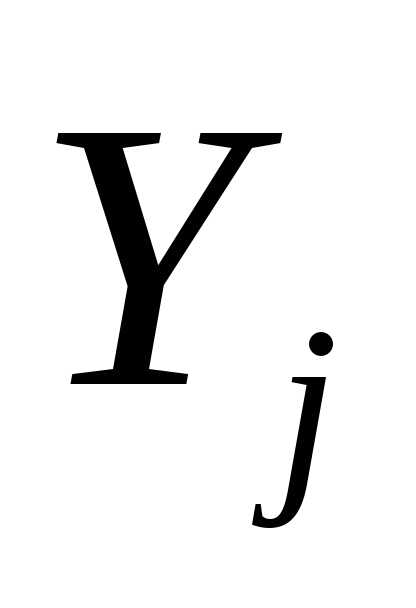 +j
+j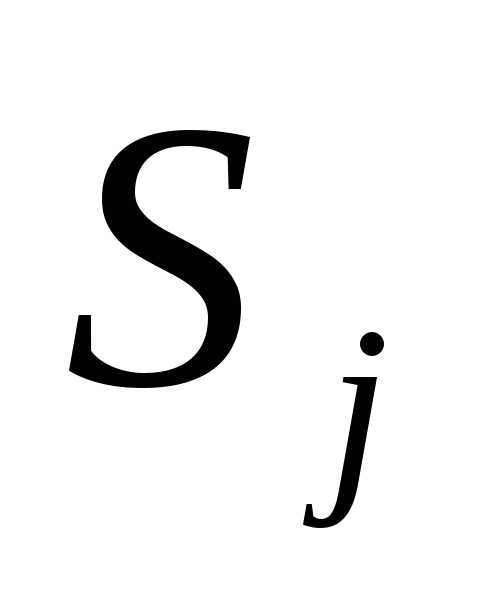 . Если
. Если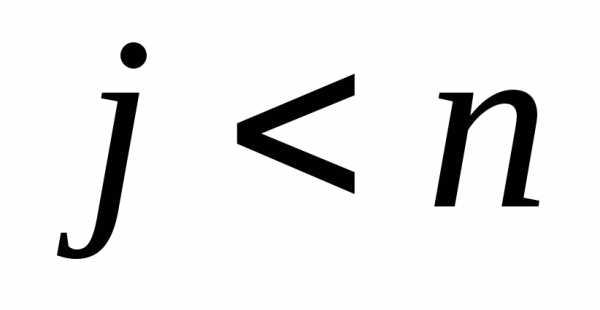 , то перейти к шагу 2; в противном случае перейти
, то перейти к шагу 2; в противном случае перейти
к шагу 3.
Шаг 2. Положить 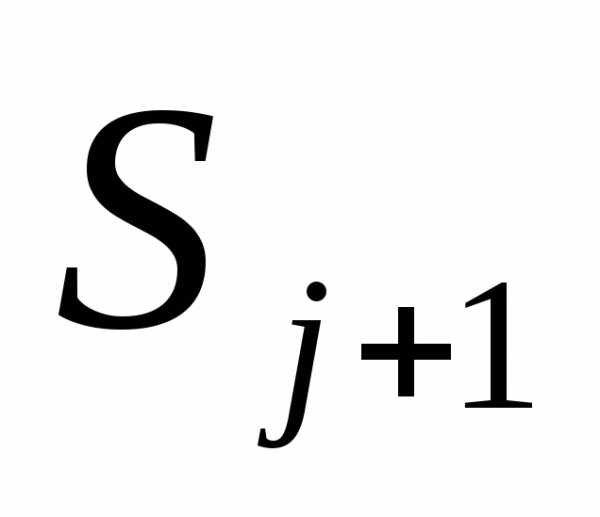 =-f(
=-f(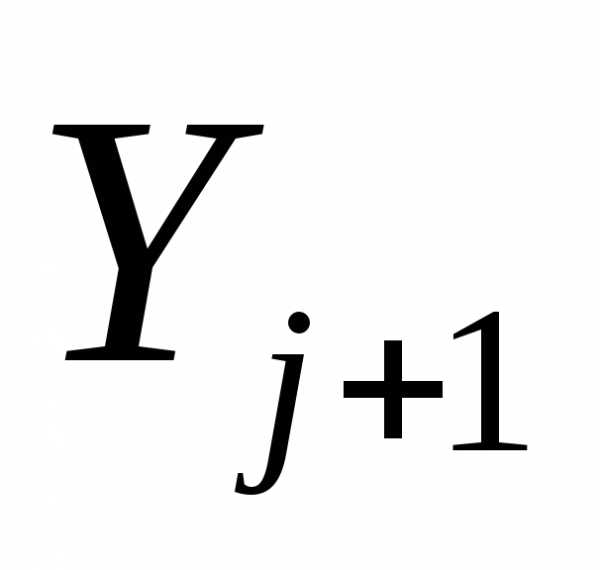 )+j
)+j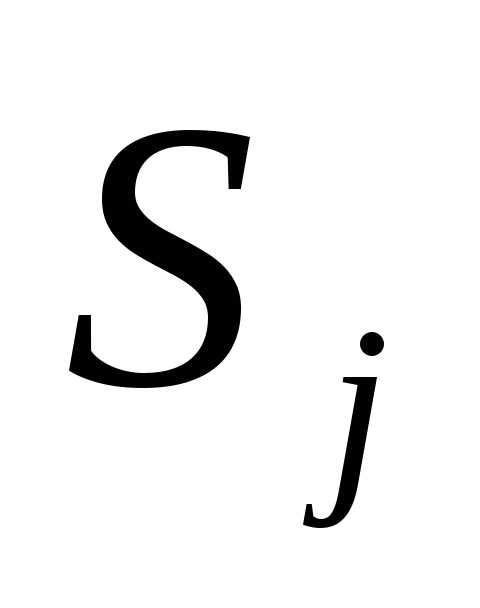 , где j=||f(
, где j=||f(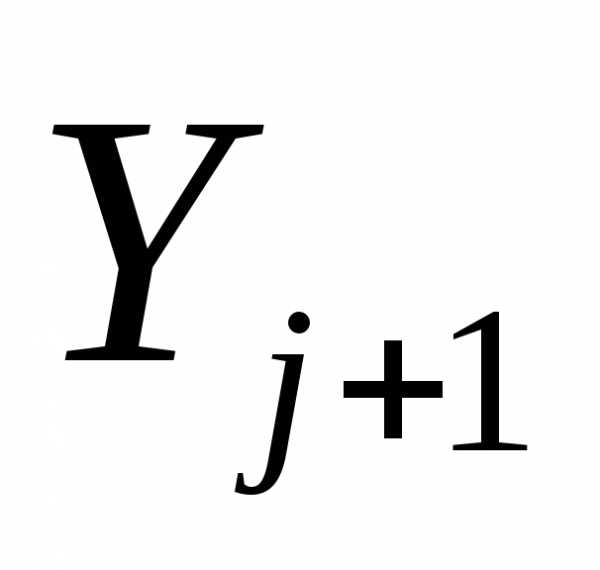 )||2/||f(
)||2/||f(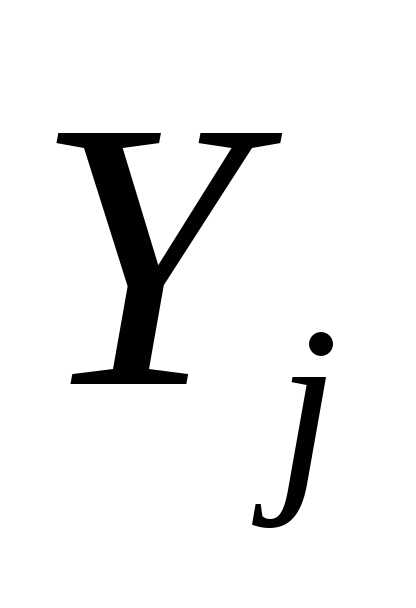 )||2. Заменить j на j + 1 и перейти к шагу 1.
)||2. Заменить j на j + 1 и перейти к шагу 1.
Шаг 3. Положить  =
= 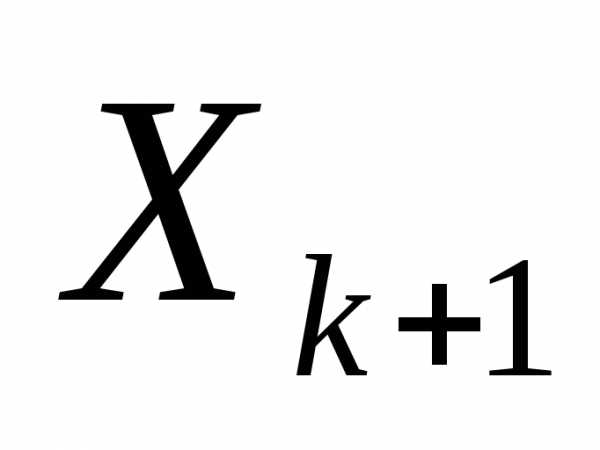 =
= 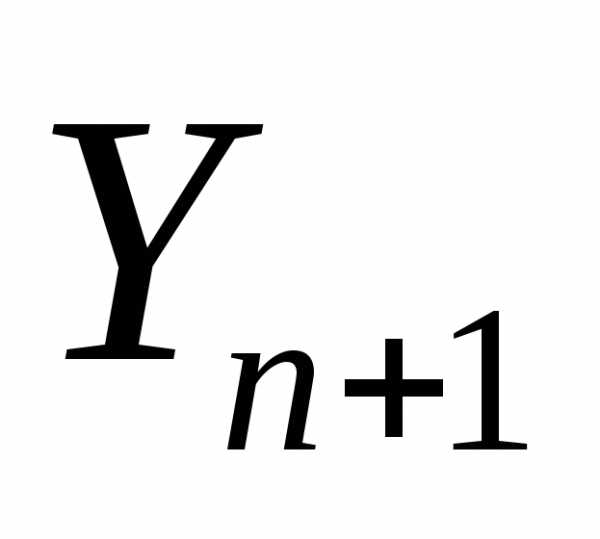 ,
, 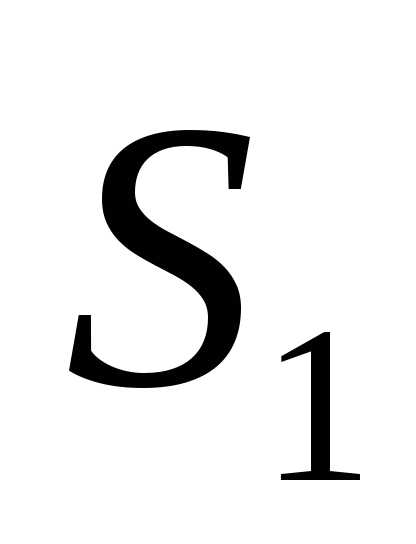 = - f(
= - f( ), j=1, к = к+1 и перейти к шагу 1.
), j=1, к = к+1 и перейти к шагу 1.
Пример. Щелкнув по значку, откроется Mathcad документ метода Флетчера-Ривса, в котором можно выполнить вычисления.
Минимизация функции
методом Флетчера – Ривса
studfiles.net
Градиентные методы минимизации функций многих переменных.
Лабораторная работа 3.
Постановка задачи: Требуется найти | безусловный минимум | функции n | ||||
переменных f (x) = f (x , x ,..., x ) , т.е. такую точкуx E | n | , что | f (x )= minf (x). | |||
1 2 | n |
|
| x En | ||
Предполагается, что целевая функция f (x) |
|
|
| |||
− дифференцируема в En | и возможно | |||||
вычисление ее производных в произвольной точке En .
В данной работе рассматриваются итерационные процедуры минимизации вида
xk+1 | = xk +αk pk ,k = 0,1,... | (1) |
где направление убывания | pk определяется тем или иным способом с учетом | |
информации о частных производных функции f (x) , а величина шагаαk > 0 такова, что
|
| f (xk +1 ) < f(xk ), | k =1,2,... | (2) |
|
| Метод градиентного спуска. | ||
Стратегия поиска: Положим в (1) на каждом шаге | pk = − f (xk ) . Еслиf (xk ) ≠ 0 , | |||
то условие | ( f (xk ), pk ) < 0 , очевидно, | выполнено. | Следовательно, направление | |
вектора pk | является | направлением убывания функции f (x) , причем в малой | ||
окрестности точки xk | направление pk | обеспечивает наискорейшее убывание этой | ||
функции. Поэтому найдется такое αk > 0 , что будет выполняться условие (2).
Для сильно выпуклых функций метод градиентного спуска гарантирует сходимость последовательности {xk }к точке минимумаx функцииf (x) . Скорость
сходимости метода − линейная. |
|
|
|
|
|
| |
Алгоритм: |
|
|
|
|
|
| |
1. | Задать параметр точности ε > 0 , начальный шагα >0 , выбратьx En . Вычислить | ||||||
f (x) . |
|
|
|
|
|
| |
2. | Вычислить f (x) и проверить условие достижения точности: |
| f (x) |
|
|
| <ε . Если оно |
|
|
| |||||
выполнено, вычисления завершить, положив x = x , f = f (x) . | Иначе – перейти к | ||||||
шагу 3. |
|
|
|
|
|
| |
3. | Найти y = x −α f (x) иf (y) . Еслиf (y) < f (x) , то положитьx = y , |
| f (x) = f(y) и | ||||
перейти к шагу 2, иначе − к шагу 4. |
|
|
|
|
|
| |
4. | Положить α =α / 2 и перейти к шагу 3. |
|
|
|
|
|
|
Замечание. Вблизи стационарной точки функцииf (x) величина f (x)становится малой. Это часто приводит к замедлению сходимости последовательности{xk }. Поэтому в основной формуле (1) иногда полагаютpk = −f (xk ) / f (xk ), используя вместо антиградиента вектор единичной длины в этом же направлении.
1
Метод наискорейшего спуска.
Стратегия поиска: Метод является модификацией метода градиентного спуска. Здесь также полагаютpk = − f (xk ) , но величина шагаαk из (1) находится в результате решения задачи одномерной оптимизации
Φ | k | α | → | min , | Φ | α | = | f (x | k −α | f (x | k | )), | α > | 0 | , | (3) |
| ( ) |
|
| k ( ) |
|
|
|
|
| |||||||
т.е. на каждой | итерации | в | направлении антиградиента |
| − f (xk ) совершается | |||||||||||
исчерпывающий спуск.
Для сильно выпуклых функций метод наискорейшего спуска гарантирует сходимость последовательности {xk }к точке минимумаx функцииf (x) . Скорость сходимости метода − линейная.
Алгоритм:
1. Задать параметр точности ε >0 , выбратьx En . Вычислитьf (x) .
2. Вычислить f (x) и проверить условие достижения точности: f (x) <ε . Если оно
выполнено, вычисления завершить, полагая x = x , f = f (x) . Иначе – перейти к шагу 3.
3. Решить задачу одномерной оптимизации (3) для xk = x , т.е. найтиα . Положитьx = x −α f (x) и перейти к шагу 2.
Замечание. Решение задачи (3) можно получить одним из рассмотренных для одномерной минимизации способов. Проверять выполнение условия (2) в этом
методе необязательно. Если функция f (x) квадратична, т.е.f (x) = 12 (Ax, x) + (b,x) + c , то для величины шага исчерпывающего спуска можно получить точную формулу
αk = − | ( f (xk ),pk ) | = − | (Axk + b,pk ) | , положив | pk = − f(xk ) . |
(Apk ,pk ) |
| ||||
|
| (Apk ,pk ) |
| ||
На практике, значения многих исследуемых функций вдоль некоторых направлений изменяются гораздо быстрее (иногда на несколько порядков), чем в других направлениях. Их поверхности уровня сильно вытягиваются, а в более сложных случаях изгибаются и представляют собой овраги. Направление антиградиента у овражных функций существенно отклоняется от направления в точку минимума, что приводит к замедлению скорости сходимости.
Скорость сходимости градиентных методов существенно зависит также от точности вычислений градиента. Потеря точности, а это обычно происходит в окрестности точек минимума или в овражной ситуации, может вообще нарушить сходимость процесса градиентного спуска.
Вследствие перечисленных причин градиентные методы зачастую используются в комбинации с другими, более эффективными методами на начальной стадии решения задачи. В этом случае точка x0 находится далеко от точки минимума, и шаги в направлении антиградиента позволяют достичь существенного убывания функции.
2
Метод сопряженных градиентов.
Стратегия поиска: В методах градиентного спуска в итерационной процедуре (1) в качестве направления убывания функцииf (x) использовалось направление
антиградиента: pk = − f (xk ) . Однако такой выбор направления убывания не всегда бывает удачным. В частности, для плохо обусловленных задач минимизации направление антиградиента в точкеxk может значительно отличаться от
направления к точке минимума x . В результате, траектория приближения к точке минимума имеет зигзагообразный характер. В методе сопряженных градиентов применяется другой подход. Используется итерационный процесс
xk+1 = xk+αk pk | , |
|
| k = 0,1,...; | x0 En , | p0 = − f(x0 ) , |
|
| ||||||||||||||
в котором величина шага | αk находится из условия исчерпывающего спуска по | |||||||||||||||||||||
направлению pk : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk | +αk pk )= minf (xk | +αpk ), | k = 0,1,.... |
|
| |||||||||||||||||
|
|
|
|
|
| α>0 |
|
|
|
|
|
|
|
|
| |||||||
Далее, после вычисления очередной точки | xk+1 , | k = 0,1,..., новое направление | ||||||||||||||||||||
поиска pk+1 находится по формуле, отличной от антиградиента: |
|
| ||||||||||||||||||||
pk+1 | = − f (xk +1 ) +βk | pk | , | k = 0,1,..., |
|
|
| |||||||||||||||
где коэффициенты | βk | выбираются так, | чтобы при минимизации квадратичной | |||||||||||||||||||
функции f (x) с | положительно |
| определенной | матрицей | A | получалась | ||||||||||||||||
последовательность A - ортогональных векторовp0 , p1 ,... . |
|
| ||||||||||||||||||||
Одна из возможных формул для коэффициента βk | имеет вид |
|
| |||||||||||||||||||
|
| βk | = |
| f (xk +1 ) |
|
|
| 2 | , | k =1,2,... |
|
|
| ||||||||
|
|
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
| f (xk ) |
|
|
| 2 |
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
| ||||||||||||||
Выражение для | коэффициента | βkне | содержит | в явном | виде | матрицу A | ||||||||||||||||
квадратичной формы. Поэтому метод сопряженных градиентов применяют для минимизации любых, а не только квадратичных функций.
Если функция f (x) квадратична, т.е.f (x) = 12 (Ax, x) + (b,x) + c , то для величины шага исчерпывающего спуска можно получить точную формулу
αk = − (f (xkk ),pk k ).
(Ap, p)
При реализации метода сопряженных градиентов применяется практический прием – через каждыеN шагов производят обновление метода, полагаяβm N =0, m =1,2,.... Номераm N называют моментамирестарта. Часто полагают
N = n - размерности пространстваEn . ЕслиN =1, то получаетсячастный случай метода сопряженных градиентов – метод наискорейшего спуска.
Алгоритм:
1.Задать точность вычислений ε , выбрать начальное приближениеx0 и частоту обновленияN .
2.Положить k = 0 (k - номер итерации). Вычислить значениеp0 = − f (x0 ) .
3

3.Вычислить значение αk из решения задачи одномерного исчерпывающего спуска
f (xk +αk | pk )= min | f (xk | +α pk ) , либо другим методом |
| α>0 |
|
|
4.Вычислить точку xk +1 | = xk +αk pk и градиентf (xk +1 ) . | ||
5.Проверить критерий окончания поиска f (xk +1 ) < ε . Если критерий выполнен,
перейти к шагу 8.
6.Если k +1 = N , то положитьx0 = xk +1 , и перейти к шагу 2 (рестарт).
7.Вычислить коэффициент βk по выбранной формуле и найти новое направление
поиска pk +1 | = − f (xk +1 ) + βk pk . Положитьk = k +1 и перейти к шагу 3. |
|
|
|
| ||||||||
8.Выбрать приближенно x | = xk +1 , f (x ) = f (xk +1 ) . Поиск завершен. |
|
|
|
| ||||||||
Дополнительные сведения о методе сопряженных градиентов |
| ||||||||||||
1.Минимизация квадратичных функций |
|
| f (x) = cT x+ 1 |
|
|
| |||||||
Рассмотрим задачу поиска минимума квадратичной функции: | 2 | xT Ax , где | |||||||||||
A – симметричная положительно определенная матрица. |
|
|
|
|
| ||||||||
|
|
|
|
|
| ||||||||
Обозначим для краткости g i | = f (xi ) - вектор градиента, | yi = g i+1 − g i ,pi - направление | |||||||||||
спуска в формуле xi+1 = xi +αi pi . |
|
|
|
|
|
|
|
|
| ||||
Рассмотрим набор | A – сопряженных ненулевых векторов, | то есть: ( pi )T Ap j = 0 | для всех | ||||||||||
i ≠ j . Так как эти вектора | A – сопряжены, то они являются линейно независимыми. | ||||||||||||
Действительно, если представить один из этих векторов | pk как линейную комбинацию | ||||||||||||
остальных: | pk | = a0 p0 +... +ak −1 pk −1 , | то | при | умножении | этого равенства на | ( pi )T A , | ||||||
получим, что ( pi )T Apk = a0 (pi )T Ap0 | +...+ ak −1 (pi )T Apk −1 | = 0 , | что невозможно, | так как | |||||||||
pk ≠ 0 иA – положительно определенная матрица. |
|
|
|
|
|
| |||||||
Для рассмотренного набора | A – сопряженных направлений | соответствующий метод | |||||||||||
сопряженных | направлений | выглядит | так: | xk+1 = xk+αk pk. | (Можно доказать, что | ||||||||
последовательный исчерпывающий спуск по A – ортогональным направлениям приводит | |||||||||||||
к точке минимума квадратичной формы не более чем за n шагов) |
|
|
|
| |||||||||
По свойствам | квадратичной | функции f (x) | для любых точек xi+1 и | xi, |
| связанных | |||||||
равенством xi+1 | = xi +αi pi , имеем:yi | = f (xi+1 ) −f (xi ) =A(xi+1 −xi ) =αi | Api . |
|
| ||||||||
Получаем, | что | условие | сопряженности | ( pi)TAp j | = 0 | эквивалентно |
| условию | |||||
ортогональности: (yi )T p j = 0 . |
|
|
|
|
|
|
|
|
| ||||
Докажем теперь, | что направление pk | для очередной итерации можно вычислять как | |||||||||||
линейную комбинацию градиента в текущей точке xk и предыдущего направленияpk −1 . Доказываем методом математической индукции.
Пусть | p0 | совпадает в начальной точке с антиградиентом − g 0 в начальной точке | x0. | ||||
Пусть | k | шагов метода спуска по взаимно сопряженным направлениям p0 ,...,pk −1 | уже | ||||
выполнены, причем каждый из векторов | pi был суммой антиградиента− g i и линейной | ||||||
комбинации | p0 ,...,pi−1 . Направление | pk | для очередного шага тоже будем искать в таком | ||||
|
|
| k−1 |
|
|
|
|
виде: | pk = −g k + ∑βki pi . Из этой формулы следует, что | g k - это линейная комбинация | |||||
|
|
| i=0 |
|
|
|
|
направлений | p0 ,...,pk . Учитывая | (g i )T pi = 0 , можно | утверждать (g k )T g i = 0,i < k . | ||||
|
|
|
|
|
|
| 4 |
studfiles.net
Градиентные методы безусловной оптимизации используют только первые производные целевой функции и являются методами линейной аппроксимации на каждом шаге, т е
Градиентные методыГрадиентные методы безусловной оптимизации используют только первые производные целевой функции и являются методами линейной аппроксимации на каждом шаге, т.е. целевая функция на каждом шаге заменяется касательной гиперплоскостью к ее графику в текущей точке.На k-м этапе градиентных методов переход из точки Xk в точку Xk+1 описывается соотношением:
Xk+1= Xk+ kSk, (1.2)
где k- величина шага, k- вектор в направлении Xk+1-Xk.Методы наискорейшего спуска
Впервые такой метод рассмотрел и применил еще О. Коши в XVIII в. Идея его проста: градиент целевой функции f(X) в любой точке есть вектор в направлении наибольшего возрастания значения функции. Следовательно, антиградиент будет направлен в сторону наибольшего убывания функции и является направлением наискорейшего спуска. Антиградиент (и градиент) ортогонален поверхности уровня f(X) в точке X. Если в (1.2) ввести направление
,
то это будет направление наискорейшего спуска в точке Xk.
Получаем формулу перехода из Xk в Xk+1:
.
Антиградиент дает только направление спуска, но не величину шага. В общем случае один шаг не дает точку минимума, поэтому процедура спуска должна применяться несколько раз. В точке минимума все компоненты градиента равны нулю.
Все градиентные методы используют изложенную идею и отличаются друг от друга техническими деталями: вычисление производных по аналитической формуле или конечно-разностной аппроксимации; величина шага может быть постоянной, меняться по каким-либо правилам или выбираться после применения методов одномерной оптимизации в направлении антиградиента и т.д. и т.п.
Останавливаться подробно мы не будем, т.к. метод наискорейшего спуска не рекомендуется обычно в качестве серьезной оптимизационной процедуры.
Одним из недостатков этого метода является то, что он сходится к любой стационарной точке, в том числе и седловой, которая не может быть решением.
Но самое главное - очень медленная сходимость наискорейшего спуска в общем случае. Дело в том, что спуск является "наискорейшим" в локальном смысле. Если гиперпространство поиска сильно вытянуто ("овраг"), то антиградиент направлен почти ортогонально дну "оврага", т.е. наилучшему направлению достижения минимума. В этом смысле прямой перевод английского термина "steepest descent", т.е. спуск по наиболее крутому склону более соответствует положению дел, чем термин "наискорейший", принятый в русскоязычной специальной литературе. Одним из выходов в этой ситуации является использование информации даваемой вторыми частными производными. Другой выход - изменение масштабов переменных.Метод сопряженного градиента Флетчера-Ривса
В методе сопряженного градиента строится последовательность направлений поиска , являющихся линейными комбинациями , текущего направления наискорейшего спуска, и , предыдущих направлений поиска, т.е.
,
причем коэффициенты выбираются так, чтобы сделать направления поиска сопряженными. Доказано, что
и это очень ценный результат, позволяющий строить быстрый и эффективный алгоритм оптимизации.
Алгоритм Флетчера-Ривса.
1. В X0 вычисляется .
2. На k-ом шаге с помощь одномерного поиска в направлении находится минимум f(X), который и определяет точку Xk+1.
3. Вычисляются f(Xk+1) и .
4. Направление определяется из соотношения:
5. После (n+1)-й итерации (т.е. при k=n) производится рестарт: полагается X0=Xn+1 и осуществляется переход к шагу 1.
6. Алгоритм останавливается, когда , где - произвольная константа.
Преимуществом алгоритма Флетчера-Ривса является то, что он не требует обращения матрицы и экономит память ЭВМ, так как ему не нужны матрицы, используемые в Ньютоновских методах, но в то же время почти столь же эффективен как квази-Ньютоновские алгоритмы. Т.к. направления поиска взаимно сопряжены, то квадратичная функция будет минимизирована не более, чем за n шагов. В общем случае используется рестарт, который позволяет получать результат.
Алгоритм Флетчера-Ривса чувствителен к точности одномерного поиска, поэтому при его использовании необходимо устранять любые ошибки округления, которые могут возникнуть. Кроме того, алгоритм может отказать в ситуациях, где Гессиан становится плохо обусловленным. Гарантии сходимости всегда и везде у алгоритма нет, хотя практика показывает, что почти всегда алгоритм дает результат.Ньютоновские методы
Направление поиска, соответствующее наискорейшему спуску, связано с линейной аппроксимацией целевой функции. Методы, использующие вторые производные, возникли из квадратичной аппроксимации целевой функции, т. е. при разложении функции в ряд Тейлора отбрасываются члены третьего и более высоких порядков.
,
где - матрица Гессе.
Минимум правой части (если он существует) достигается там же, где и минимум квадратичной формы. Запишем формулу для определения направления поиска :
.
Минимум достигается при .
Алгоритм оптимизации, в котором направление поиска определяется из этого соотношения, называется методом Ньютона, а направление - ньютоновским направлением.
В задачах поиска минимума произвольной квадратичной функции с положительной матрицей вторых производных метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки.
Классификация Ньютоновских методов
Собственно метод Ньютона состоит в однократном применении Ньютоновского направления для оптимизации квадратичной функции. Если же функция не является квадратичной, то верна следующая теорема.
Теорема 1.4. Если матрица Гессе нелинейной функции f общего вида в точке минимума X* положительно определена, начальная точка выбрана достаточно близко к X* и длины шагов подобраны верно, то метод Ньютона сходится к X* с квадратичной скоростью.
Метод Ньютона считается эталонным, с ним сравнивают все разрабатываемые оптимизационные процедуры. Однако метод Ньютона работоспособен только при положительно определенной и хорошо обусловленной матрицей Гессе (определитель ее должен быть существенно больше нуля, точнее отношение наибольшего и наименьшего собственных чисел должно быть близко к единице). Для устранения этого недостатка используют модифицированные методы Ньютона, использующие ньютоновские направления по мере возможности и уклоняющиеся от них только тогда, когда это необходимо.
Общий принцип модификаций метода Ньютона состоит в следующем: на каждой итерации сначала строится некоторая "связанная" с положительно определенная матрица , а затем вычисляется по формуле . Так как положительно определена, то - обязательно будет направлением спуска. Процедуру построения организуют так, чтобы она совпадала с матрицей Гессе, если она является положительно определенной. Эти процедуры строятся на основе некоторых матричных разложений.
Другая группа методов, практически не уступающих по быстродействию методу Ньютона, основана на аппроксимации матрицы Гессе с помощью конечных разностей, т.к. не обязательно для оптимизации использовать точные значения производных. Эти методы полезны, когда аналитическое вычисление производных затруднительно или просто невозможно. Такие методы называются дискретными методами Ньютона.
Залогом эффективности методов ньютоновского типа является учет информации о кривизне минимизируемой функции, содержащейся в матрице Гессе и позволяющей строить локально точные квадратичные модели целевой функции. Но ведь возможно информацию о кривизне функции собирать и накапливать на основе наблюдения за изменением градиента во время итераций спуска. Соответствующие методы, опирающиеся на возможность аппроксимации кривизны нелинейной функции без явного формирования ее матрицы Гессе, называют квази-Ньютоновскими методами.
Отметим, что при построении оптимизационной процедуры ньютоновского типа (в том числе и квази-Ньютоновской) необходимо учитывать возможность появления седловой точки. В этом случае вектор наилучшего направления поиска будет все время направлен к седловой точке, вместо того, чтобы уходить от нее в направлении "вниз". Метод Ньютона-Рафсона
Данный метод состоит в многократном использовании Ньютоновского направления при оптимизации функций, не являющихся квадратичными.
Основная итерационная формула многомерной оптимизации Xk+1= Xk+ k+1 используется в этом методе при выборе направления оптимизации из соотношения , k+1 = 1.
Реальная длина шага скрыта в ненормализованном Ньютоновском направлении . Так как этот метод не требует значения целевой функции в текущей точке, то его иногда называют непрямым или аналитическим методом оптимизации. Его способность определять минимум квадратичной функции за одно вычисление выглядит на первый взгляд исключительно привлекательно. Однако это "одно вычисление" требует значительных затрат. Прежде всего, необходимо вычислить n частных производных первого порядка и n(n+1)/2 - второго. Кроме того, матрица Гессе должна быть инвертирована. Это требует уже порядка n3 вычислительных операций. С теми же самыми затратами методы сопряженных направлений или методы сопряженного градиента могут сделать порядка n шагов, т.е. достичь практически того же результата. Таким образом, итерация метода Ньютона-Рафсона не дает преимуществ в случае квадратичной функции.
Если же функция не квадратична, то
- начальное направление уже, вообще говоря, не указывает действительную точку минимума, а значит, итерации должны повторяться неоднократно;
- шаг единичной длины может привести в точку с худшим значением целевой функции, а поиск может выдать неправильное направление, если, например, гессиан не является положительно определенным;
- гессиан может стать плохо обусловленным, что сделает невозможным его инвертирование, т.е. определение направления для следующей итерации.
Сама по себе стратегия не различает, к какой именно стационарной точке (минимума, максимума, седловой) приближается поиск, а вычисления значений целевой функции, по которым можно было бы отследить, не возрастает ли функция, не делаются. Значит, все зависит от того, в зоне притяжения какой стационарной точки оказывается стартовая точка поиска. Стратегия Ньютона-Рафсона редко используется сама по себе без модификации того или иного рода. Методы Пирсона
Пирсон предложил несколько методов с аппроксимацией обратного гессиана без явного вычисления вторых производных, т.е. путем наблюдений за изменениями направления антиградиента. При этом получаются сопряженные направления. Эти алгоритмы отличаются только деталями. Приведем те из них, которые получили наиболее широкое распространение в прикладных областях.
Алгоритм Пирсона № 2.
В этом алгоритме обратный гессиан аппроксимируется матрицей Hk, вычисляемой на каждом шаге по формуле
Hk+1 = Hk + .
В качестве начальной матрицы H0 выбирается произвольная положительно определенная симметрическая матрица.
Данный алгоритм Пирсона часто приводит к ситуациям, когда матрица Hk становится плохо обусловленной, а именно - она начинает осцилировать, колеблясь между положительно определенной и не положительно определенной, при этом определитель матрицы близок к нулю. Для избежания этой ситуации необходимо через каждые n шагов перезадавать матрицу, приравнивая ее к H0.
Алгоритм Пирсона № 3.
В этом алгоритме матрица Hk+1 определяется из формулы
Hk+1 = Hk + [Xk+1-Xk-Hk (f(Xk+1)- f(Xk))]
Траектория спуска, порождаемая алгоритмом, аналогична поведению алгоритма Дэвидона-Флетчера-Пауэлла, но шаги немного короче. Пирсон также предложил разновидность этого алгоритма с циклическим перезаданием матрицы.
Проективный алгоритм Ньютона-Рафсона
Пирсон предложил идею алгоритма, в котором матрица рассчитывается из соотношения
Hk+1 = Hk + ,
H0=R0, где матрица R0 такая же как и начальные матрицы в предыдущих алгоритмах.
Когда k кратно числу независимых переменных n, матрица Hk заменяется на матрицу Rk+1, вычисляемую как сумма
Rk +.
Величина Hk(f(Xk+1) - f(Xk)) является проекцией вектора приращения градиента (f(Xk+1)-f(Xk)), ортогональной ко всем векторам приращения градиента на предыдущих шагах. После каждых n шагов Rk является аппроксимацией обратного гессиана H-1(Xk), так что в сущности осуществляется (приближенно) поиск Ньютона. Метод Дэвидона-Флетчера-Пауэла
Этот метод имеет и другие названия - метод переменной метрики, квазиньютоновский метод, т.к. он использует оба эти подхода.
Метод Дэвидона-Флетчера-Пауэла (ДФП) основан на использовании ньютоновских направлений, но не требует вычисления обратного гессиана на каждом шаге. Направление поиска на шаге k является направлением , где Hi- положительно определенная симметричная матрица, которая обновляется на каждом шаге и в пределе становится равной обратному гессиану. В качестве начальной матрицы H обычно выбирают единичную. Итерационная процедура ДФП может быть представлена следующим образом:
1. На шаге k имеются точка Xk и положительно определенная матрица Hk.
2. В качестве нового направления поиска выбирается
3. Одномерным поиском (обычно кубической интерполяцией) вдоль направления определяется k, минимизирующее функцию .
4. Полагается .
5. Полагается .
6. Определяется и . Если Vk или достаточно малы, процедура завершается.
7. Полагается Uk= f(Xk+1) - f(Xk).
8. Матрица Hk обновляется по формуле
9. Увеличить k на единицу и вернуться на шаг 2.
Метод эффективен на практике, если ошибка вычислений градиента невелика и матрица Hk не становится плохо обусловленной.
Матрица Ak обеспечивает сходимость Hk к G-1, матрица Bk обеспечивает положительную определенность Hk+1 на всех этапах и в пределе исключает H0.
В случае квадратичной функции , т.е. алгоритм ДФП использует сопряженные направления.
Таким образом, метод ДФП использует как идеи ньютоновского подхода, так и свойства сопряженных направлений, и при минимизации квадратичной функции сходится не более чем за n итераций. Если оптимизируемая функция имеет вид, близкий к квадратичной функции, то метод ДФП эффективен за счет хорошей аппроксимации G-1(метод Ньютона). Если же целевая функция имеет общий вид, то метод ДФП эффективен за счет использования сопряженных направлений.
На практике оказалось, что метод ДФП может давать отрицательные шаги или окончиться в нестационарной точке. Это возможно, когда Hk+1 становится плохо обусловленной. Этого можно избежать путем увеличения числа получаемых значимых цифр или перезаданием матрицы Hk+1 в виде специальной диагональной матрицы H, где
.
Ошибки округления и особенно неточность линейного поиска может послужить причиной потери устойчивости метода ДФП и даже привести к ошибочным шагам, когда значение целевой функции на некоторой итерации возрастает вместо того, чтобы уменьшаться.
По классификации Ньютоновских методов данный алгоритм является квази-Ньютоновским, хотя он использует в явном виде только первые частные производные, а значит, может рассматриваться и как градиентный метод.
Практическая проверка эффективности алгоритма показала, что он столь же эффективен, как и метод Флетчера-Ривса.
dopoln.ru

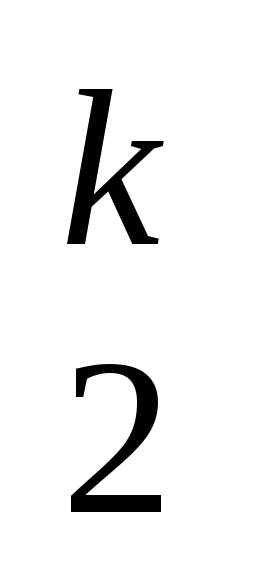
 )
)