4.5.3. Методы безусловной оптимизации. Безусловная оптимизация
Безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Безусловная оптимизация
Cтраница 1
Безусловная оптимизация: методы нулевого, первого и второго порядков; методы, использующие сопряженные направления. [1]
Безусловная оптимизация начинается с первого шага. [2]
Задачи безусловной оптимизации, которым мы уделили внимание в этом разделе, довольно редко встречаются в экономических исследованиях, основной особенностью которых является ограниченность используемых ресурсов. [3]
Методы безусловной оптимизации по способу определения направления поиска делятся на методы нулевого, первого и второго порядков. Для методов нулевого порядка типичен выбор направления поиска по результатам последовательных вычислений целевой функции. По способу выбора совокупности оптимизируемых параметров эти методы делятся на детерминированные и случайного поиска. [4]
Применение методов безусловной оптимизации, использующих производные, в ряде случаев затруднительно или нецелесообразно. Это относится к задачам оптимизации со многими переменными и с целевыми функциями сложного вида. Построение аналитических выражений для производных целевой функции в таких задачах может оказаться затруднительным либо вообще невозможным. Использование разностных схем выч исле-ния производных в этих случаях усложняет программирование, повышает затраты машинного времени и снижает точность решения. [5]
Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений. [6]
Для алгоритмов безусловной оптимизации функций общего вида построено довольно много тестовых задач, но даже в этом случае возникают некоторые из трудностей, описанных выше. Например, рассматриваются в основном задачи очень малой размерности; кроме того, не ясно, какие свойства алгоритмов проявляются на выбранных тестовых функциях. [7]
При применении методов безусловной оптимизации справедливо следующее: чем больше шаг вдоль направления, тем лучше. В том случае, когда первый уровень ( расчет схемы) является безытерационным ( з адача4), это справедливо и для многоуровневых процедур. В случае, когда первый уровень ( расчет схемы) является итерационным ( задача 1 для замкнутой схемы), это правило, вообще говоря, неверно. Действительно, при увеличении шага вдоль поискового направления действуют следующие противоположно направленные тенденции. С одной стороны увеличение шага вдоль направления дает хорошие результаты, поскольку уменьшается число итераций на втором уровне, но с другой стороны, увеличение шага ухудшает начальное пр иближение при решении системы ( I, 65), что может привести к уве-л ичению числа итераций на первом уровне. При очень большом шаге квазиньютоновский метод на этом уровне вообще может перестать сходиться. Должен существовать некоторый компромисс, при котором шаг вдоль направления будет наилучшим с точки зрения общего числа итераций на первом и втором уровнях. [8]
Для завершения обсуждения безусловной оптимизации мы докажем полезный ( хотя и простой) результат о том, что минимизация функции эквивалентна минимизации возрастающего преобразования этой функции. [9]
Используется какой-нибудь алгоритм безусловной оптимизации, например, метод градиента, усиленный привлечением идей метода сопряженных градиентов. Точка и используется, как начальная в этом процессе спуска. [10]
Среди прямых методов безусловной оптимизации один из наиболее эффективных - симплексный поиск, первоначально предложенный Спендли, Хекстом и Химсвортом. Основу метода составляет правило замены наихудшей вершины симплекса, которое заключается в следующем. В данном симплексе определяется вершина с наибольшим значением целевой функции. Она симметрично отображается относительно центра тяжести остальных п вершин. С полученным симплексом повторяется та же операция. Нелдер и Мид улучшили этот метод, дав иное правило определения новой вершины симплекса: вдоль прямой, проходящей через наихудшую вершину исходного симплекса и центр тяжести остальных вершин, кроме отражения, делаются дополнительные пробные шаги растяжения и сжатия для определения точки с меньшим значением целевой функции. [11]
Рассмотренные методы решения одномерной задачи безусловной оптимизации могут быть распространены и на многомерный случай. [12]
Исходную задачу приводим к задаче безусловной оптимизации. [13]
Наиболее многочисленную группу составляют методы безусловной оптимизации. Некоторое представление о широко применяемых методах этой группы дает рис. 3.2, В зависимости от порядка используемых производных целевой функции по управляемым параметрам методы безусловной оптимизации делят на методы нулевого, первого и второго порядков. [14]
Таким образом, для задачи безусловной оптимизации ( X Rn) теорема 1.2 не дает ничего нового в сравнении со знакомыми результатами ( теоремы 1.2 и 1.9 гл. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Метода - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Метода - безусловная оптимизация
Cтраница 1
Методы безусловной оптимизации по способу определения направления поиска делятся на методы нулевого, первого и второго порядков. Для методов нулевого порядка типичен выбор направления поиска по результатам последовательных вычислений целевой функции. По способу выбора совокупности оптимизируемых параметров эти методы делятся на детерминированные и случайного поиска. [1]
Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений. [2]
Наиболее многочисленную группу составляют методы безусловной оптимизации. Некоторое представление о широко применяемых методах этой группы дает рис. 3.2, В зависимости от порядка используемых производных целевой функции по управляемым параметрам методы безусловной оптимизации делят на методы нулевого, первого и второго порядков. [3]
Среди методов поиска локального экстремума методы безусловной оптимизации составляют наиболее многочисленную группу. [4]
Все рассмотренные ранее методы являются методами безусловной оптимизации. [5]
Для нейронных сетей хорошо работают многие методы безусловной оптимизации, часто лучше, чем узкоспециальные, придуманные для обучения нейронных сетей. [6]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра xt, на значения которого наложены ограничения, в неограничиваемый. [7]
В соответствии с делением экстремумов на условные и безусловные различают методы условной и безусловной оптимизации. Методы безусловной оптимизации могут быть применены к поиску условных экстремумов. Основным методом сведения задач условной оптимизации к безусловной является метод штрафных функций [49], та же цель достигается и при использовании мак-симинного критерия. В последнем случае каждое из ограничений на управляемые параметры представляется как условие работоспособности с соответствующим запасом. [8]
Совокупность методов НЛП, в зависимости от ограничений в математических моделях оптимизации, делится на две группы: методы безусловной оптимизации и методы условной оптимизации. Первые используют для решения задач без ограничений на оптимизируемые параметры, вторые - для задач с ограничениями. Следует отметить, что методы безусловной оптимизации ( см. описание методов штрафных функций) можно использовать и при решении задач с ограничениями, предварительно приведенных к задачам без ограничений. [9]
Если экстремум целевой функции отыскивается в неограниченной области X, то его называют безусловным экстремумом, а методы его поиска - методами безусловной оптимизации. [11]
Эта книга написана на основе трудов конференции по численным методам оптимизации при ограничениях, проходившей в Национальной физической лаборатории в январе 1974 г. Ей предшествовала конференция по методам безусловной оптимизации, проведенная тремя годами ранее. [12]
В соответствии с делением экстремумов на условные и безусловные различают методы условной и безусловной оптимизации. Методы безусловной оптимизации могут быть применены к поиску условных экстремумов. Основным методом сведения задач условной оптимизации к безусловной является метод штрафных функций [49], та же цель достигается и при использовании мак-симинного критерия. В последнем случае каждое из ограничений на управляемые параметры представляется как условие работоспособности с соответствующим запасом. [13]
Задача условной оптимизации (3.16) может быть сформулирована как задача безусловной оптимизации с помощью методов Лагранжа или штрафных функций. Тогда применяются методы безусловной оптимизации. [15]
Страницы: 1 2
www.ngpedia.ru
4.5.3. Методы безусловной оптимизации
Введем следующие обозначения: X[i,k] – вектор координатi-йвершины многогранника наk-мшаге поиска,i=1,2,…n+1,k=1,2,…;h – номер вершины, в которой значение целевой
функции максимально: f (X[h,k])= maxf (X[i,k]);l | – номер вер- | |
i |
|
|
шины, в которой значение целевой | функции | минимально: |
f (X[h,k])= minf (X[i,k]);X[n+2,k] – | центр тяжести всех вер- | |
i |
|
|
шин, за исключением X[h,k]. Координаты центра тяжести вычис-
| xj [n+ 2,k]= | 1 | n+1 |
|
|
ляют по формуле | ∑xj [i,k]− xj [h,k] | , j=1,2,…n. | |||
|
| n |
|
| |
|
|
| j=1 |
|
|
Примерный алгоритм метода деформируемого многогранника состоит в следующем:
1.Задаются коэффициентами отражения α, растяженияγ>1, сжатияβ<1, допустимой погрешностью определения координат
точки минимума ε. Выбирают координаты вершин исходного многогранникаX[i,k],i=1,2,…n+1,k=1.
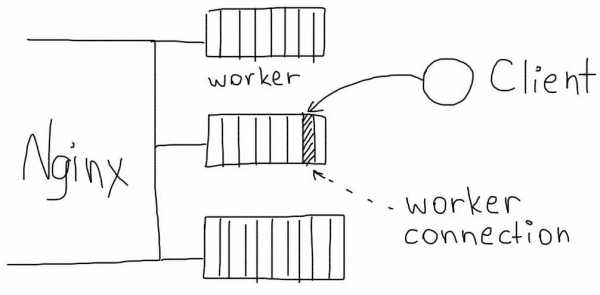
2.Вычисляют значения целевой функции во всех вершинах f(X[i,k]),i=1,2,…n+1, и находят точкиX[h,k],X[l,k] (на рис. 28,б точки соответственноX2 иX1), а такжеX[n+2,k].
3.Осуществляют проецирование точки X[h,k] через центр тя-
жести: X[n+3,k]=X[n+2,k]+α(X[n+2,k]–X[h,k]).
4.Если f(X[n+3,k])≤X[l,k], выполняют операцию растяже-
ния: X[n+4,k]=X[n+2,k]+γ(X[n+3,k]–X[n+2,k]).В противном случае переходят к п. 6.
5.Строят новый многогранник: если f(X[n+4,k])<X[l,k], то
заменой X[h,k] наX[n+4,k], в противном случае – заменойX[h,k] наX[n+3,k]. Продолжают вычисления с п. 2 приk=k+1.
6. Если X[h,k]>f(X[n+3,k])>X[i,k] для всехi, не равныхh,
выполняют операцию сжатия: X[n+5,k]=X[n+2,k]+β(X[h,k]–X[n+2,k]). Строят новый многогранник заменойX[h,k] наX[n+5,k] и продолжают вычисления с п. 2 приk=k+1.
7. Если f(X[n+3,k])>X[h,k], то, сохраняя вершинуX[l,k], строят новый многогранник, подобный текущему, уменьшением длин всех ребер в два раза:X[i,k]=X[l,k]+0,5(X[i,k]–X[l,k])и продолжают вычисления с п. 2 приk=k+1.
В пп. 6, 7 перед переходом к п. 2 необходима проверка выполнения условия завершения поиска минимума, например, по усло-
studfiles.net
Безусловная оптимизация - это... Что такое Безусловная оптимизация?
Безусловная оптимизация [unconditional optimization] - см. Оптимальная или оптимизационная задача.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- Безубыточность производства
- Безусловный минимум, безусловный максимум функции
Смотреть что такое "Безусловная оптимизация" в других словарях:
Оптимальная или оптимизационная задача — [optimization problem] экономико математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого то критерия) распределения наличных ресурсов. (Иногда то же: Экстремальная задача.) Решается с помощью оптимальной модели… … Экономико-математический словарь
оптимальная или оптимизационная задача — Экономико математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого то критерия) распределения наличных ресурсов. (Иногда то же: Экстремальная задача.) Решается с помощью оптимальной модели методами… … Справочник технического переводчика
Книги
- Лекции по математике. Том 7. Оптимизация, В. Босс. Книга охватывает классические разделы теории экстремальных задач: условная и безусловная оптимизация, выпуклые задачи, вариационное исчисление, принцип максимума, динамическое… Подробнее Купить за 571 грн (только Украина)
- Лекции по математике. Оптимизация. Том 7, В. Босс. Книга охватывает классические разделы теории экстремальных задач: условная и безусловная оптимизация, выпуклые задачи, вариационное исчисление, принцип максимума, динамическое… Подробнее Купить за 571 грн (только Украина)
- Лекции по математике. Том 7. Оптимизация, Босс В.. Книга охватывает классические разделы теории экстремальных задач: условная и безусловная оптимизация, выпуклые задачи, вариационное исчисление, принцип максимума, динамическое… Подробнее Купить за 467 руб
economic_mathematics.academic.ru
Безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 2
Безусловная оптимизация
Cтраница 2
Все рассмотренные ранее методы являются методами безусловной оптимизации. [16]
С помощью естественного обобщения получим задачу безусловной оптимизации, охватывающую весь блок ВПБ. [17]
Среди методов поиска локального экстремума методы безусловной оптимизации составляют наиболее многочисленную группу. [18]
Как правило, при решении задач безусловной оптимизации для достаточно гладких выпуклых или вогнутых функций F () методы, использующие первые и вторые производные, сходятся быстрее, чем методы нулевого порядка. Однако при оптимизации схем в условиях сложного непредсказуемого рельефа целевых функций F ( X), их алгоритмического, неявного способа задания, например посредством решения системы дифференциальных уравнений, а также при сложной форме ограничений использование методов нулевого порядка часто предпочтительнее. Кроме того, при неявном задании / 7 ( Х) ее производные приходится определять численно, а возникающие при этом ошибки, особенно в окрестности экстремума, создают значительные трудности для точного определения точки оптимума. [19]
Для нейронных сетей хорошо работают многие методы безусловной оптимизации, часто лучше, чем узкоспециальные, придуманные для обучения нейронных сетей. [20]
В этом случае мы говорим о задаче безусловной оптимизации. [21]
Квазиньютоновские методы являются эффективным средством решения задач безусловной оптимизации. Их отличает высокая скорость сходимости, в то же время при реализации квазиньютоновских алгоритмов не приходится выполнять такие трудоемкие операции, как вычисление матрицы вторых производных или обращение матрицы. Однако при большой размерности пространства необходимость хранения и пересчета на каждом шаге матриц Hk обусловливает высокие требования к объему занимаемой памяти ЭВМ. Этот недостаток не присущ изучаемому в следующем параграфе методу сопряженных градиентов. [22]
Задача поиска Е ( W) является задачей безусловной оптимизации. [23]
На рис. 12.12 приведены наиболее часто используемые методы безусловной оптимизации. [24]
В настоящем разделе рассматриваются аспекты практического применения методов безусловной оптимизации к обучению нейросетевых моделей. [26]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра xt, на значения которого наложены ограничения, в неограничиваемый. [27]
Теория необходимых и достаточных условий оптимальности в задачах безусловной оптимизации излагается в любом курсе математического анализа. [28]
Там же были приведены соответствующие результаты для задачи безусловной оптимизации и классической задачи на условный экстремум. В данной главе излагается общая теория необходимых и достаточных условий оптимальности в задачах математического программирования, включающая указанные результаты как частные случаи. [29]
Рассмотрим один из вариантов симплексного метода решения задачи безусловной оптимизации. [30]
Страницы: 1 2 3 4
www.ngpedia.ru
Задача - безусловная оптимизация - Большая Энциклопедия Нефти и Газа, статья, страница 1
Задача - безусловная оптимизация
Cтраница 1
Задачи безусловной оптимизации, которым мы уделили внимание в этом разделе, довольно редко встречаются в экономических исследованиях, основной особенностью которых является ограниченность используемых ресурсов. [1]
Таким образом, для задачи безусловной оптимизации ( X Rn) теорема 1.2 не дает ничего нового в сравнении со знакомыми результатами ( теоремы 1.2 и 1.9 гл. [2]
Исходную задачу приводим к задаче безусловной оптимизации. [3]
Как правило, при решении задач безусловной оптимизации для достаточно гладких выпуклых или вогнутых функций F () методы, использующие первые и вторые производные, сходятся быстрее, чем методы нулевого порядка. Однако при оптимизации схем в условиях сложного непредсказуемого рельефа целевых функций F ( X), их алгоритмического, неявного способа задания, например посредством решения системы дифференциальных уравнений, а также при сложной форме ограничений использование методов нулевого порядка часто предпочтительнее. Кроме того, при неявном задании / 7 ( Х) ее производные приходится определять численно, а возникающие при этом ошибки, особенно в окрестности экстремума, создают значительные трудности для точного определения точки оптимума. [4]
С помощью естественного обобщения получим задачу безусловной оптимизации, охватывающую весь блок ВПБ. [5]
Квазиньютоновские методы являются эффективным средством решения задач безусловной оптимизации. Их отличает высокая скорость сходимости, в то же время при реализации квазиньютоновских алгоритмов не приходится выполнять такие трудоемкие операции, как вычисление матрицы вторых производных или обращение матрицы. Однако при большой размерности пространства необходимость хранения и пересчета на каждом шаге матриц Hk обусловливает высокие требования к объему занимаемой памяти ЭВМ. Этот недостаток не присущ изучаемому в следующем параграфе методу сопряженных градиентов. [6]
В этом случае мы говорим о задаче безусловной оптимизации. [7]
Там же были приведены соответствующие результаты для задачи безусловной оптимизации и классической задачи на условный экстремум. В данной главе излагается общая теория необходимых и достаточных условий оптимальности в задачах математического программирования, включающая указанные результаты как частные случаи. [8]
Рассмотрим один из вариантов симплексного метода решения задачи безусловной оптимизации. [9]
Сведение исходной задачи условной оптимизации к последовательности задач безусловной оптимизации может быть выполнено с помощью функций штрафа. [10]
Задача поиска Е ( W) является задачей безусловной оптимизации. [11]
Теория необходимых и достаточных условий оптимальности в задачах безусловной оптимизации излагается в любом курсе математического анализа. [12]
Задача условной оптимизации (3.16) может быть сформулирована как задача безусловной оптимизации с помощью методов Лагранжа или штрафных функций. Тогда применяются методы безусловной оптимизации. [14]
Вообще задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на k подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить kK вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число k подобластей, что приводит к большим затратам машинного времени. [15]
Страницы: 1 2 3
www.ngpedia.ru
Безусловная одномерная оптимизация
Задачи безусловной одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:
.
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того минимизация функций одной переменной является как правило необходимым элементом многих методов минимизации многомерных функция безусловной и условной оптимизации.
На первый взгляд кажется, что задача минимизации функции одной переменной является довольно элементарной. В самом деле, если функция , которую нужно минимизировать на отрезке , дифференцируема, то достаточно найти нули производной, присоединить к ним концы отрезка, выделить из этих точек локальные минимумы и, наконец, среди последних найти ту точку, в которой достигается абсолютный минимум.
Однако для широкого класса функций эта задача не так уж проста. Во-первых, задача решения уравнения может оказаться, как это и бывает в отдельных ситуациях, весьма сложной. С другой стороны, в практических задачах часто не известно, является ли функция дифференцируемой. Ввиду этого существенное значение приобретают методы оптимизации не требующие вычисления производной.
Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений в заданных точках. Методами поиска определяется достаточно малый интервал, в котором находится минимум, осуществляя при этом наименьшее количество вычислений функции (так как затраты на вычисления могут быть весьма велики).
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Так как для приближенного определение точки оптимума исследуют поведение функции в конечном числе точек, то методы отличаются друг от друга лишь способом выбора этих точек. Суть методов состоит в построении последовательности отрезков стягивающихся к точке минимума.
Самым слабым требованием на функцию , позволяющим использовать эти методы, является ее унимодальность, то есть функция имеет на заданном отрезке только одну точку минимума. Прежде, чем применять эти методы, необходимо выделить интервал, содержащий искомую точку минимума, и убедиться, что она там единственная. В противном случае предлагаемые методы будут определять только один локальный минимум.
Похожие статьи:
poznayka.org