1.6 алгоритмы и методы безусловной оптимизации. Алгоритмы и методы безусловной оптимизации
1.6 алгоритмы и методы безусловной оптимизации. Психологическая интуиция искусственных нейронных сетей
Похожие главы из других работ:
Генетический алгоритм как метод оптимизации
1.1 Генетические алгоритмы и традиционные способы оптимизации
...
Градиентный метод первого порядка
Градиентные методы оптимизации
Градиентные методы оптимизации относятся к численным методам поискового типа. Они универсальны...
Задачи нелинейного программирования
2.2 Методы одномерной оптимизации
Задача поиска экстремума функции одной переменной возникает при оптимизации целевой функции, зависящей от одной скалярной переменной. Такие задачи входят составной частью во многие итерационные методы решения задач многомерной оптимизации...
Задачи нелинейного программирования
2.3 Методы многомерной оптимизации
В настоящее время разработано огромное число методов многомерной оптимизации, охватывающие почти все возможные случаи. Здесь рассматривается лишь несколько основных, считающихся классическими...
Метод расчета мехатронной системы привода телескопа на основе равновесно-оптимальной балансировки
2. Методы оптимизации ммс в условиях конфликта и неопределённости
...
Модели и методы конечномерной оптимизации
8. Сведение задачи условной оптимизации к безусловной задаче оптимизации.
...
Написание программы для удаления элементов и очистки внешних таблиц
2 МЕТОДЫ И АЛГОРИТМЫ
Внешние таблицы могут быть очень велики, поэтому для работы с ними принципиально неправильно использовать только оперативную память, необходимы различные дополнительные (вспомогательные) структуры, например файлы...
Оптимизация производства по выпуску продукции на предприятии Nature Republic
Раздел 2. Методы решения задачи многокритериальной оптимизации
Чтобы получить более полную характеристику достоинств и недостатков проектируемого объекта, нужно ввести больше критериев качества в рассмотрение. Как результат, задачи проектирования сложных систем всегда многокритериальные...
Основные методы решения задач нелинейного программирования
2.2 Методы одномерной оптимизации
Задача поиска экстремума функции одной переменной возникает при оптимизации целевой функции, зависящей от одной скалярной переменной. Такие задачи входят составной частью во многие итерационные методы решения задач многомерной оптимизации...
Основные методы решения задач нелинейного программирования
2.3 Методы многомерной оптимизации
В настоящее время разработано огромное число методов многомерной оптимизации, охватывающие почти все возможные случаи. Здесь рассматривается лишь несколько основных, считающихся классическими...
Профессиональная CAM-система трехмерного моделирования литейных процессов
2. Методы оптимизации
Методы условной оптимизации Вначале рассмотрим методы поиска min f (x1,…,xn) при условиях (2.1). Постановка задачи: Найти вектор, доставляющий минимум функции f (x1,x2,…,xn) при условиях, j=1,2,…,m. Другими словами, см. рисунок 2.20, требуется найти точку...
Разработка автоматизированных систем идентификации человека на основе биометрических признаков
1.2 Существующие алгоритмы и методы
...
Разработка автоматизированных систем идентификации человека на основе биометрических признаков
1.2.3 Алгоритмы и методы распознавания лиц
Задачи распознавания человека по изображению лица делятся на три больших класса: поиск в больших базах данных, контроль доступа и контроль фотографий в документах. Они различаются как по требованиям, предоставляемым к системам распознавания...
Разработка и исследование гибридного алгоритма решения сложных задач оптимизации
1.2 Алгоритмы целочисленной оптимизации
В силу того, что требуется решить задачу целочисленной оптимизации , где , необходимо привести основные термины и понятия данной теории и алгоритмы, которые используются в работе. Определение 1. S - область поиска оптимизации. В нашем случае...
Разработка интернет ресурса для магазина "Военная одежда"
2. Методы оптимизации
...
prog.bobrodobro.ru
Методы последовательной безусловной оптимизации
Основная идея методов условной оптимизации, использующих вспомогательные функции, состоит в преобразовании задачи вида:

к задаче вида:
,
где Р - вспомогательная функция,
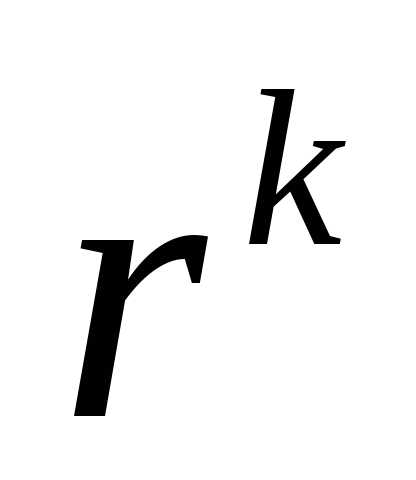 - параметр вспомогательной функции.
- параметр вспомогательной функции.
Штрафные функции
Штрафные функции – добавляемая к целевой функции функция 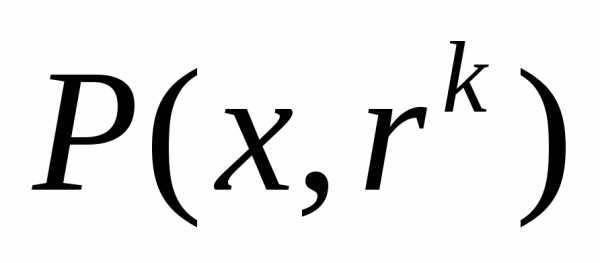 интерпретируется как штраф за нарушение каждого из ограничений. Штрафные функции конструируются, исходя из условий:
интерпретируется как штраф за нарушение каждого из ограничений. Штрафные функции конструируются, исходя из условий:
1. Квадратичный штраф используется для учета ограничений равенств:
2. Штраф типа квадрата срезки:
,
Где 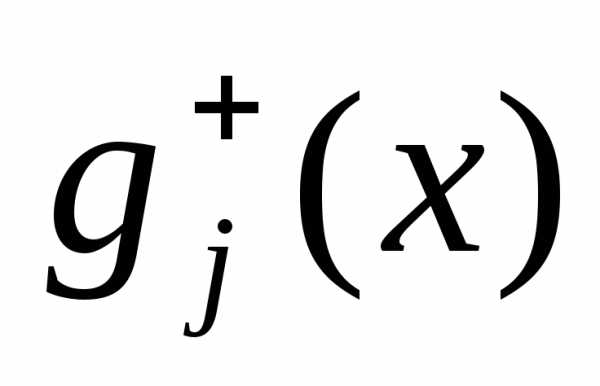 - срезка функции:
- срезка функции:
3. Бесконечный барьер является простейшим штрафом и используется в виде:
где  - множество индексов нарушенных ограничений.
- множество индексов нарушенных ограничений.
Барьерные функции
Барьерные функции – к целевой функции исходной задачи добавляется слагаемое, которое не позволяет генерируемым точкам выходить за пределы допустимой области.
1. Логарифмический штраф:
Логарифмическая штрафная барьерная функция неопределенна в недопустимых точках.
2. Штраф, заданный обратной функцией:
Является барьером и при нарушении ограничений теряет свои свойства.
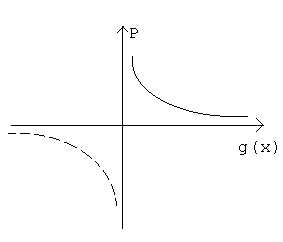
При использовании барьерных функций необходимо предусматривать вычислительные процедуры, в которых в случае нарушения ограничений происходит уменьшение шага поиска, поскольку при решении именно этой подзадачи возникают затруднения. Кроме того, необходимо учитывать условие итерационных процедур: .
Правила выбора параметра r
При использовании любой вспомогательной функции необходимо выбрать начальное значение 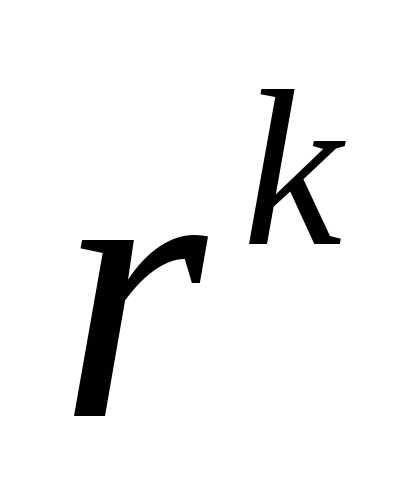 и изменять его после решения каждой подзадачи так, чтобы обеспечить сходимость последовательности точек {х(к)} к точке х*.
и изменять его после решения каждой подзадачи так, чтобы обеспечить сходимость последовательности точек {х(к)} к точке х*.
При использовании барьерных функций выбор начального значения  может оказаться важным с точки зрения сокращения числа итераций. Если начальное значение
может оказаться важным с точки зрения сокращения числа итераций. Если начальное значение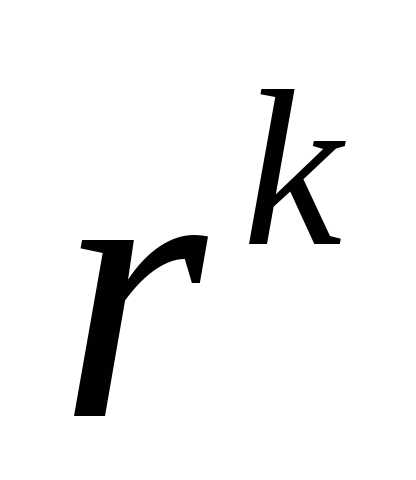 выбрано очень малым, то функцияzбудет мало отличаться отf(x) и метод будет сходиться быстро. Однако могут возникнуть осложнения из-за малой значимости штрафа. Слишком большое значение параметра
выбрано очень малым, то функцияzбудет мало отличаться отf(x) и метод будет сходиться быстро. Однако могут возникнуть осложнения из-за малой значимости штрафа. Слишком большое значение параметра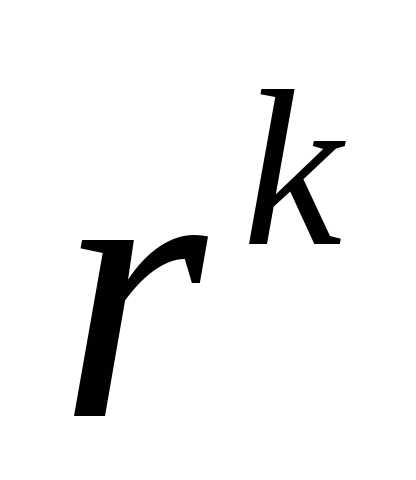 может привести к тому, что вспомогательная функция Р может стать доминирующей. Это может привести к большим вычислительным затратам. Для многих задач оптимальное значение параметра
может привести к тому, что вспомогательная функция Р может стать доминирующей. Это может привести к большим вычислительным затратам. Для многих задач оптимальное значение параметра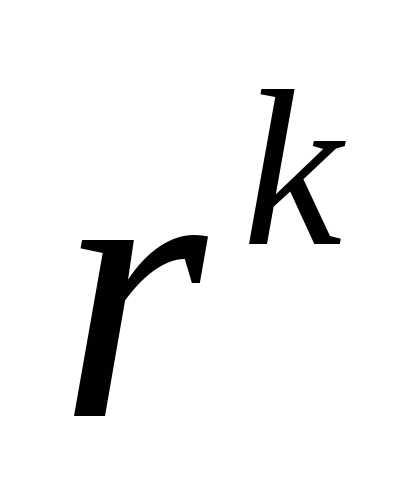 =1 (если
=1 (если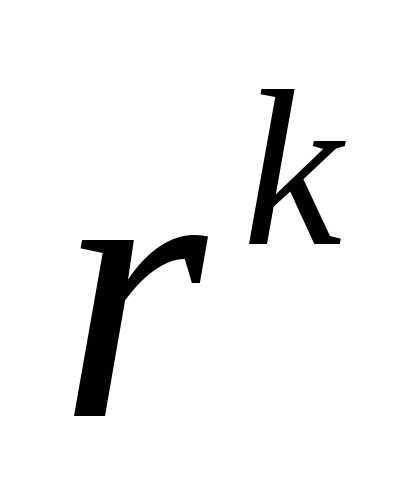 изменяется в сторону уменьшения).
изменяется в сторону уменьшения).
В зависимости от того, является ли х(к)на итерациях допустимой или недопустимой, методы условной оптимизации делятся на методы внутренней или внешней точки соответственно. Если последовательность из х(к)содержит точки обоих типов метод называется смешанным. Методы внутренней точки связывают с такими функциями Р, при которых стационарные точки функцииzоказываются заведомо допустимыми.
Общая модельная схема методов последовательной безусловной оптимизации
Шаг 1. Задать начальную точку 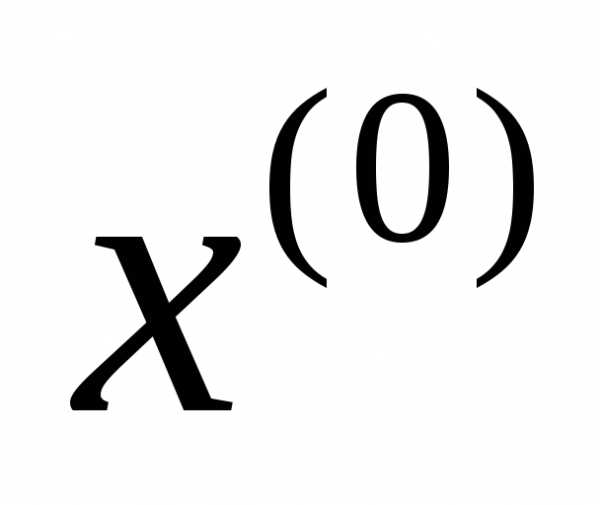 , начальное значение параметра штрафа
, начальное значение параметра штрафа , коэффициент
, коэффициент для изменения параметра, малые числа
для изменения параметра, малые числа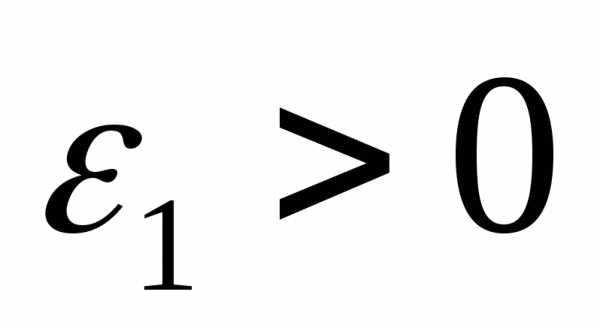 - параметр окончания процедуры безусловной оптимизации и
- параметр окончания процедуры безусловной оптимизации и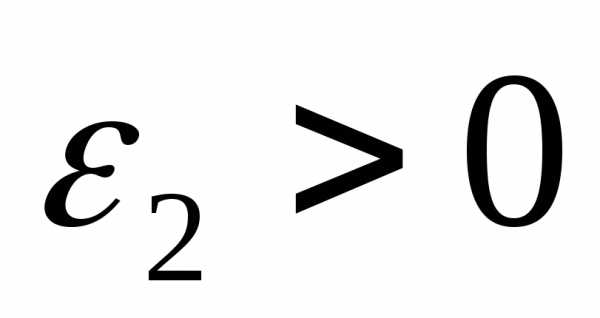 - параметр для остановки алгоритма,
- параметр для остановки алгоритма,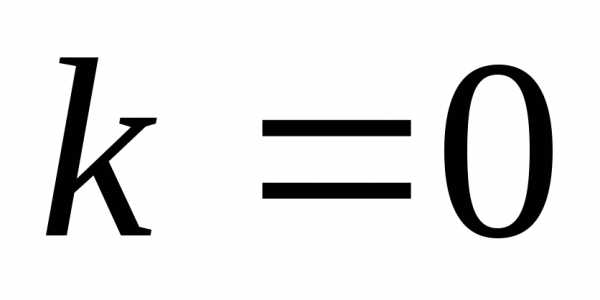 .
.
Шаг 2. Составить функцию 
Шаг 3. Найти точку 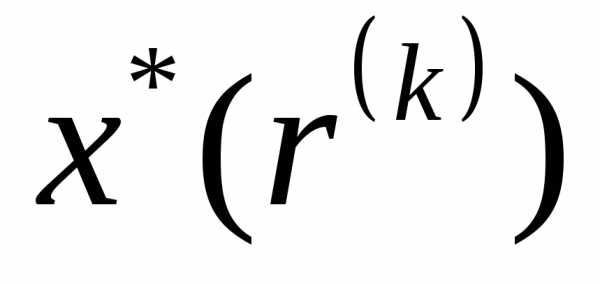 безусловного минимума функции
безусловного минимума функции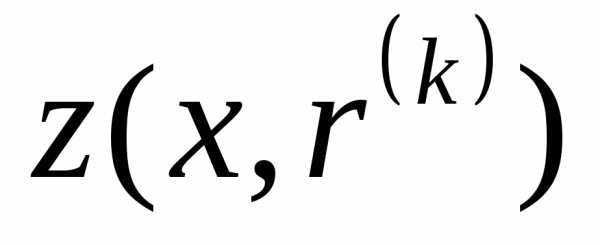 по
по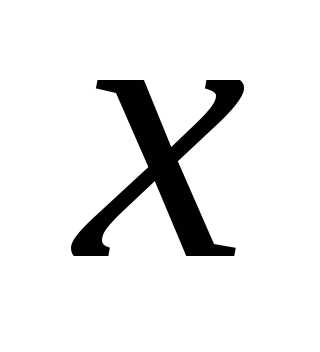 с помощью какого-либо метода. В качестве начальной точки взять
с помощью какого-либо метода. В качестве начальной точки взять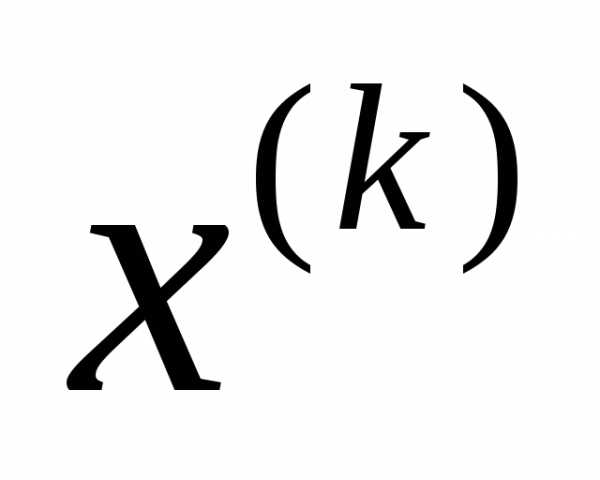 . Вычислить.
. Вычислить.
Шаг 4. Проверить условие окончания:
Если , процесс поиска завершить
Если , пересчитатьили
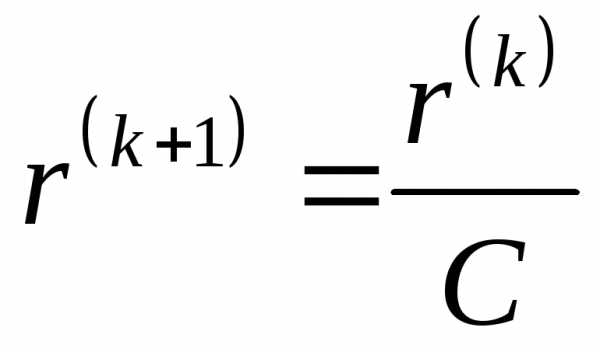 ,,и перейти к Шагу 2.
,,и перейти к Шагу 2.
studfiles.net
Метод безусловной оптимизаци - Энциклопедия по машиностроению XXL
Методы безусловной оптимизации. Для решения задачи безусловной оптимизации используют итерационные процессы вида [c.283]При описании комплексной целевой функции нелинейными зависимостями от внутренних параметров задача оптимизации решается методами линейного программирования если же целевая функция является линейной функцией от внутренних параметров, то имеет место задача линейного программирования. В общем случае целевая функция может иметь несколько экстремумов, отличающихся по абсолютной величине. В зависимости от типа экстремума, в котором заканчивается поиск оптимального решения, различают методы поиска локального и глобального экстремума. Если на значение определяемых параметров наложены некоторые ограничения, то решение задачи синтеза механизмов осуществляется методами условной оптимизации. В противном случае (при отсутствии ограничений) при синтезе механизмов для поиска значений определяемых параметров используют методы безусловной оптимизации. [c.316]
Среди методов поиска локального экстремума методы безусловной оптимизации составляют наиболее многочисленную группу. Сущность этих методов заключается в том, что строится такая последовательность значений вектора внутренних параметров х , Хц Х.2, при которой в случае поиска минимума целевой функции в [c.316]
Рис, 25.2. Обобщенный алгоритм методов безусловной оптимизации [c.317]
Методы безусловной оптимизации по способу определения направления поиска делятся на методы нулевого, первого и второго порядков. Для методов нулевого порядка типичен выбор направления поиска по результатам последовательных вычислений целевой функции. По способу выбора совокупности оптимизируемых параметров эти методы делятся на детерминированные и случайного поиска. В детерминированных методах процесс перехода от вектора внутренних параметров Х к вектору хс 1 происходит в [c.317]
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра XI, на значения которого наложены ограничения, в не-ограничиваемый. [c.319]
Метод безусловной оптимизации 316—319 [c.366]
Теперь поиск оптимального х проводится для функции F(x, q) с помощью любого метода безусловной оптимизации, например метода Ньютона. Для использования метода Ньютона (записи выражений) потребуется вычислить первые и вторые производные от функций X (х), ф (х), которые также можно выписать. [c.194]
Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений. [c.158]
Совокупность методов НЛП, в зависимости от ограничений в математических моделях оптимизации, делится на две группы методы безусловной оптимизации и методы условной оптимизации. Первые используют для решения задач без ограничений на оптимизируемые параметры, вторые — для задач с ограничениями. Следует отметить, что методы безусловной оптимизации (см. описание методов штрафных функций) можно использовать и при решении задач с ограничениями, предварительно приведенных к задачам без ограничений. [c.152]
Методы безусловной оптимизации, в свою очередь, делятся на методы, использующие производные, и методы, не использующие производных (методы поиска). К [c.152]
Применение методов безусловной оптимизации, использующих производные, в ряде случаев затруднительно или нецелесообразно. Это относится к задачам оптимизации со многими переменными и с целевыми функциями сложного вида. Построение аналитических выражений для производных целевой функции в таких задачах может оказаться затруднительным либо вообще невозможным. Использование разностных схем вычисления производных в этих случаях усложняет программирование, повышает затраты машинного времени и снижает точность решения. [c.156]
Для методов поисковой оптимизации типичен выбор направления поиска оптимума по результатам последовательных вычислений целевой функции. По способу выбора точки испытания целевой функции поисковые методы безусловной оптимизации делятся на детерминированные методы поиска и методы случайного поиска. В детерминированных методах процесс перехода из точки в точку происходит в соответствии с некото- [c.156]
Все рассмотренные ранее методы являются методами безусловной оптимизации. Следовательно, их применение к решению задач нелинейного программирования [c.157]
Методы безусловной оптимизации. Способ выбора направления поиска является определяющим для методов безусловной оптимизации, которые бывают нулевого, первого и второго порядков. В методах нулевого порядка для определения gk [c.71]
Методы условной оптимизации. Метод штрафных функций основан на преобразовании исходной задачи (3.3) с ограничениями к задаче без ограничений с применением к последней методов безусловной оптимизации. Преобразование проводится по формуле Ф(Х) =/ (Х)+0(Х), где Ф(Х) и F )—соответственно новая и первоначальная целевые функции, 0(Х) —функция штрафа, учитывающая нарушенные ограничения. В методе штрафных функций, называемом методом внешней точки, функция штрафа [c.75]
Методы расчета равновесного состава изложены в [33]. В работе [9] дано развитие этих методов, при этом рассмотрено два случая расчет равновесного состава при заданных давлении и температуре и расчет состава и температуры при заданных давлении и удельной энтальпии смеси. Показано, что оба случая сводятся к решению задачи безусловной минимизации выпуклых функций. Предложен алгоритм решения этих задач, основанный на применении численных методов безусловной оптимизации и сходящийся от любого начального приближения, что особенно важно при расчетах новых композиций и составов. [c.115]
Ограничения при оптимизации. До сих пор мы рассматривали задачу оптимизации во всем пространстве параметров, не накладывая никаких ограничений на возможные изменения параметров. Такая оптимизация называется безусловной. Часто решение, полученное методами безусловной оптимизации, не удовлетворяет требованиям конструктивной или физической реализуемости. [c.207]
Итак, для построения конкретного метода спуска мы имеем две задачи выбор направления Ах и спуск по направлению — выбор р . Главное отличие метода определяется выбором направления спуска. Для оптимизации оптических систем применяются преимущественно детерминированные методы. Стохастические или случайные методы, рассмотренные в работе [25], несмотря на свою простоту, не получили распространения из-за низкой сходимости. В следующих параграфах мы рассмотрим основные методы безусловной оптимизации, а затем коснемся задачи контроля ограничений. [c.216]
Производя затем оптимизацию с моделью (5.76) точно так же, как и с (5.23), одним из рассмотренных выше методов безусловной оптимизации, мы получим точку минимума в пространстве свободных параметров Ахз. Затем найдем связанные параметры Ах из формулы (5.75), обеспечивающей соблюдение ограничений. [c.244]
Формирование активного набора производится постепенно при помощи операций включения в набор и вывода из него. Будем полагать, что в начальной точке Хо данного шага ни одно из неравенств не нарушается, т. е. эта точка является допустимой. Методом безусловной оптимизации построим направление спуска из этой точки без учета ограничений. Если при движении по этому направлению ограничения не нарушаются, то контроль их не требуется. Пусть, спускаясь по построенному направлению из Хо, мы нарушили какое-либо неравенство. В этом случае остановимся на его границе в точке х и включим ограничение в активный набор в виде равенства. Используя формулы (5.80), от точки х будем двигаться с учетом этого ограничения, т. е. вдоль его границы. Если при этом движении нарушается еще одно неравенство, то останавливаемся на его границе в точке Хз, включаем его в набор и двигаемся далее по пересечению границ двух неравенств. Таким образом, движемся, пополняя активный набор. [c.246]
Задачи безусловной оптимизации, соответствующие случаю отсутствия ограничений в (5.26), образуют простой, но важный класс задач математического программирования. Помимо того, что такие задачи имеют широкое распространение, к ним с помощью различных способов могут сводиться более сложные задачи отыскания экстремумов на ограниченных множествах. Методы безусловной оптимизации разработаны достаточно хорошо, и для всех типов минимизируемых функций имеются удовлетворительные алгоритмы [96, 216]. [c.146]
Сформулируйте принципы прямых методов оценки направлений в задачах безусловной оптимизации. [c.329]
В математическом плане в работах по оптимизации параметров теплоэнергетических установок, выполненных в последние годы с использованием ЭЦВМ, наряду с современными методами нашли применение два старых метод вариантных расчетов с целью определения лучшего варианта из числа рассматриваемых и метод нахождения и приравнивания нулю частных производных величин приведенных расчетных затрат по оптимизируемым параметрам для получения экстремальной точки. Использование этих методов безусловно сузило возможности оптимизации теплоэнергетических установок. [c.6]
Суть метода заключается в преобразовании задачи условной оптимизации (4.19) в задачу безусловной оптимизации с помощью образования новой целевой функции [c.166]
Важная идея методов штрафных функций - преобразование задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции Ф(Х), за счет введения в исходную целевую функцию F(X) специальным образом выбранной функции штрафа S(X) [c.167]
Если ограничения на параметры модели отсутствуют, то для минимизации квадратичной формы (8 16) можно применять методы многомерной d> 1) или одномерной d = 1) безусловной оптимизации (см, пп. 5.1.10, 5.1.11 книги 1 настоящей справочной серии, а также [13, 19]). Если же ограничения на параметры существуют и их нужно учитывать, то следует использовать методы условной оптимизации [13]. [c.471]
Существенно отличается подход к решению задач с единственным и несколькими экстремумами. Во втором случае обычно требуется найти главный из них (так называемый глобальный). Наличие или отсутствие ограничений на искомые переменные относит задачу к области условной или безусловной оптимизации. В свою очередь линейность целевой функции или ограничений обуславливает использование методов линейного или нелинейного программирования. При постановке задачи существенное значение имеет то, что исходная информация не полностью определена и характеризуется определенными вероятностными свойствами. Такую задачу следует решать методами стохастического программирования. Наконец, подход к решению оптимизационной задачи значительно изменяется, если целевая функция приобретает не скалярный, а векторный вид. Тогда возникает необходимость оптимизации по нескольким независящим критериям. После этой краткой общей классификации остановимся более подробно на типах оптимизационных задач, наиболее подходящих для разработки приборов квантовой электроники. К таким задачам прежде всего относятся задачи параметрической оптимизации. [c.121]
При наличии нелинейных ограничений g, (х) О (t = 1, 2,. .., т) используются алгоритмы, в которых решение общей задачи нелинейного программирования сводится к решению задачи безусловной оптимизации градиентными методами. Для этого к целевой функции добавляется функция штрафа (С — вектор коэффициентов штрафа) [c.213]
Строго говоря, методы штрафных функций требуют многократного повторения всего процесса безусловной оптимизации с изменением коэффициентов г в формулах (5.69)—(5.72) таким образом, что г уменьшается на каждом /-м цикле оптимизации. Например [c.243]
В основу алгоритмов минимизации гладких функций на ограниченных множествах положены следующие идеи. Общая задача математического программирования может быть преобразована в задачу либо последовательность задач безусловной оптимизации. Такие алгоритмы основаны на использовании метода центров [225], замены независимых переменных [211], применении различных вариантов штрафных функций и модифицированных функций Лагранжа [215, 217, 218]. Можно отметить также метод [225], позволяющий перейти к безусловной минимизации функции максимума. Задача условной оптимизации может быть аппроксимирована последовательностью задач линейного или квадратичного программирования. К этой группе относятся методы возможных направлений [228], линеаризации [215], линейной аппроксимации [96], проектирования [218]. [c.148]
Рассмотрим необходимые и достаточные условия экстремума. Классические методы оптимизации используют тогда, когда известно аналитическое выражение функции Р (X) и известно, что она по крайней мере дважды дифференцируема по переменным проектирования. Тогда для определения экстремума используют необходимые и достаточные условия безусловного экстремума. Эти условия легко получить с помощью разложения f (X) в окрестностях экстремальной точки X в ряд Тейлора [c.278]
Методы поиска экстремума классифицируются по следующим признакам в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции — методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а в методах нулевого порядка производные не используют. [c.281]
Решение задачи связано с нахождением условного экстремума. Для нахождения безусловного экстремума задачу необходимо преобразовать так, чтобы она стала задачей на безусловный минимум. Это преобразование может осуществляться различными способами, выбор которых зависит от сложности и трудоемкости вычислений. Одним из эффективных способов является метод неопределенных множителей Лагранжа. Практические приемы преобразования и методы оптимизации решений достаточно подробно освещены в работах [21, 66]. [c.85]
В аналитических расчетах по оптимизации теплоэнергетических установок функционалы и ограничения упрощаются с целью получения относительно несложных аналитических зависимостей с ограниченным количеством переменных, что позволяет использовать классические методы исследования функций на экстремум — получение аналитических выражений производных по оптимизируемым переменным и приравнивание производных нулю, т. е. удовлетворение необходимых условий экстремума. Такой подход позволяет лишь получить безусловный экстремум при непрерывных переменных. [c.57]
Деннис Дж. мл., Шнабель Р. Численные методы безусловной оптимизации и решения нелинейных уравнений Пер. с англ. М. Мир, 1988. [c.477]
В соответствии с делением экстремумов на условные и безусловные различают методы условной и безусловной оптимизации. Методы безусловной оптимизации могут быть применены к поиску условных экстремумов. Основным методом сведения задач условной оптимизации к безусловной является метод штрафных функций [49], та же цель достигается и при использовании максиминного критерия. В последнем случае каждое из ограничений на управляемые параметры представляется как условие работоспособности с соответствующим запасом. [c.155]
Сходимость метода Ньютона гарантируется при условии выпуклости минимизируемой функции и ее непрерывной дифференци-руемости до второго порядка [218]. Величину а можно определить либо путем одномерной минимизации вдоль направления задаваемого (5.36), либо более просто в результате проверки соотношения givh+Pk 2Ч—g(vkXfiPkg i Vk) 2 , 0[c.148]
Вообщ,е задачи условной оптимизации более сложны, чем задачи безусловной оптимизации. Для их решения используют специально разработанные методы программирования с ограничениями. Одним из таких методов, которые относятся к методам поиска глобального экстремума, является метод сканирования, состоящий в том, что допустимая область поиска, определяемая системой ограничений, разбивается на к подобластей, в центре каждой из которых определяется значение целевой функции. Если целевая функция зависит от п параметров, необходимо выполнить вариантов расчета. Для надежного определения глобального минимума необходимо увеличивать число к подобластей, что приводит к большим затратам машинного времени. [c.319]
Методы решения задач оптимального проектирования 145 безусловной оптимизации 152 вариационного исчисления 147 геометрического программирования 157, 158 градиентные 153 динамического программирования 149 Дэвидона — Флетчера — Пауэлла 55 использующие производные 153 исследования функций классического анализа 145 линейного программирозания 151 множителей Лагранжа 146 наискорейшего спуска 153 не использующие производные 152, 156 нелинейного программирования 152 Ньютона 154 [c.216]
В ПМК оптимизации, используемых в САПР, методы и алгоритмы поиска обычно группируются в зависимости от постановки решаемого класса задач. Имеются группы методов безусловной, условной, дискретной оптимизации, центрирования и вписывания гиперфигур. [c.71]
Предварительно назначенные параметры кинематической схемы и обозначения элементов на топологии (рис. 24.2) приведены в табл. 24.1. Угловые положения элементов Ь6, Ь7 и Ь8 являются зависимыми от других параметров и вычисляются через них по тригонометрическим зависимостям. Вращение кривошипа механизма воспроизводится источником фазовой переменной типа потенциала (элемент Wl), в данном случае угловой скорости (см. рис. 24.2). Вывод результатов моделирования осуществляется индикаторами ПЕРЕМЕЩЕНИЕ ПОЛЗУНА и СКОРОСТЬ ПОЛЗУНА . Согласно результатам моделирования (рис. 24.3, а), максимальная скорость ползуна на этапе рабочего хода равна 0,542 м/с, минимальная - 0,425 м/с. Задачу корректировки параметров кинематической схемы можно поставить и решить как задачу безусловной оптимизации. Критериями оптимизации приняты максимальная скорость ползуна на участке рабочего хода и отклонение его полного хода от заданного. Целевую функцию формируют как аддитивный критерий со следующими весовыми коэффициентами при частных критериях 0,00001 для максимальной скорости ползуна на участке рабочего хода и 0,99999 для отклонения полного хода ползуна от заданного. В качестве параметров оптимизации принимают длины элементов кинематической схемы и их начальные угловые положения. Оптимизацию осуществляют методом Нелдера-Мида. Согласно результатам моделирования (рис. 24.3, б), максимальная скорость ползуна на этапе рабочего хода стала 0,416 м/с, что в 1,3 раза [c.505]
В целом можно сказать, что наиболее эффективными для задач безусловной оптимизации являются квазиньютоновские алгоритмы минимизации, относящиеся к группе методов первого порядка. Работа таких алгоритмов основана на аппроксимации гессиана Я(у) минимизируемой функции либо матрицы обратной, [c.147]
В зависимости от характера экст ремума различают методы условной и безусловной, а также локальной и оощей оптимизации. Наиболее удобно и просто реализовать на ЭВМ методы поиска безусловных локальных экстремумов. [c.30]
mash-xxl.info